基于FPGA的正余弦波发生器的CORDIC流水线设计❋

黄 俊

（合肥工业大学 仪器与光电工程学院，安徽 合肥 230009）

0 引言

有很多应用程序需要数字波形信号发生器，特别是在高精度测量领域，稳定的正余弦波的发生是一个研究热点。一个测量系统允许基于单一硬件平台执行许多函数，因此信号处理的高度可重构是必须的。CORDIC算法，也被称为Volder算法，首次应用在袖珍计算器上，目前也较为广泛地用于设计协处理器、建立离散傅里叶和余弦变换等数学处理上［1－4］。

1 CORDIC算法

CORDIC算法有两种操作，即向量和旋转模式。在向量模式中，坐标（x0，y0）旋转直到y0收敛到零；在旋转模式中，初始矢量（x0，y0）开始与x轴对齐，每一个周期旋转角度θi，所以n次迭代后获得角θn。旋转模式被用来近似正弦和余弦函数，其主要思想是采取一个一元向量连续旋转，直至达到所需的角度。这个旋转向量是一元的，所以当经过n次迭代之后将分别得到sinθn和cosθn，如果初始向量接近一固定值K，可以简化这个过程。将初始向量定义为v0＝（x0，y0），经过n次迭代后，向量（xn，yn）为：

在每个迭代中，向量执行一个微旋转θi，并得到新向量：

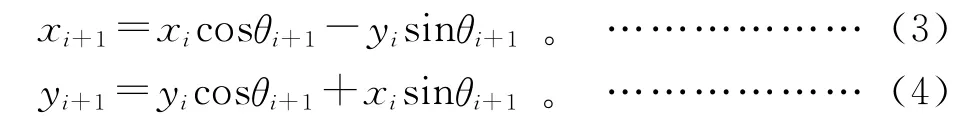
提取cosθi＋1，式（3）和式（4）可重新表述为：

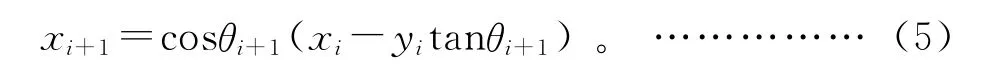
为了能够在硬件上方便实现，作如下约定：tanθi＋1的值为±2－i（其中i为整数）。所以基于此可将乘法运算转换成算术右移，且有cosθi＋1＝cos（arctan2－i），定义如下变量：

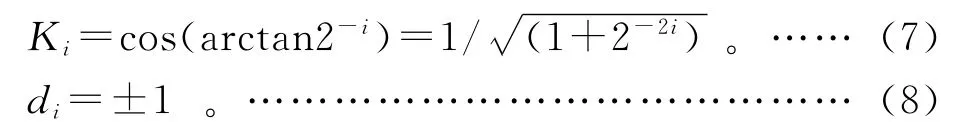
根据余弦函数的性质，cosα＝cos（－α）。所以式（5）、式（6）可以被转化成：

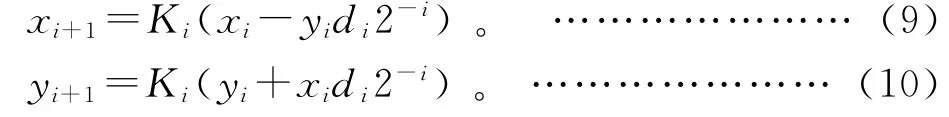
如果执行n次迭代，那么K的定义为每一个Ki连乘，即：

从式（9）和式（10）中可以看出，Ki可以被作为初始向量，v0＝（｜K｜，0）。微旋转与K补偿如图1所示，最后的n旋转，向量的长度为1，由于正余弦幅度值也为1，因此迭代之后可以将其看做是由正余弦部分组成。

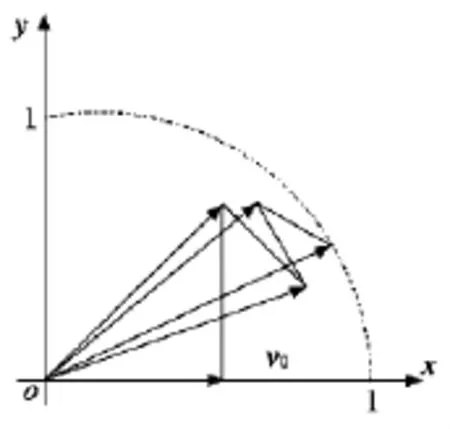
图1 微旋转与K补偿

作为向量初始化常数K，向量组件对于每次迭代都可简化为：

在每次迭代中需要决定di＝1或di＝－1。为了作出判断，考虑理想的角度和当前角度差异，所以定义一个新变量：

为了判断di的正负，使用下面的规则：

旋转角度之和为：可以预先计算arctan2－i来避免在FPGA中实现反正切函数。当i＝0时，20＝1，角度旋转的收敛范围在［－π／2，π／2］，初始值坐标为（1，0）。设置初始z值为所需要值，经过n级迭代后使得zn→0时，可以得到，从而实现正弦和余弦。

2 流水线架构

CORDIC的实现过程不需要从内存中调用正弦或者余弦值，而是通过一步步迭代来接近它的结果。在本文中，一个发生器需要连续计算正弦和余弦值，所设计的数字波发生器以CORDIC模块为核心。图2为CORDIC迭代，它主要由3个加法减法器和两个算术移位器构成，每个加法减法器关联到一个变量向量的分量和累积的角，记做x，y，z。在CORDIC的迭代实现过程中，对于相应的迭代，进程控制模块必须适应移位过程的要求。第一次迭代只有一个移位的变化，而第二次将会有两个或以上移位变化，图2中的j表示移位次数。

2．1 流水线化

CORDIC流水线操作的实现使用的是基本的CORDIC模块描述。流水线阶段开始之后，每个脉冲都会获得一个对应的输出，每个流水线阶段都会花费一个完整的脉冲来完成，如图3所示，在CORDIC流水线化整个过程中寄存器都将被使用到。

图2 CORDIC迭代

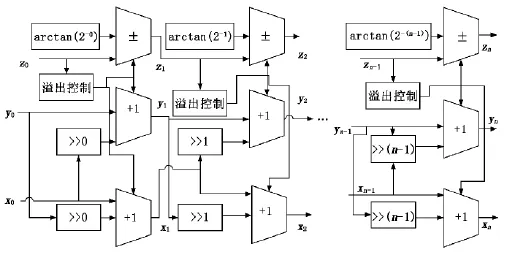
图3 CORDIC流水线

由于第一次迭代时旋转了arctan（20）＝45°，而旋转角度总和在－π／2～π／2之间，这就使得当所计算的角度绝对值大于π／2时，需要增加旋转。如要实现输出相位范围为－π～π，就需要对其采取相应变换。

2．2 角时序

CORDIC是给定一个角度来计算正弦和余弦的模块，因此有必要给它一个时序的CORDIC收敛的角度范围。它不是一个简单的序列的角度，必须能够由CORDIC改变频率信号。鉴于CORDIC只有收敛于第一和第四象限，这就需要角度从0到π／2，然后从π／2到－π／2，最后从－π／2到0变化。为解决此问题，需要构建一个锯齿波发生器，它从0开始，增加其输出值直到2n，一旦达到2n的信号，会从正最大值到最低负值，接着又会增加并且重复此循环。如图4所示，锯齿波需要变成一个三角波来适用于CORDIC模块，三角波必须存在于第一和第四象限之中。锯齿波的速度决定了正弦和余弦波的频率，事实上，与三角波相比，正弦和余弦波将会有相同的频率。

图4 锯齿波转化为三角波

在CORDIC的流水线设计中所使用的模块可在ALTERA系列中进行硬件语言（VHDL）描述，并且在ModelSim软件环境下进行模拟。可选用CycloneⅣGX系列EP4CGX22CF19C8芯片在QUARTUSⅡ软件中进行合成和实现架构，并测试其速度和优化面积。通过建立JTAG库来执行硬件联合仿真和绘制正弦和余弦波图形，合成后可以有效优化速度，以满足较高频率的需要。

3 结论

本文描述了一个基于CORDIC流水线架构的正弦和余弦波发生器。传统的生成数字正弦和余弦波的方法有多种，例如计算表法，但是这种方法需要过多的内存。相比于计算表法等方法，CORDIC算法不需要乘法或划分区块，而只需要加法减法器和移位寄存器，显示了较好的优越性，提供了一个非常好的替代选择，该算法能比较有效地应用于对低频率信号的处理上。

［1］ 李滔，韩秋月．基于流水线CORDIC算法的三角函数器［J］．电子技术应用，1999（6）：45－49．

［2］ 胡国荣，孙允恭．CORDIC算法及其应用［J］．信号处理，1991，12（5）：229－242．

［3］ 鞠建波，别庆，杜爱国．基于CORDIC算法的QDDS的实现及精度分析［J］．电视技术，2007，47（1）：112－116．

［4］ Javier Valls， Martin Kuhlmann， Keshab K Parhi．Evaluation of CORDIC algorithms for FPGA design［J］．Journal of VLSI Signal Processing，2002，32（3）：207－222．