基于空间网格的制导方法研究*
2013-09-02王芳刘新学王顺宏郭跃
王芳,刘新学,王顺宏,郭跃
(第二炮兵工程大学,陕西西安 710025)
0 引言
摄动制导是弹道导弹制导中广泛应用的方法之一,它以小偏差理论为基础,在主动段终点进行一阶泰勒展开,得到相应的关机方程。这种方法实施方便,对制导计算装置要求低,大量计算可放在发射前确定[1]。当出现大干扰时,摄动制导会产生较大的制导误差,而且误差会随着飞行时间和射程的增大而增加。为了改善摄动制导的缺点,能够修正大干扰对导弹的影响,弹道导弹常采用基于需要速度的闭路制导,并利用虚拟目标计算需要速度。由于虚拟目标确定时的简化,造成需要速度的计算偏差,引起制导方法误差[2-5]。为了解决这个问题,本文提出一种基于空间网格的制导方法(以下简称为“空间网格法”)。这种方法亦将大量计算放在射前准备阶段,同时具有弹上计算简单,数据存储量少,获取数据信息速度快,控制简单易实现的优点,而且能实时修正大干扰造成的偏差,具有广阔的研究和应用前景。
为了研究较为真实环境下空间网格法的可行性和规律性,文中假设地球为匀质旋转椭球体,考虑地球自转和扁率对弹道的影响。并在此假设条件下分析空间网格法的特点,检验这种新方法的可行性和适用性。
1 空间网格法概述
1.1 空间网格法的原理
简单地说,空间网格法就是在地面将导弹飞行可能经过的空间的速度值保存下来,当导弹飞到此空域时,将导弹当前速度以保存的速度为基准进行修正,直到导弹当前位置的当前速度与保存值相同时,控制导弹关机,即可命中目标。由于不可能将空间所有点的状态信息都记录下来,因此,将一定的空间区域通过一定划分原则,将其划分成网格状,仅保存网格节点处的状态信息,并以此为基准修正导弹的速度偏差。如图1所示,空间任意一点A,其速度矢量为v1,在此点的需要速度为v2,若不对速度偏差进行修正,经过时间t后飞至B点,但无法命中目标。若根据空间网格节点的速度对v1进行修正,当到达C点时达到关机条件,则关机后导弹可命中目标。
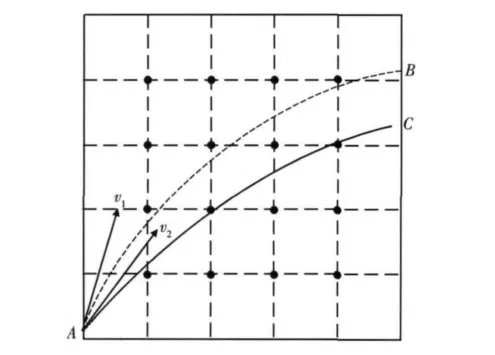
图1 空间网格法示意图Fig.1 Sketch map of space-gird method
通过以上分析可知,此方法的优点首先是脱离了小干扰理论,能修正大干扰对导弹造成的偏差;然后,大量计算在发射前就可准备完毕,计算速度快,弹上仅需实时获取与当前位置吻合的网格信息,并将其参与控制量计算,对导弹进行速度修正即可;最后,具有一定的命中精度,由于射前计算可以尽量使计算机仿真条件接近实际飞行条件,并将实际飞行时弹上无法实现的数值积分解算值保存到弹上作为控制基准,确保了命中精度。
同时注意到,如果仅在节点处才能获取网格信息并对导弹状态进行修正,网格的密度对飞行数据的修正将会有很大影响:一种可能是网格密度大,修正能力强,但存储量也随之增大,不利于计算速度,导致控制延时或失效;另一种可能是网格密度小,导弹并不能连续经过网格点,导致无法获取基准参数。因此,能否获取网格节点外的数据,对提高计算效率和该方法的可行性及适用性有很大关系,这也是本文研究的一个重要方面。下面首先对空间网格法的建立方法进行介绍,这也是对其可行性和适用性进行分析的前提条件。
1.2 空间网格的建立方法
建立一个空间网格,需要的基本元素有时间、速度、位置、网格范围和网格间距。其中,速度是基于其他元素通过弹道解算得到的导弹控制基准,是空间网格中最重要的元素。下面对它们逐个进行分析。
(1)基准坐标系的选择
1)时间基准
由于地球自转的影响,时间成为空间网格法必须考虑的因素。导弹当前点的时间应该与展开空间网格的中心点的时间一致,才能使用该网格数据,否则会造成结果偏差。可以将标准弹道上关机点附近某一时间点对应的位置为网格中心点Onet,其与标准弹道关机点时间之差为tnet,并以Onet为坐标原点在某个合适的坐标系下展开空间网格。依次类推,可以得到多组不同时间对应的空间网格,实际飞行时根据当前飞行时间选择不同的空间网格解算网格速度 vnet。
2)速度基准
由于弹上计算是以惯性空间为基准的,飞行状态参数为惯性系下的值。因此,网格中的速度参数为惯性系速度值,则可以直接与当前速度进行比较,提高计算速度。
3)位置基准
虽然导弹可能受到外界干扰的影响使导弹偏离标准弹道,但基本上都是在导弹飞行轨迹一定范围的管道内。若以惯性坐标系为基准,在标准弹道某一点附近展开空间网格,由于网格走向与弹道轨迹走向有较大差别,会有大量的网格数据失效,造成不必要的计算量和弹上存储空间的浪费。因此,以轨迹坐标系为基准,展开空间网格较为合理,可以更有效地发挥空间网格的作用。如图2所示惯性坐标系下的一段平面弹道,取其上某点为中心展开空间网格。虚线为以惯性坐标系为基准展开的空间网格边界;实线为以轨迹坐标系为基准,并将网格参数转换到惯性坐标系下的空间网格边界。通过对比可以看出,在轨迹坐标系下展开的空间网格的使用率更高,减小网格数据存储空间的浪费。
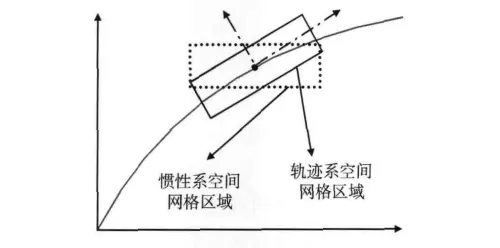
图2 不同坐标系下空间网格比较Fig.2 Comparison of space-grids in different coordinate systems
轨迹坐标系[6-9]定义为:取标准弹道关机点附近任意一点作为网格中心点Onet,并以此点为轨迹坐标系的原点Op;速度v方向为Opxp的指向;Opyp位于射击平面内,垂直于 Opxp,指向上方;Opzp与Opxp,Opyp构成右手直角坐标系。
发射坐标系[2-4]定义为:取发射点为原点O,Ox轴在发射点水平面内,指向发射瞄准方向,Oy轴垂直于Ox轴指向上方,Oz轴与Oxy平面垂直并构成右手直角坐标系。
因此,使用空间网格时需要将惯性系位置转换到轨迹坐标系方可使用。轨迹坐标系[p]与发射坐标系[g]间的关系矩阵为
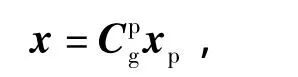
式中:
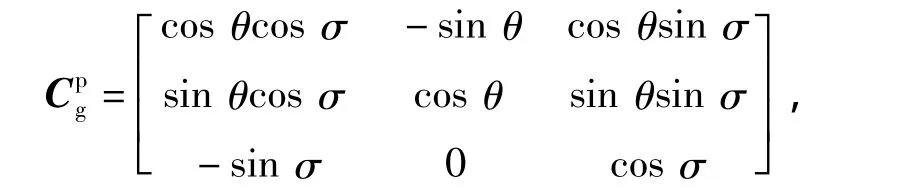
式中:θ为弹道倾角;σ为弹道偏角。
弹道倾角是导弹速度矢量v与水平面之间的夹角,若速度矢量v在水平面之上,弹道倾角为正,反之为负。弹道偏角为导弹速度矢量v在侧向平面上的投影与Ox轴之间的夹角。迎Oy轴顶视,若Ox轴逆时针转到投影线上,则σ为正,反之为负。再利用发射坐标系与惯性坐标系的转换矩阵,则可将弹上实时计算的惯性系位置转换到轨迹系下,再与空间网格数据对比,进而获取需要速度。
但是,需要注意的是,实际飞行轨迹与标准弹道不一定完全一致,导致当前点的弹道倾角和弹道偏角与展开空间网格的基准参数可能存在偏差,如果利用当前点的弹道倾角和弹道偏角将惯性系位置坐标转换到轨迹坐标系,必定产生轨迹坐标系与基准轨迹坐标系的偏差。为了解决这个问题,将基准轨迹坐标系与发射坐标系间转换矩阵的欧拉角保存到弹上,把当前惯性系位置转换到基准轨迹坐标系中,再获取需要的速度值。虽然基准轨迹与当前轨迹变化趋势有一定偏差,但仅产生网格边界的一些变化,不影响网格的使用。同时,由于网格节点的状态参数不受弹道倾角和弹道偏角变化的影响,因此该方法不会影响精度。
(2)网格范围和间距的选取
从导弹飞行特点来看,沿横向和法向的位置改变值相对纵向要小很多。如果空间网格的空域范围是正立方体,为了保证纵向距离满足要求,相应增加了不必要的横向和法向网格数据。因此,以轨迹坐标系为参考,将空间网格限定在纵向距离长,法向距离次之,横向距离最短的长方体区域,可以提高空间网格的利用率。网格范围Dgrid的确定与空间网格法的精度和外干扰影响有关。空间网格法在网格外围的精度决定网格的空域范围。同时,如果外干扰可能引起的导弹状态参数偏差超出网格边界,则弹体无法修正偏差,导致空间网格法失效。因此需要通过数学仿真,研究空间网格法的精度和外干扰的影响程度,从而确定网格范围。
此外,节点间距hnode的选择也很重要,这与节点之间的速度变化规律有密切联系。如果间距过大,造成不同节点的速度变化规律的扭曲,使节点参数精度不够,则需缩短节点距离以保证速度间的真实联系得以反映。如果间距过小,虽然节点速度间的规律得到更为精准的描述,但是数据量大,占用存储空间多,计算缓慢,也是不可取的。因此,需要通过仿真试验,根据节点之间速度的变化规律和对空间位置的敏感程度,才能确定网格间距。
(3)节点速度的确定
节点速度vnet求解是空间网格法的重点和难点。根据椭圆弹道理论,经过空间任意两点间的椭圆有无数个,因此从空间任意一点有无数个速度矢量使其通过目标点。因此,必须对速度设置限制条件,从而确定当前点到目标点的轨迹,不然无法确定网格节点速度。同时,需要规定速度的搜索顺序和搜索原则,使速度变化有一定规律可循。否则节点间没有任何联系,导致空间网格法失效。vnet的求解思路如下:
仅通过改变一个方向的速度来同时调整纵、横向偏差难以实现,至少需要同时改变2个方向的速度才能将纵、横向偏差修正到要求范围内。如果同时改变3个方向速度来修正纵、横向偏差,由于速度组合太多,调整原则不好把握,可操作性差。因此,可以采用固定某一方向速度,设该速度用vconst表示,其他2个方向速度可变,用valter表示,通过解算弹道得到落点偏差,以先改变速度值大者,再改变速度小者,先修正纵向偏差ΔL,再修正横向偏差ΔH为原则,得到满足精度要求的网格速度。若假设vx一定,vy>vz,通过弹道解算,得到节点速度;依次类推,改变vconst的大小,再重复迭代弹道[10-11],解算落点偏差[12],得到节点相应其他2个方向的速度。于是可以得到同一网格节点的多组不同速度组合,在使用时可以根据实际需要选择当前位置的需要速度,节点速度的求解过程如图3所示。
根据以上分析,空间网格法是在不同时间、不同节点位置基础上得到能命中目标的多组节点速度的一种离散化方法。该方法能够准确计算需要速度,但是计算产生大量数据给弹上存储和计算带来一定难度。因此,空间网格不同节点的速度之间是否相互联系,不同时间对应的空间网格节点速度是否有规律可循,成为该方法能否进一步简化,是否能得到准确的网格速度,以及进一步提高计算速度的重要环节。
2 空间网格法的规律性分析
初始条件:以弹道A的关机点为网格中心点Onet,飞行时间为 tnet;网格范围 Dgrid,Opxp方向(-100 000,100 000)m,Opyp方向 (-15 000,15 000)m,Opzp方向(-3 000,3 000)m;节点间距hnode,Opxp方向4 000 m,Opyp方向1 000 m,Opzp方向1 000 m。假设vconst=vx,通过调整vy和 vz修正ΔL和ΔH。
根据以上条件分析如下3种情况时,vnet在空间网格中的变化情况。
(1)tnet相同,vconst唯一
这是在空间网格中对速度以外的其他元素都加以限定所建立的网格。此条件下的空间网格是空间网格法中的基础网格,空间网格法是由多个基础网格组成的。本小节主要是分析在仅划分出一个空间网格时,valter的变化规律。
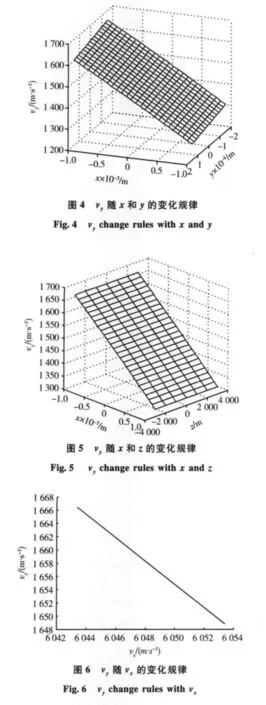
图4,5分别给出vy随x和y,vy随x和z的变化规律,可以看出vy与x,y和vy与x,z均近似成双线性关系。即vy与节点位置近似成线性关系。
(2)tnet相同,vconst变化
在(1)的基础上,如果vconst=vx变化,则得到同一节点处,相同空间网格的不同vnet=vy。图6给出了vy随vx的变化关系,图中显示vy与vx也满足线性关系。
(3)tnet变化,vconst唯一
由于飞行时间对落点有影响,因此必须分析当tnet不同时的情况。如图7所示的vy在不同tnet条件下的变化趋势。可以看出vy与tnet近似成线性关系。
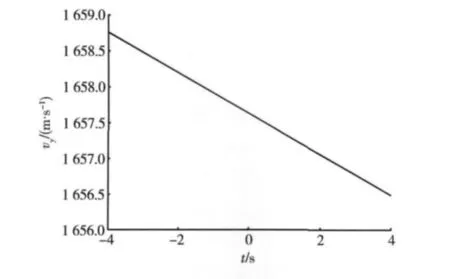
图7 vy随tnet的变化规律Fig.7 vychange rules with tnet
tnet变化,vconst变化时vy的变化规律是情况(2),(3)叠加时vy随tnet和vconst的变化规律,这里不再给出示意图。由于vy与vconst满足线性关系,vy与tnet也近似成线性关系,则tnet和vconst同时变化对vy的影响,与情况(1)中分析的结果类似,即vy与tnet,vconst成双线性关系。
以上给出了 vy随 t,x,y,z,vconst的变化规律,vz的变化情况与之类似,这里不再具体分析。通过以上分析,可以看出空间网格法中valter的变化是有规律可循的。层层的线性关系构成空间的多维网格,当给定 t,x,y,z,vconst时,可以通过线性插值得到valter,从而确定需要速度。但是这种线性程度是否满足精度需要,必须加以分析才能确定空间网格法是否具有使用价值。
3 空间网格法的可实现性分析
通过第 2 节的分析,valter与 t,x,y,z,vconst近似成线性关系。但是线性程度的好坏直接影响导弹当前位置需要速度的精度,能否通过线性插值或其他拟合方法得到符合精度要求的节点速度vnet是空间网格法得以使用的重要依据。利用与第2节相同的初始条件和仿真得到的空间网格数据,对空间网格法的线性程度进行分析。
分析方法是假设空间网格法符合多维线性关系,利用线性插值得到节点以外空间点的运动参数,并以此为关机点参数解算被动段弹道,计算落点偏差是否满足精度要求。如果满足要求,则空间网格法的线性程度好,网格数据规律性强,可以作为控制导弹运动的基准参数。如果不满足要求,而其他曲线拟合函数也无法满足要求,则网格数据的波动起伏较大,仅存在局部线性关系,则限制了该方法的使用。
仍以vconst=vx为例,按照第2节给出的几种情况分别对节点以外空间点的精度进行分析。
(1)vx和 t不变时,假设 vx=6 048,t=0。vy,vz分别与x,y,z的线性程度分析如表1和表2所示。表中随机给出多组x,y,z,通过三次线性插值得到对应的vy,vz,并计算落点偏差ΔL和ΔH。可以看出,如果导弹当前飞行时间和vx可以从保存的网格数据中找到,而位置不是保存的节点位置,通过插值得到的需要速度分量,使落点偏差基本上在1 m以内,满足精度要求。

表1 位置偏差仿真结果1Table 1 Simulation results of position deviation1

表2 位置偏差仿真结果2Table 2 Simulation results of position deviation2
(2)x,y,z,vx不变时,假设 x=10 450,y=1 380,z=720,vx=6 050。vy,vz与 t的线性程度分析如表3所示。表中随机给出多组t,线性插值得到对应的vy,vz,以及落点偏差ΔL和ΔH。表中数据显示通过时间插值得到的需要速度分量,保证了落点精度,验证了vy,vz与t具有良好的线性关系。
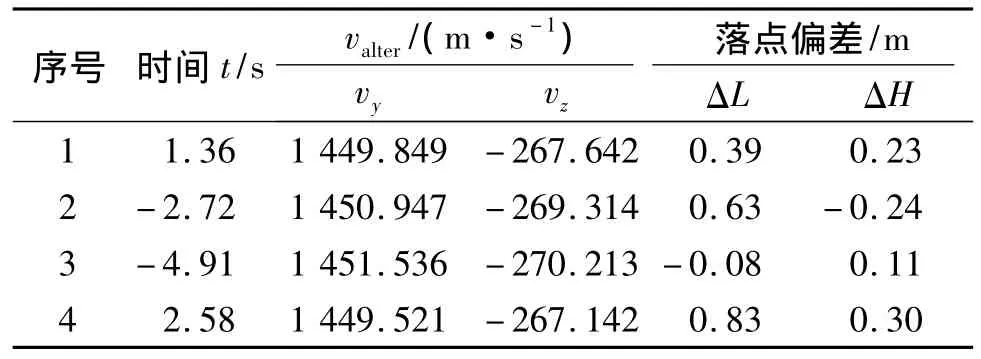
表3 时间偏差仿真结果Table 3 Simulation results of time deviation
(3)x,y,z,t不变时,假设 x=96 000,y=14 000,z=-3 000,t=0。vy,vz与 vx的线性程度分析如表4所示。表中随机给出多组vx,线性插值得到对应的vy,vz,以及落点偏差ΔL和ΔH。表中落点偏差在1 m以内,证明vy,vz分别与vx的线性关系。
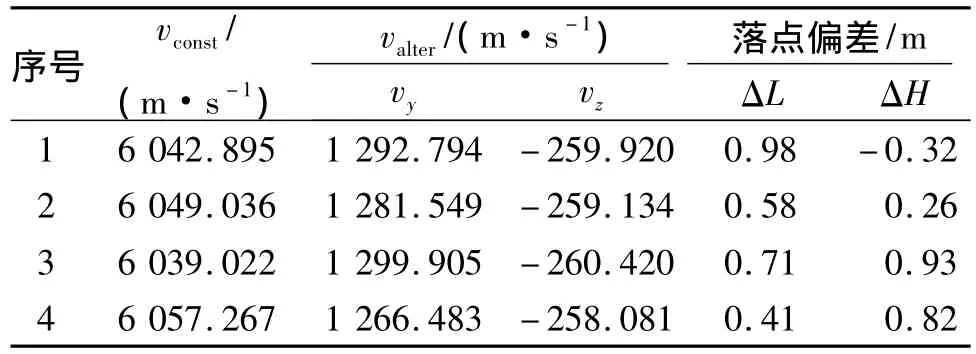
表4 速度vx偏差仿真结果Table 4 Simulation results of vxdeviation
从以上分析可以看出 valter与 t,x,y,z,vconst的线性程度很高,落点精度基本保证在1 m以内,满足精度要求。当 t,x,y,z,vconst与节点参数不吻合时,通过层层的线性插值得到valter,进而得到需要速度。但是,空间网格法需要进行大量的计算,增加了弹上存储负担。为了在保证精度的前提下减小数据存储量,需要通过仿真确定合适的网格距离和其他网格元素的步长。另一方面,由于良好的线性关系,如果利用线性拟合公式表示 valter与 t,x,y,z,vconst的关系,仅保存方程系数,可以大大减小存储空间。
4 结束语
基于空间网格的制导方法是在摄动制导方法基础上,为了增强导弹应对大干扰偏差的能力而提出的一种新方法。利用空间网格法参与制导运算,使得制导精度、抗干扰能力以及自适应能力方面均优于摄动制导,同时具有摄动制导中控制参量可以预先计算和装订,实时计算量小的优点。空间网格法计算简单,速度快,精度高,具备在弹上制导计算中应用的条件;并且它将大量工作放在射前计算,弹上运算速度快,控制简单,易操作。因此,空间网格法具有一定的发展前景,它的应用为导弹抵抗外干扰,提高弹上计算速度探索了一条新的途径。
[1] 马瑞萍,肖凡,张涛.一种基于速度倾角的闭路制导方法[J].航天控制,2012,30(1):6-9.MA Rui-ping,XIAO Fan,ZHANG Tao.A Close-Loop Guidance Based on Velocity Dip Angle[J].Aerospace Control,2012,30(1):6-9.
[2] 王继平,王明海,杨建明.一种新的闭路制导导引方法[J].航天控制,2007,25(5):58-61.WANG Ji-ping,WANG Ming-hai,YANG Jian-ming.A New Guided Method of Close-loop Guidance[J].Aerospace Control,2007,25(5):58-61.
[3] 廖洪昌,陈奇昌,王明海,等.远程弹道导弹闭路制导方法建模与仿真[J].弹箭与制导学报,2006,26(2):363-366.LIAO Hong-chang,CHEN Qi-chang,WANG Ming-hai,et al.Modeling and Simulation of Closed-loop Guidance Method of Long Range’s Ballistic Missile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(2):363-366.
[4] 王继平,王明海.一种基于标准弹道点的制导方法[J].上海航天,2008(1):16-20.WANG Ji-ping,WANG Ming-hai.A Guidance Method Based on Standard Ballistic Point[J].Aerospace Shanghai,2008(1):16-20.
[5] 康建斌,赵久奋,赵建亭,等.虚拟再入点摄动制导方案应用研究[J].航天控制,2005,23(3):20-25.KANG Jian-bin,ZHAO Jiu-fen,ZHAO Jian-ting,et al.Research on a New Virtual Reentry Point Perturbation Scheme[J].Aerospace Control,2005,23(3):20-25.
[6] 肖龙旭.地地导弹弹道与制导[M].北京:中国宇航出版社,2003.XIAO Long-xu. BallisticTrajectoryand Guideof Ground-to-Ground Missile[M].Beijing:The Astronomic Press,2003.
[7] 张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,1999.ZHANG Yi,XIAO Long-xu,WANG Shun-hong.Ballistics of Ballistic Missile[M].Changsha:National University of Defense Technology Press,1999.
[8] 肖龙旭,王顺宏,魏诗卉.地地弹道导弹制导技术与命中精度[M].北京:国防工业出版社,2009.XIAO Long-xu,WANG Shun-hong,WEI Shi-hui.Guidance Technology and Hit Accuracy of Ballistic Missile[M].Beijing:National Defense Industry Press,2009.
[9] 赵汉元.飞行器再入动力学与制导[M].长沙:国防科技大学出版社,1997.ZHAO Han-yuan.Dynamics and Guidance of Reentry Vehicles[M].Changsha:National University of Defense Technology Press,1997.
[10] 马丹山,王明海,车明波.弹道导弹的标准弹道迭代方法研究[J].飞行力学,2007,25(4):48-49.MA Dan-shan,WANG Ming-hai,CHE Ming-bo.Study on Iteration of the Ballistic Missile's Standard Trajectory[J].Flight Dynamics,2007,25(4):48-49.
[11] 王海丽,陈磊,胡小平.弹道导弹基本诸元的快速装订算法研究[J].国防科技大学学报,1999,21(2):5-8.WANG Hai-li,CHEN Lei,HU Xiao-ping.Research of Efficient Method for Computing Basic Firing Data of Ballistic Missiels[J].Journal of National University of Defense Technology,1999,21(2):5-8.
[12] 熊介.椭球大地测量学[M].北京:解放军出版社,1988.XIONG Jie.Ellipsoidal Geodesy[M].Beijing:Liberation Army Press,1988.
