基于临界寿命曲线的在役桥梁剩余寿命预测方法

季国伟 徐世伟

(1.山东省潍坊市公路管理局，山东潍坊 261061;2.山东宏昌路桥集团工程有限公司，山东潍坊 261061)

0 引言

随着在役公路桥梁服役年限的增加，混凝土结构会遭受不同程度的侵蚀、损伤，结构的可靠度也随服役时间延长而降低。因此，准确界定桥梁在使用过程中的安全性以及安全使用寿命具有十分重要的意义，而在役桥梁结构承载力剩余使用寿命预测技术，无疑是解决这一矛盾的有力手段。本文将结合某锈蚀钢筋混凝土空心板桥的受弯承载能力试验结果，运用相应的统计参数，建立受弯构件承载能力临界寿命曲线，并由此验证所提方法的工程实用性。

1 临界寿命曲线的可靠性分析方法

1.1 临界寿命曲线的理论基础

在役桥梁结构可靠度分析涉及到较为复杂的“全随机过程”模型，应用起来极不方便。参照桥梁结构可靠度的一次二阶矩阵分析方法，在役桥梁结构功能函数的各基本变量也采用随机变量的形式，据此构造在役桥梁结构的功能函数。

对于新建结构而言，由于结构恒载G和汽车荷载Q是公路桥梁最主要的荷载类型，若结构的抗力随机变量为R，相应的荷载效应随机变量为SG，SQ，则桥梁结构的极限状态方程可表示为［7］:

其中，SQ为采用设计基准期T0内最大荷载效应随机变量，且SQ服从极值Ⅰ型分布，恒载效应SG服从正态分布，抗力R服从对数正态分布。

对于在役桥梁结构，应考虑拟服役基准期T及抗力衰减等因素的影响。若抗力属简单随机过程模型，即任一时刻的抗力可用某一确定性函数k(T)修正，则相应的结构功能函数可表示为:

其中，k(T)为考虑抗力折减因素的抗力修正系数;SQT为与拟服役基准期T对应的最大活载效应随机变量。

根据式(2)，对于任一给定的拟服役基准期T及活载效应SQT，必然存在一个特定的k(T)，使结构满足最低可靠指标限值的要求。对于某一桥梁结构或构件，若已知初始抗力、恒载效应以及汽车荷载效应的概率模型，即可建立相应的k—T关系曲线，该曲线即为与不同拟服役基准期对应的抗力折减系数限值或临界寿命曲线。若已知结构或构件的抗力衰减曲线，其与临界寿命曲线的交点对应的T即为结构的临界寿命，减去已服役时间即为结构的剩余使用寿命。

已有的结构剩余寿命预测分析中，首先拟定结构的最低可靠指标限值，然后根据结构抗力衰减模型与荷载效应概率模型，计算与不同拟服役时间对应的可靠指标β(T)，建立β—T关系曲线，然后根据β—T曲线与β=［β］的交点确定拟服役时间。

分析以上预测方法可以看出，临界寿命曲线是结构承载能力寿命准则的另一表达方式，其理论基础与按最低可靠指标限值的分析方法是完全相同的，从工程实用角度，采用临界寿命曲线可避免复杂的可靠指标计算过程，便于工程技术人员使用。

1.2 临界寿命准则

由于结构动态可靠度或可靠指标β(t)是结构服役时间的函数，因此如何确定最低可靠指标是承载能力寿命预测的重要前提。迄今为止，对于最低可靠指标的如何取值存有争议，主要集中在按0.85β0取值或按目标可靠指标β0下降0.5取值等两种寿命准则［4，7］。若按0.85β0取值，对于在役桥梁结构或构件，发生破坏的一级、二级、三级构件，其最低可靠指标分别为0.705，0.63，0.555，最小值接近 0.5。其中，β0为 GB/T 50283-1999 公路工程结构可靠度设计统一标准规定的目标可靠指标。

2 抗力衰减函数模型分析

结构抗力随时间的变化属非平稳随机过程［12-14］。为简化计算，假设钢筋混凝土结构的抗力分布概型不随时间变化，构件抗力的简单随机过程模型［7，14］表述如下:

其中，φ(t)为结构抗力衰减函数，与结构的组成材料、环境等因素以及维护条件等有关，可以根据结构在已服役期间的材料性能变化规律、环境因素等综合确定;假定在t时刻抗力的变化基于初始抗力R0的随机性，则t时刻R(t)概率分布类型不变，其平均值和变异系数为:

假定初始抗力按照设计采用的抗力函数计算，即μR0=κR·Rk，代入式(4)可得:

其中，Rk为按规范规定的材料性能和几何参数标准值用抗力计算公式求得的构件抗力值，即Rk=R(fki·aki);κR为设计抗力R参数，按规范取用［15］;Rk(t)为t时刻抗力折减后的值。

由式(4)和式(5)可知，对评估基准期内的构件进行可靠性计算时，可采用规范采用的抗力统计参数，而不同时刻抗力变量的折减可视为初始抗力标准值的折减。

对于锈蚀钢筋混凝土受弯构件而言，根据文献［7］，抗力衰减函数φ(t)可取为:

其中，η(t)为钢筋截面面积随时间的锈蚀率;ξ为钢筋直径的腐蚀率，且ξ=Δd/d，Δd为钢筋直径的腐蚀速度。

显然，对于由钢筋锈蚀导致的受弯构件抗力衰减与承载能力寿命预测分析，可采用式(6)给出的抗力衰减函数。

3 荷载效应概率模型

3.1 恒载效应

对于在役桥梁而言，恒荷载效应服从正态分布，其统计参数为:

3.2 汽车荷载效应

为简化动态可靠度计算过程，可采用评估基准期内最大荷载效应概率模型进行分析［5，7］，即在役桥梁的汽车荷载效应最大值仍服从极值Ⅰ型分布，且与桥梁的继续使用期或剩余寿命有关，其分布函数和统计参数可根据实测资料或现行规范进行推算。

基于以上分析，在已有结构的评估基准期T1内，荷载效应最大值SQT1的概率分布函数FSQT1(x)及其统计参数可根据下式推求:

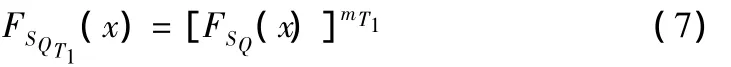
由此即可根据现行规范推求不同评估基准期相对应的汽车荷载产生的弯矩效应最大值概率分布函数与统计参数［15］，见表1。

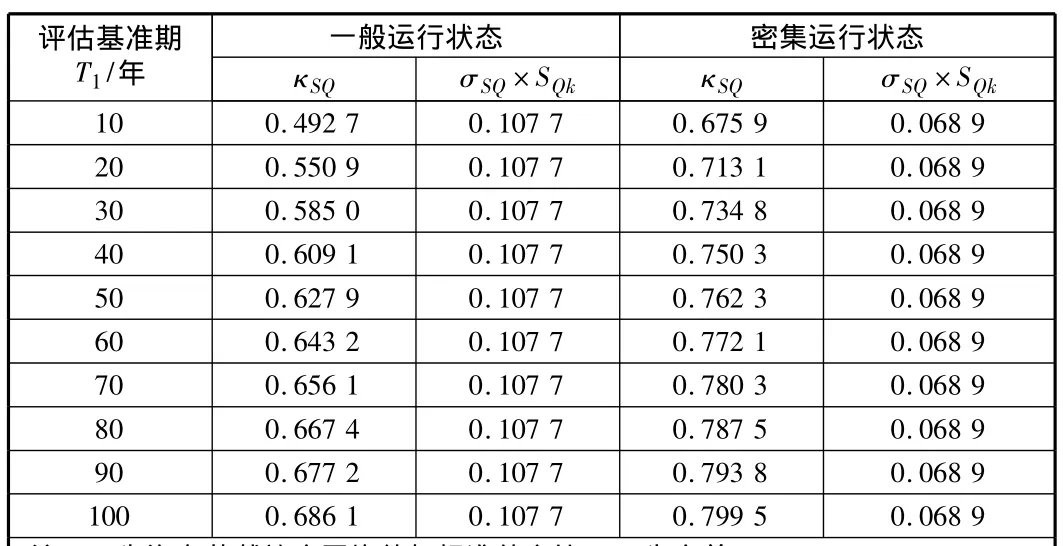
表1 不同评估基准期荷载效应最大值随机变量的统计参数

4 建立受弯构件临界寿命曲线

分析中，借鉴承载能力的分析方法［5，6］，按现行规范设计的桥梁，可不计结构安全等级的影响，相应的最低可靠指标为3.7。表2列出了以受弯构件为例，计算不同评估基准期与最低可靠指标对应的抗力分项系数。

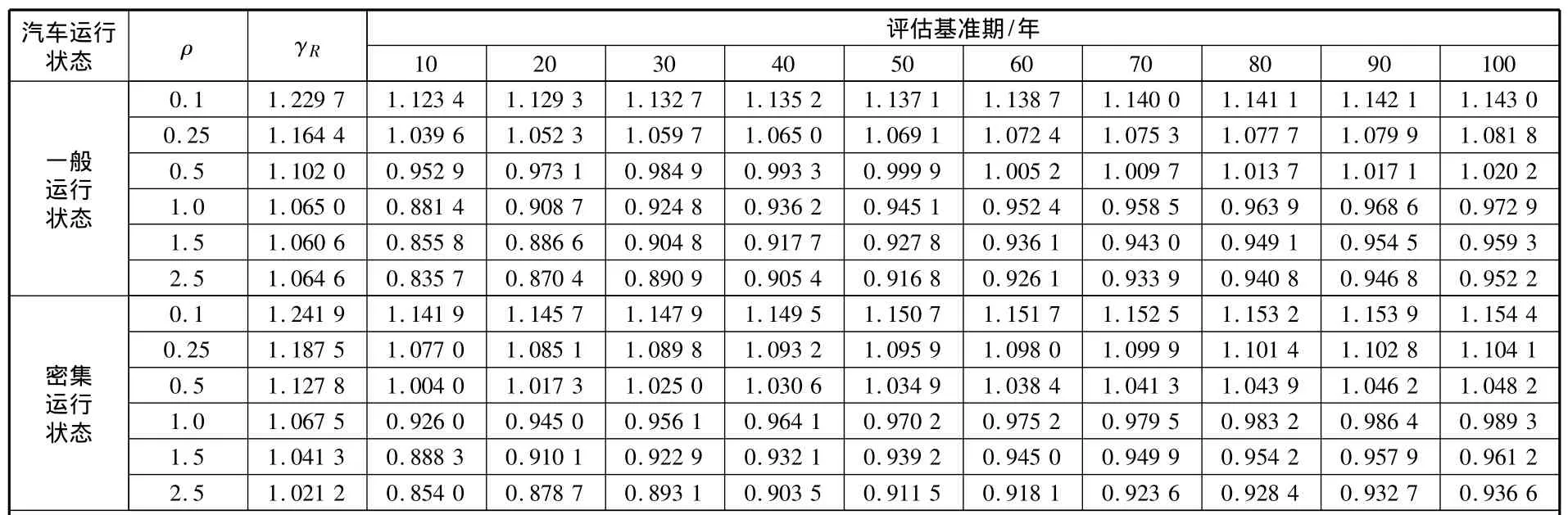
表2 不同评估基准期与最低可靠指标对应的抗力分项系数

5 结语

通过引入抗力简单随机过程模型，建立了在役桥梁构件剩余寿命预测方法，该方法避免了复杂的计算过程，大大简化了在役桥梁寿命预测工作的难度，具有很高的工程实用价值。

［1］Marchand J，Samson E.Predicting the service-life of concrete structures-Limitations of simplified models［J］.Cement and Concrete Composites，2009，31(8):515-521.

［2］Sohanghpurwala A A.NCFRP558:Manual on Service-life of Corrosion-Damaged Reinforced Concrete Bridge.

［3］Superstructure Elements［R］.Washington，D C:Transportation Research Board，2006.

［4］Markeset G.Critical chloride content and its influence on service life predictions［J］.Materials and Corrosion，2009，60(8):593-596.

［5］张 誉，蒋利学，张伟平，等.混凝土结构耐久性概论［M］.上海:上海科学技术出版社，2003:237-254.

［6］吕颖钊.在役混凝土桥梁可靠性评估与寿命预测研究［D］.西安:长安大学，2006.

［7］王松根，李松辉.基于可靠性的桥梁抗剪承载力临界寿命曲线［J］.公路交通科技，2010，27(4):84-88.

［8］王钧利.在役桥梁检测、可靠性分析与寿命预测［M］.北京:中国水利水电出版社，2006.

［9］赵尚传.钢筋混凝土结构基于可靠度的耐久性评估与试验研究［D］.大连:大连理工大学，2001.

［10］LRFR-1.Guide manual for condition evaluation and load and resistance factor rating(LRFR)of highway bridges(1st Edition and 2005 Interim)［S］.

［11］BR-MCEB-2-I2.Manual for condition evaluation of bridges(2nd Edition with 2001 and 2003 Interim Revisions)［S］.

［12］MOSES F.NCFRP Report 454:Calibration of load factors for LRFR bridge evaluation［R］.Pittsburgh:University of Pittsburgh，2001.

［13］Torres-Acosta A A，Navarro-Gutierrez S，Terán-Guillén J.Residual flexure capacity of corroded reinforced concrete beams［J］.Engineering Structures，2007，29(6):1145-1152.

［14］Duprat F.Reliability of RC beams under chloride-ingress［J］.Construction and Building Materials，2007，21(8):1605-1616.

［15］Enright M P，Frangopol DM.Service-life prediction of deteriorating concrete bridges［J］.Journal of Structural Engineering，

1998，124(3):309-317.

［16］GB/T 50283-1999，公路工程结构可靠度设计统一标准［S］.