高速电脑绣花机横梁的动态分析与优化设计
2013-08-23崔卫国周俊荣李志飞
崔卫国,周俊荣,2,李志飞
CUI Wei-guo1,ZHOU Jun-rong1,2,LI Zhi-fei1
(1.五邑大学 机电工程学院,江门 529020;2.江门展艺电脑机械有限公司,江门 529085)
0 引言
电脑绣花机是一个多机构、多激励、多响应的动态力学系统,它具有高速度、高效率的特点,但由于主轴转速不断提高时,绣花机横梁的振动会更加剧烈,断线率会更加严重,这样会大大降低刺绣产品的质量。针对以上存在的问题,本文对江门某公司生产的高速ZY-EMSD-A920型电脑绣花机的横梁进行了有限元模态分析、有限元谐响应分析,获得了前四阶固有频率和振型以及各测点随频率曲线变化,然后对其横梁进行了模拟优化改进和模型优化动态特性验证,对今后绣花机结构改进和新机型的开发提供了新的参考方向。
1 横梁有限元模型的建立
图1为高速ZY-EMSD-A920型电脑绣花机横梁简图,其长宽为300mm×200mm、壁厚为8mm矩形钢管,梁长约7000mm,上面固定有20个重量为3.9kg的机头,两端焊接在立柱支架上,立柱支架是由中立柱、前立柱和后立柱共三根组成,它们排焊接在绣花机横脚上,为了如实的得到横梁结构的实际动态性能,将工作针箱简化为质量、质心与实际完全相符的等量质量块,选择三维20节点单元,划分网格,共有112675个单元,由于横梁的两根支撑的中间伸出部分与机架焊接在一起,两根支撑由长宽为150mm×150mm、壁厚为5mm矩形钢管构成,而机架的刚度非常大,所以在两根支撑梁的中间部分施加位移为0的约束,支撑底部由一个螺栓与基础固接,为了获得与实际相符的横梁固有属性,对横梁施加接近实际情况的边界条件约束。如图1所示为绣花机横梁的有限元模型图。
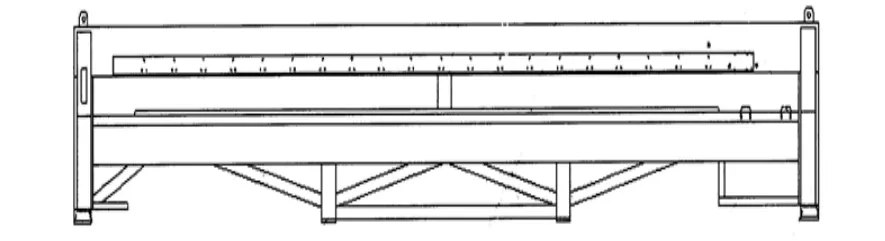
图1 绣花机横梁简图

图2 绣花机横梁的有限元模型图
2 有限元模态分析
ZY-EMSD-A920型电脑绣花机横梁为钢结构,其材料为各向同性,输入钢的各项物理参数如下:杨氏模量为200Gpa,泊松比为0.27,密度为7800kg/m3,采用Block Lanczos法对绣花机的横梁进行振动模态分析,由于低阶固有频率及相应振型对动态特性的影响最大,故只需要了解前四阶的固有频率和振型特性,经过ANSYS12.0计算,得到了图3所示的模态分析前四阶固有频率和图4所示的横梁结构前四阶振型。

图3 模态分析前四阶固有频率
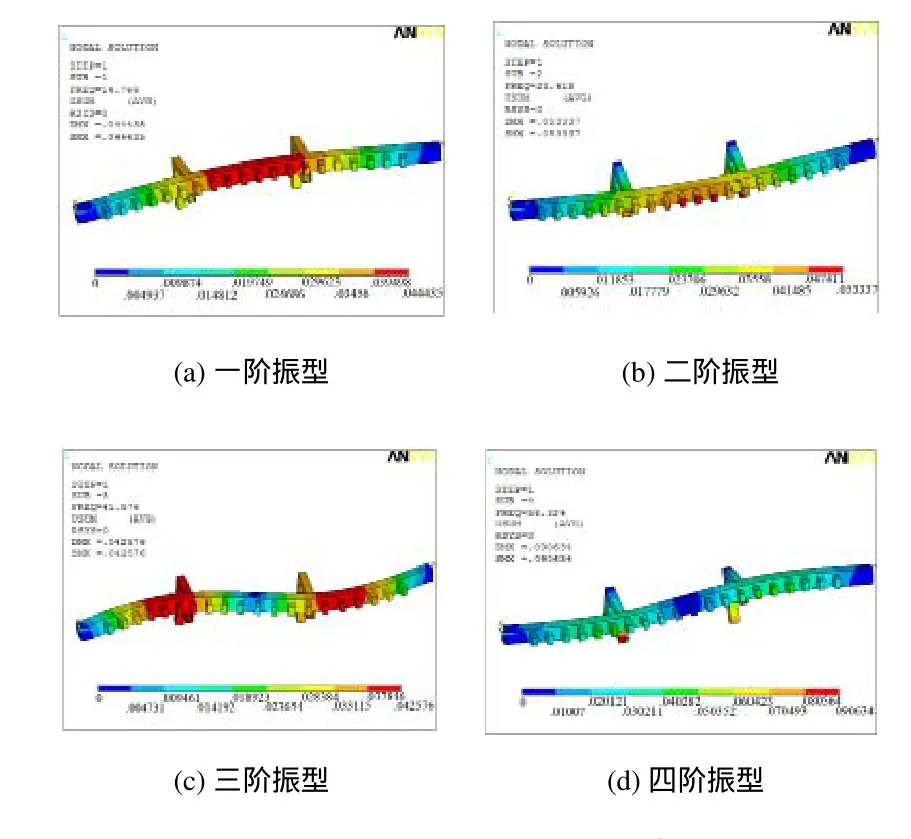
图4 横梁结构前四阶振型图
从振型图可以看出,横梁的一阶振型表现为沿水平方向中间弯曲,二阶振型为沿竖直方向中间弯曲,三阶振型为沿水平方向两端弯曲,四阶振型为沿竖直方向两端弯曲,当电机工作转速在850rpm左右时,接近横梁的一阶固有频率,此时会造成横梁中部沿水平方向的剧烈振动,从而影响刺绣精度和工作效率。
3 有限元谐响应分析
为了分析横梁在共振频率下的位移幅值响应,所以,对其进行有限元谐响应分析,分别在横梁模型的中点以及距离横梁模型左、右两端600mm处设置三个硬点,依次为左部测点1、中部测点2和右部测点3,图5所示为谐响应分析测点布置图。
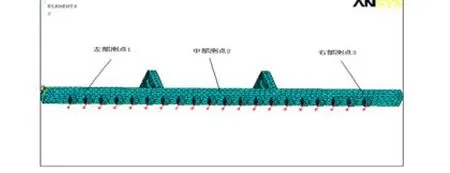
图5 谐响应分析测点布置图
电脑绣花机在高转速下性能不稳,振动剧烈,但十分具有研究价值,为此,以这三点为研究对象,提取各个测点在不同转速下的谐响应分析结果,如图6所示为各测点随频率曲线变化图。

图6 各测点随频率曲线变化图
经过有限元谐响应分析可知,在一阶、二阶固有频率处,各条曲线都表现为在横梁中部的振动位移最大,两端振动位移较小,横梁变形量从左右两端到中部呈递增状态,在中部变形量达到最大,如工作转速在850rpm时,在一阶固有频率处中部点沿水平振动位移达到2.23mm,左右两点振动位移平均在0.5mm,在二阶固有频率处中部点沿竖直方向振动位移达到2.06mm,左右两点振动位移平均在0.38mm。纵向来看,以中部测点2为例,中部测点在各转速下(从低到高)水平方向的振动位移分别为:1.13mm、1.38mm、1.58mm、1.81mm、2.01mm、2.23mm,其它测点在各方向上的振动位移规律也是如此。
4 模拟优化改进
4.1 设计变量
由电脑绣花机横梁的机构特征可知,横梁截面形状只有x1、x2、x3三个参数变量,所以设计变量集为:
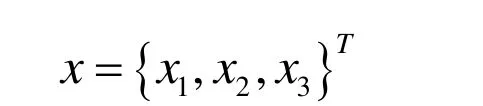
其中:x1为横梁截面的宽度;x2为横梁截面的高度;x3为横梁截面的厚度。
4.2 状态变量
在电脑绣花机横梁的优化设计中,主要是在提高其一阶固有频率的条件下,不至于过大的增加横梁的重量,因此可以将限制横梁的重量作为约束条件,即对截面尺寸加以限制,通过ANSYS12.0的分析计算,横梁结构的总重量为1014kg,对横梁重量进行约束,本文设置的重量最大值不超过1300kg,其约束不等式表示为:

其中:WT表示横梁的重量。
对设计变量进行约束,约束不等式表示为:

4.3 目标函数
在横梁的截面优化设计中,把提高绣花机横梁的一阶固有频率定义为目标函数,由于在ANSYS12.0分析软件中,是以最小化作为目标函数,如果要最大化固有频率,可以用一个足够大的数值减去一阶固有频率作为目标函数。本文中采用的目标函数为:
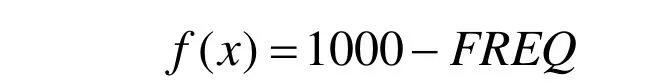
其中:FREQ表示横梁一阶固有频率。
4.4 优化结果
根据设计变量、状态变量、目标函数等参数建立优化过程中所需要的分析文件和优化数据库,应用迭代法进行优化,经过计算机迭代计算后,得出各设计变量、状态变量、目标函数的迭代过程如图7所示。
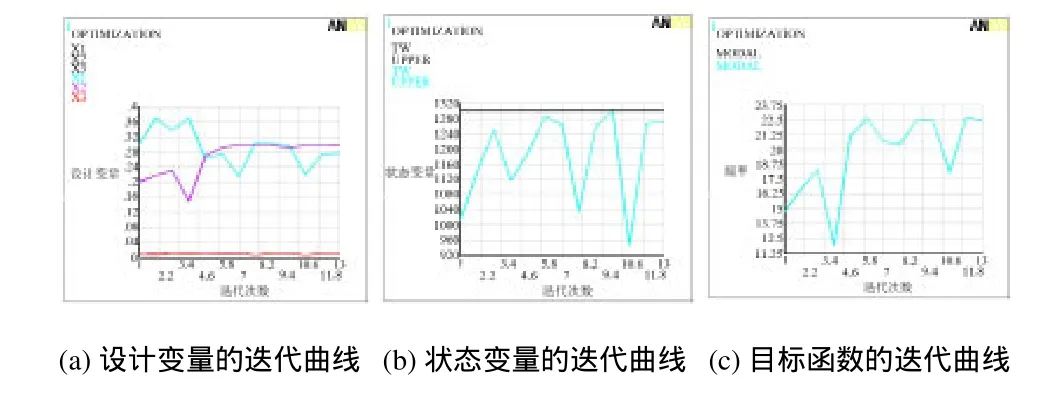
图7 迭代曲线图
对迭代曲线图进行分析,易知各项优化数据符合优化的要求,对设计变量的结果圆整取x1=0.28,x2=0.3,x3=0.012,得到取整后横梁重量为1271.3kg,比优化前重量1014kg增加了257.3kg,一阶固有频率由原来的14.8Hz增加到22.7Hz,优化效率达53.4%,优化效果明显。
5 模型优化动态特性验证
对优化取整后的横梁进行模态分析,将所得前四阶固有频率和优化前进行对比,如表1所示。

表1 优化后的固有频率值
对其进行谐响应分析,所有参数设置和提取结果的测点设置与优化前均相同,当工作转速在850rpm高速运转的情况下,其结果如图8所示。

图8 优化后测点变形VS频率图
由图可以看出,优化后横梁在一阶固有频率处的振动位移为0.65mm,比优化前的振动位移2.23mm明显减小,而且优化后横梁在第三、四阶固有频率处的振动位移基本可以忽略,说明优化后的横梁高阶固有频率对横梁的动态特性影响甚小,达到了此次优化的目的。
6 结束语
结构动态分析与优化设计为高速电脑绣花机横梁的设计提供了一种可靠高效的设计方法,提高了电脑绣花机的研制与开发的效率。降低了高速电脑绣花机横梁振动引起的断线率问题,提高了刺绣产品的质量。采用的模拟优化改进方法,具有速度快、可靠性好的特点,可应用在相关机型的快速优化改进研发上。
[1]周俊荣,郑为东.电脑绣花机刺布机构与挑线机构运动分析[J].上海工程技术学院学报,2008,6,22(2):136-128.
[2]李志飞.高速电脑绣花机横梁的动态特性分析与结构改进[D].江门:五邑大学,2013.
[3]白皛,赵罘,林建龙,辛洪兵,龚堰珏.绣花机横梁的模态分析及优化设计[J].机械设计与研究,2010,02,26(1):111-112.
[4]林建龙,王小北,赵丽萍.电脑绣花机的横梁减振实验探讨[J].纺织学报,2007,12,28(12):121-123.
[5]潘丹丹.某电脑绣花机动力学仿真分析与减振研究[D].南京:南京理工大学,2012.
[6]陈兆廷,陈鹏.一种减振降噪电脑绣花机机架:中国,00111049.7[P].2001-05-19.
[7]曹建华.双铣头数控螺杆铣床的有限元分析及优化设计[D].江门:五邑大学,2010.
[8]蔡共宣,林富生.工程测试与信号处理[M].武汉:华中科技大学出版社,2006.
[9]刘刚,零点工作室.Labview 8.20中文版编程及应用[M].北京:电子工业出版社,2008.
[10]陈展新.多头绣花机机架:中国,200420044850.3[P].2005-07-06.
[11]林建龙,傅成,梦春玲,门桂香.电脑刺绣机针杆机构力平衡设计[J].机械设计与制造,2004(6):23-24.
[12]蒋春松,孙浩,朱一林.ANSYS有限元分析与工程应用[M].北京:电子工业出版社,2012.
[13]赵延雯,吴世林,方晓初.富怡牌电脑绣花机工作原理[J].武汉科技学院学报,2000(2):89-94.
[14]高华斌.电脑绣花机:新增长点更需精确度稳定性[J].中国纺织报,2010.
[15]季文美,方同.机械振动[M].北京:科学出版社,1985.
[16]汪凤泉,郑万泔.试验振动分析[M].江苏:江苏科学出版社,1987.
[17]Guan, D.H.,Yam,L.H.,Mignolet, M.P., Li, Y.Y.Experimental modal analysis of tires,Experimental Techniques,2000,6(24):39-45.
[18]涂振飞.ANSYS有限元分析工程应用实例教程[M].北京:中国建筑工业出版社,2010.8.
