γ－Reθ模式应用于高速边界层转捩的研究

孔维萱，阎 超，赵 瑞

（北京航空航天大学 航空科学与工程学院，北京 100191）

0 引 言

在高超声速飞行条件下，边界层转捩直接关系到飞行器摩擦阻力、热交换及流动的分离位置等，若能准确预测转捩位置或延迟转捩的发生，可有效改进飞行器气动性能，大大降低燃料消耗，使热防护设计更为灵活。另一方面发动机唇口流动品质是发动机工作的重要参数之一，流动为湍流态时燃气成分掺混充分，保证燃烧效率；正确控制流动状态，强制流动发生转捩已成为高超声速一体化飞行器设计的重点难题。研究边界层转捩及其预测方法，对于飞行器气动设计和进气道一体化设计具有重要的工程意义。

风洞实验一直是研究流动转捩的重要手段，近年来静风洞的研究成果［1－3］成为模拟真实飞行状态流动转捩和验证数值方法的重要依据。随着计算流体力学的发展，数值试验已逐渐成为与风洞实验同等重要的流体力学研究方法。其中基于模式理论发展的转捩模式，以其稳定性和经济性成为最具有工程应用前景的转捩模拟和预测方法。Mayle等［4］提出非湍流脉动能概念，模化转捩前的流动脉动，随后 Warren等［5］将其耦合在湍流模式中，形成了一方程的转捩模式。Menter等［6］提出了一种避免求解积分量的基于当地变量的转捩模式，此模式在众多亚声速转捩流动中表现优秀；值得一提的是该模式特别针对分离导致的转捩对间歇因子提出了修正，并在部分算例中得到良好的效果。符松和王亮［7］提出了适用于超声速流动的转捩模式，该模式统一求解非湍流脉动和湍动能，并以脉动与平均流动的关系作为转捩起始的判据，考虑多种不稳定扰动模态对了流动的影响。

本文采用γ－Reθ模式对超声速、高超声速流动的典型模型进行计算，研究了来流马赫数、来流雷诺数、攻角状态和头部钝化半径对流动转捩的影响，就γ－Reθ模式针对上述流动参数变化的适用性进行讨论。

1 计算方法

1．1 控制方程

计算采用有限体积法求解可压缩全N－S方程，无粘通量由Roe的FDS格式求解，粘性通量采用中心差分格式进行离散，时间推进采用LU－SGS隐式方法。

1．2 转捩模式

本文采用γ－Reθ模式模拟流动的转捩。γ－Reθ模式是Menter及合作者［6］提出的转捩模式，引入涡雷诺数概念将边界层相关量的求解当地化，建立输运方程求解间歇因子和临界动量厚度雷诺数，在SST湍流模式的基础上实现了对于流动转捩的计算模拟和预测。

1．2．1 当地雷诺数输运方程

转捩起始位置的求解对于转捩计算和预测至关重要，γ－Reθ模式中求解“临界动量厚度雷诺数~Reθt”输运方程从而给出转捩起始位置的相关信息，与由经验公式或转捩判据确定转捩起始位置的方法相比，此方法能够更多地反映当地流动特性。当地雷诺数输运方程表示为：

其中生成项为：

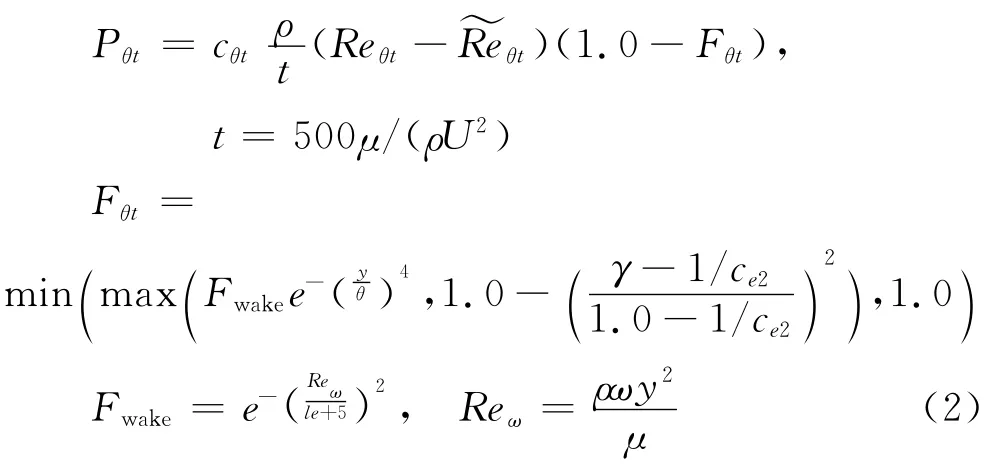
转捩动量厚度雷诺数Reθt由来流湍流度和压力梯度等参数拟合的经验公式，表示为：

模式常数为：

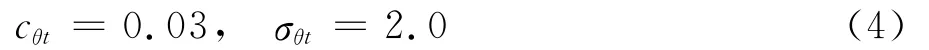
1．2．2 间歇因子输运方程

将间歇因子作为权值耦合层流与湍流区域的计算，采用输运方程求解间歇因子，间歇因子输运方程为：

间歇因子的生成项和耗散项分别表示为：

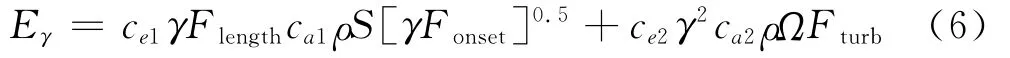
决定间歇因子增长的关键参数是Fonset，由下式确定：

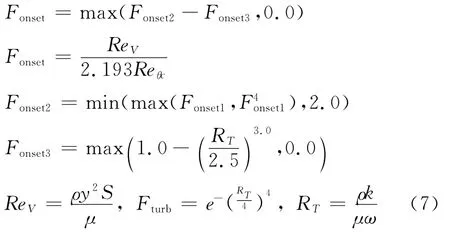
其中Reθc表示间歇因子开始增长处的动量厚度雷诺数，可表示为的函数：

确定间歇因子生成项的另一关键参数为Flength，表示转捩区的长度，同样以的函数形式给出如下：

其它模式常数为：

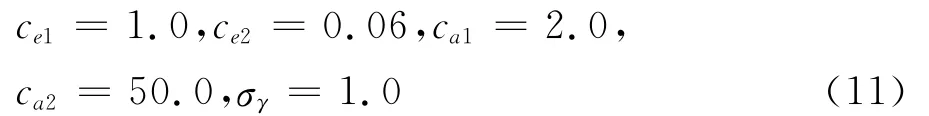
γ壁面法向通量为0；为抑制入口处湍动能的耗散现象，γ设置为1。

1．2．3 模式最终形式

间歇因子体现在原SST模式中湍动能生成项和耗散项中，γ－Reθ转捩模式的最终形式如下：

2 数值实验

2．1 数值格式对转捩模式的影响

数值格式本身的特性是影响数值模式的关键因素之一，这里选取超声速平板流动算例，采用二阶格式包括Roe的FDS格式（分别组合min－mod和superbee限制器）、AUSM＋格式和五阶 WENO格式进行计算，研究不同格式对转捩模拟的影响。超声速平板流动条件为：来流马赫数4．5，来流雷诺数6．433×106／m，来流温度61．1K，来流湍流度0．1%。计算域设置为1m×0．33m，保证法向第一层网格y＋＜1。入口给定速度、压力、k和ω。

图1给出壁面摩阻系数沿流向分布情况，比较各种格式计算结果可知：同为二阶格式时，限制器的选择对计算结果的影响明显，其中压缩性较强的superbee限制器计算得到的转捩位置明显提前于耗散性较大的min－mod限制器结果；不同格式计算结果差异不大；相对于二阶格式，高阶格式对流动结构的刻画更为精确，数值耗散小，但计算稳定性差，并对存储量和计算量提出了更高的要求。对于使用γ－Reθ模式的转捩预测，计算格式的影响主要体现在格式的耗散性上，耗散较小的计算格式得到的转捩位置较耗散性大的格式提前，是由于γ－Reθ转捩模式中控制间歇因子γ生成的函数Fonset与粘性负相关，即体现为数值粘性越小转捩发生位置越提前。在原有模式参数设置的基础上，耗散性较大的格式计算结果与DNS数据吻合较好，综合考虑计算稳定性等因素，下文各算例均采用Roe格式组合min－mod限制器的空间离散方法进行计算。

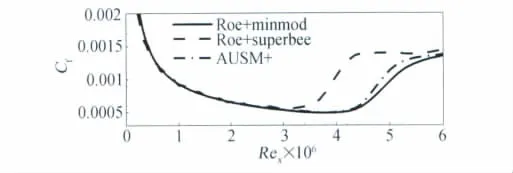
图1 马赫4．5平板壁面摩阻系数分布Fig．1 Skin－friction coefficient distribution for M4．5plate

2．2 算例描述

应用γ－Reθ模式计算以下算例：（1）马赫3．5、半锥角为5°尖锥；（2）马赫5．91、半锥角5°尖锥；（3）马赫5．91、半锥角5°裙锥和（4）马赫7．16、半锥角7°尖锥。其中马赫3．5尖锥计算了6种雷诺数条件，讨论来流雷诺数对流动转捩的影响。针对马赫5．91尖锥和裙锥的计算，讨论不同攻角状态对转捩的影响。7°半锥角尖锥算例中给出了三种头部钝化半径的计算结果，讨论头部钝化半径对流动转捩的影响。

各算例流动参数和计算设置列于表1，需要说明的是，针对各算例分别设置湍动能及比耗散率的入口条件，以尽量保证计算来流湍流度与实验或参考文献相同。

表1 各算例流动参数及网格设置Table 1 Flow condition and grid refinement

以下给出各算例计算结果和讨论。

2．3 雷诺数对转捩的影响

计算长为550mm、半锥角为5°的尖锥，讨论不同来流雷诺数条件下流动转捩情况。流动条件参照实验［8］设置，来流马赫数为3．5，来流湍流度为0．1%，来流雷诺数分别为：2．69×107、3．70×107、4．69×107、5．66×107、6．59×107和7．49×107。计算网格设置（流向×法向×周向，下同）为121×121×81，法向第一层网格高度为1．0E－6m；流动入口给定速度、温度、压力、k和ω，壁面提无滑移、绝热条件，出口提远场条件。

图2 马赫3．5尖锥计算结果Fig．2 Skin－friction coefficient distribution for M3．5cone

图3 马赫3．5尖锥计算结果Fig．3 ReTvs．Re／m from M3．5cone results

图2 给出马赫3．5圆锥计算结果，图中实线（由左侧坐标标示）表示壁面摩阻系数，离散点（由右侧坐标标示）表示壁面恢复温度风洞实验值，恢复温度定义为r＝（Taw－Te）／（T0－Te）。随来流雷诺数的增大，γ－Reθ模式计算结果呈现出：转捩起始位置逐渐向上游移动、转捩后摩阻系数的峰值逐渐增大的变化趋势。在较小的来流雷诺数条件下，模式计算的转捩起始位置明显比实验提前，随着来流雷诺数的增大，这一差异逐渐减小。

图3比较了飞行实验、风洞实验和γ－Reθ模式计算的转捩雷诺数随来流雷诺数的变化趋势。γ－Reθ模式计算结果与飞行实验变化趋势相同，可以证实γ－Reθ模式能够正确反映流动转捩随来流雷诺数的变化；但模式计算的转捩雷诺数整体小于飞行实验结果，说明γ－Reθ模式未考虑可压缩性对流动的稳定作用，在超声速流动（Ma～3．5左右）条件下预测的转捩位置提前，转捩雷诺数较小。而风洞实验结果只在来流雷诺数较小时与飞行实验结果吻合良好，而随着来流雷诺数的增大，风洞自身的噪声很大程度上影响了流动转捩的结果。

2．4 攻角对转捩的影响

计算裙锥和圆锥0°～4°攻角流动，讨论小攻角对流动转捩的影响。圆锥长635mm、半锥角为5°；裙锥前半部为长254mm、半锥角为5°尖锥，后半部为曲率半径2364mm的尾裙，特别设计的曲率半径使流动在尾裙区域具有逆压梯度，并保持边界层厚度不变。头部钝化半径均为0．8mm，裙锥模型几何外形如图4所示。

图4 尖锥裙几何外形示意图Fig．4 Geometry for flared－cone

流动参数参照风洞实验［9－10］设置，来流马赫数为5．91，来流雷诺数为 9．348E6／m，来流湍流度为0．1%，来流温度为56．2K。网格设置为121×121×41，法向第一层网格高度1．0E－6m；边界条件设置与上一算例相同。

图5为马赫5．91尖锥裙流动计算结果。图5（a）给出0°攻角时对称面压力等值线分布，除尖锥前缘产生的斜激波外，尾裙区域存在一簇较弱的压缩波。图5（b）给出0°攻角母线、2°攻角迎风、背风子午线压力系数分布。γ－Reθ模式计算的压力系数与实验值吻合良好，最大差异在裙锥尾部；图5（b）中可以看到，实验结果2°攻角背风面尾裙中部位置出现压力系数的局部下降，这一流动未能由γ－Reθ模式计算再现。实验测得0°攻角转捩发生在x＝371mm位置，2°攻角背风侧转捩位置提前至x＝310mm，迎风侧基本保持层流状态不发生转捩。计算结果与实验相同，图5（c）给出0°和2°攻角壁面法向第一层网格间歇因子分布，0°攻角间歇因子在x＝370mm开始增长；2°攻角时背风子午线间歇因子开始增长位置提前至x＝300mm，迎风子午线间歇因子保持在很小数值。

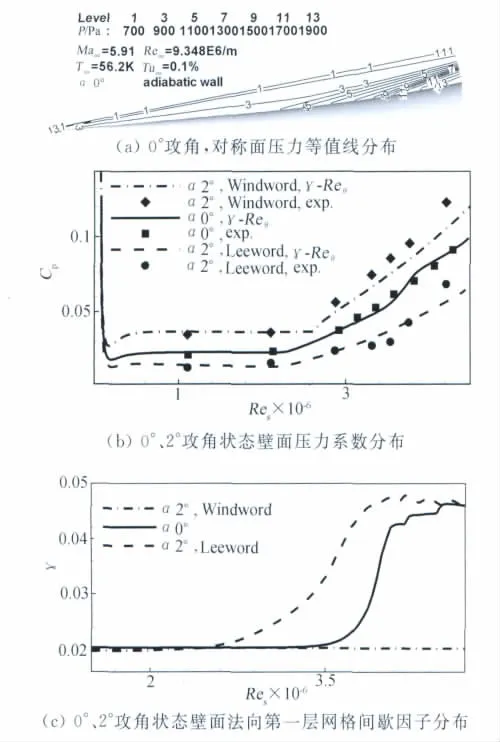
图5 M5．91裙锥流动计算结果Fig．5 Results for M5．91flared－cone

图6 给出马赫5．91直圆锥计算结果。图6（a）为0°攻角壁面热流系数与实验对比，计算结果与实验值基本吻合，但转捩起始位置较为提前。图6（b）给出1°、2°和4°攻角壁面法向第一层网格间歇因子分布。同裙锥计算结果相似，当攻角由0°变为1°时，背风侧转捩位置明显提前，迎风侧转捩位置推后；随着攻角的增加，迎、背风侧转捩位置逐渐向下游移动，且周向转捩线倾斜程度逐渐增大。

分析本节两算例的计算结果，γ－Reθ模式通过求解当地雷诺数输运方程得到转捩起始位置的相关信息，并结合当地雷诺数确定间歇因子，计算能够一定程度上反应边界层的三维特性，在未引入横向不稳定扰动模化的情况下，能够正确预测小攻角对流动转捩的影响。

图6 马赫5．91直圆锥计算结果Fig．6 Results for M5．91cone

2．5 头部钝化对转捩的影响

最后讨论头部钝化半径对流动转捩的影响，选取长2300mm、半锥角为7°的圆锥进行研究，头部钝化半径（Rn／mm）分别取为2．5、5．0和6．35，以头部钝化半径为特征长度的雷诺数（ReRn×10－4）分别为2．55、5．1和6．477。流动条件参照实验［11］给定，来流马赫数为7．16，来流湍流度为0．675%，来流温度为231．7K，壁面提绝热条件。计算网格设置为121×121×41，法向第一层网格高度为1．0E－6m；边界条件设置与上一算例相同。

图7为马赫7．16圆锥流动计算结果，图7（a）和（b）给出头部钝化半径分别为2．5mm和5．0mm时壁面热流值与实验对比，热流峰值的位置和大小等计算结果与实验值基本相同，但同样存在预测转捩起始位置较早的问题。头部钝化半径的变化对于转捩的影响，主要源于压力梯度的变化；由于球头与锥体相接处存在曲率半径的突变，在该位置产生较大逆压梯度，从而影响流动转捩的发生。图7（c）给出圆锥前缘局部压力分布及壁面压力梯度（∂p／∂s）分布，可见随着头部钝化半径的增加，逆亚梯度峰值位置逐渐向下游移动；压力梯度的变化对流动转捩的影响表现为，随着头部钝化半径的增加，转捩位置向下游移动，转捩后的热流峰值有一定程度的降低。模式能够正确模拟头部半径对流动转捩的影响，针对压力梯度进行了修正提高了对于此类问题的适用性。

图7 马赫7．16尖锥计算结果Fig．7 Results for M7．16cone

3 结 论

（1）将γ－Reθ模式应用于超声速、高超声速边界层转捩问题的计算，讨论了来流雷诺数、攻角状态和头部钝化半径等关键参数变化时的模式性能。数值实验表明γ－Reθ模式具有一定的预测超声速、高超声速转捩的能力。

（2）马赫数3至7范围内的圆锥类流动中，γ－Reθ模式对转捩位置的预测普遍提前，来流雷诺数较小时尤为明显。随头部钝化半径的增大，γ－Reθ模式计算得到的转捩起始位置后移，对于压力梯度的变化敏感。

（3）γ－Reθ模式未针对横流不稳定性进行特别模化，但能够正确模拟马赫6圆锥或裙锥小攻角状态下的边界层转捩。相比于0°攻角，小攻角时背风侧转捩位置提前、迎风侧转捩延迟；随攻角的增加，周向转捩线变陡峭并向下游移动。

［1］ SCHNEIDER S．A Review of hypersonic boundary layer stability experiments in a quiet Mach 6wind tunnel［R］．AIAA 1997－1819，1997．

［2］ LACHOWICZ J，CHOKANI N，et al．Boundary－layer stability measurements in a hypersonic quiet tunnel［J］．AIAA J．，34（12）：2496－2500，1996．

［3］ CHEN F，MALIK M，et al．Boundary－layer transition on a cone and flat plat at Mach 3．5［J］．AIAA J．，27（6）：687－693，1989．

［4］ MAYLE R，SCHULZ A．The path to predicting bypass transition［J］．J．Turbomach，1997，119：405－411．

［5］ WARREN E，HARRIS J，HASSAN H．Transition model for high－speed flow［J］．AIAA J．，1995，33（8）：1391－1397．

［6］ LANGTRY R，MENTER F．Correlation－based transition modeling for unstructured parallelized computational fluid dy－namics codes［J］．AIAA J．，2009，47（12）：2894－2906．

［7］ 王亮，符松．一种适用于超音速边界层的湍流转捩模式［J］．力学学报，2009，41（2）：162－168．

［8］ CHEN F，MALIK M，et al．Boundary－layer transition on a cone and flat plat at Mach 3．5［J］．AIAA J，1989，27（6）：687－693．

［9］ DOGGETT G，CHOKANI N，WILKINSON S．Effects of angle of attack on hypersonic boundary layer stability in a quiet wind tunnel［J］．AIAA J，1997，35（3）：464－470．

［10］HORVATH T，BERRY S，et al．Boundary layer transition on slender cones in conventional and low disturbance Mach 6wind tunnels［R］．AIAA 2002－2742．

［11］JOHNSON H，ALBA C，et al．Boundary layer stability analysis to support the HiFiRE transition experiment［R］．AIAA 2007－0311．