基于SST湍流模型的二维操纵面空化流场研究

邬 明，孙善春

（中国船舶重工集团公司第七一○研究所，湖北 宜昌 443003）

0 引 言

超空泡技术是一种可以使水下航行体高效减阻技术，其原理是在水与航行体表面形成稳定的气层，达到减小水的粘性阻力，从而提高水下航行体的运行速度。水下超空泡航行体所采用的操纵面，要兼顾全沾湿状态和超空泡状态时的流体动力布局要求：航行体处于全沾湿状态时，航行器流体动力布局与常规水下航行体相似，需依靠操纵面提供稳定力矩和操纵力矩。而在超空泡状态时要尽量减小其所受阻力，同时操纵面必须穿透空泡壁进入水中才能提供所需力矩，该状态下的操纵面应具有较高的升阻比，因此对于操纵面的研究具有重要意义。

随着计算性能的快速提高和计算数学理论的不断发展完善，数值方法已经成为研究问题和解决问题的重要手段之一，它不仅在理论研究领域得到普遍应用，而且在工程实际中也被广泛使用。求解雷诺平均N－S方程式是当前数值计算的主要方法，需补充湍流模型对方程进行封闭。湍流模型对于数值模拟空化流场的精度具有决定性影响。当前应用最普遍的湍流模型是k－ε 湍流模型［1－2］，然而该模型有以下不足之处：在模型中湍流尺度未知；仅限于湍流边界层压力相对稳定的情况；其壁面函数在边界层的修正中难以弥补计算模型与实际现象之间的差距。相对于k－ε湍流模型的以上不足之处，SSTk－ω湍流模型［3］却拥有以下优点：该模型能够适应逆压梯度变化的各种物理现象；可应用于粘性内层，通过对壁面函数的应用，能够精确模拟边界层的现象，无需使用较容易失真的粘性衰减函数。本文将SSTk－ω湍流模型应用于操纵面空化流场的仿真分析中，取得了较好的结果。

SSTk－ω湍流模型以下简称SST湍流模型。

1 控制方程与算法

1．1 连续方程

式中：ρ表示密度；U表示速度；t为时间。

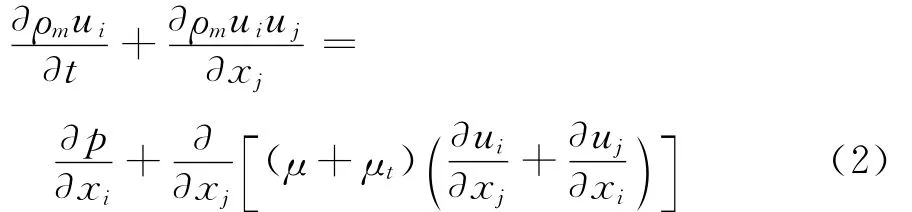
其中

μt和αl分别表示流体动力粘度和水相的体积分数。

1．2 湍流模型

若分别以φ1、φ2、φ3表示k－ω 模型、k－ε 模型和SST湍流模型中的函数关系，则SST湍流模型可表示为：

SST湍流模型考虑到湍流剪切应力的输运，不但能够对各种来流进行准确的预测，还能在各种压力梯度下精确模拟分离现象，其综合了近壁面k－ω模型的稳定性及边界层外部k－ε模型独立性的优点，它的计算模拟性能优于后两者。各系数取值为β′＝0．09，α1＝5／9，β1＝0．075，σk1＝2，σω1＝2，α2＝0．44，β2＝0．0828，σk2＝1，ωω2＝1．168，各个数据的取值取自参考文献［4］。

2 空化模型

选择Singhal空化模型［5］，其中 Rayleigh Plesset方程是控制汽化产生和空泡凝结的理论基础，该方程描述了液体中空泡的变化过程：

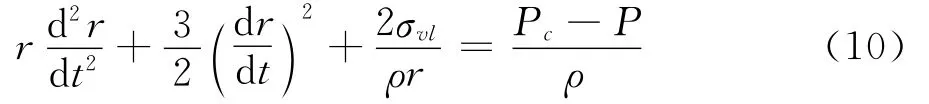
式中r为空泡半径，Pc为汽化压强，σvl是汽液两相间的表面张力系数，质量传输率为：

式中，ρg表示饱和蒸汽密度；sgn表示符号函数；NB代表单位体积的汽泡数；F代表经验因子，汽化过程和凝结过程取值不同，Fvap＝50，Fcond＝0．01。

3 计算模型

3．1 计算区域和网格划分

针对水下高速航行体在不同运动阶段的流体动力特性，对构成操纵面的二维基本翼型进行了相应研究——选用典型的小顶角楔形，经验表明以上区域边界对流场的计算结果影响很小。

计算网格的好坏直接影响到数值计算的可行性、收敛性以及计算精度。前处理软件ICEM CFD是一款成熟的网格划分软件，它向用户提供业界领先的高质量网格技术，其强大的网格划分功能可以满足CFD仿真计算的严格要求。

对于本文中的问题若采用非结构网格，生成的空泡边界会出现凹凸不平的毛刺，影响对仿真结果的分析。若想消除毛刺现象，就要对网格进行细分。因此采用基于六面体结构化网格划分方法，对计算区域进行全六面体结构网格划分，并利用与湍流强度相关的Yplus对所建模型进行考核。楔形操纵面流场网格图及局部放大图如图1和图2所示。

图1 计算区域与网格划分Fig．1 The computational domain and meshing

图2 操纵面局部放大图Fig．2 Zooming in images locally in control surface

3．2 边界条件设定

边界条件设定：上游边界给定来流速度和各流体体积分数；下游边界给定压强；流域外边界为光滑物面边界。初始条件：设定初始来流速度和各流体体积分数。

3．3 数值方法

采用有限元的有限体积法（FVM），N－S方程中的对流项采用CFX高精度格式，它利用调整混合因子提高计算精度且平均收敛精度。以一阶迎风为例，对流项：

式中：φi表示变量φ第i个节点值；φu为变量φ迎风节点值；ξ为混合因子；▽φ为迎风节点的节点梯度；从迎风节点到第i个节点的矢量。

针对不同条件下，ξ会作出相应的调整来满足计算要求获得精确的解，例如在第i节点临近迎风节点的节点梯度变化剧烈，则混合因子趋近于0，反之趋近于1。

4 楔形操纵面的典型空泡

根据相关实验文献［6］，楔形操纵面的典型空泡形态分为三种，如图3。

图3 楔形操纵面的典型空化形态（全空化、部分空化和底部空化）Fig．3 Typical characteristics of cavities of control surface（entirely、substantially and bottom enveloped by cavities）

从图3中不难发现，当来流攻角小于楔形半顶角时，仅在翼型底部产生空化现象，而在上下翼面完全处于全沾湿状态。此时所产生流体动力和力矩与攻角近似成线性关系，且较为稳定。当来流攻角大于楔形半顶角时，上翼面处于超空泡状态，而下翼面为全沾湿状态，此时，同样可产生稳定的流体动力和力矩，且与攻角成线性关系。当来流攻角与楔形半顶角相当时，除在翼型底部产生空化外，上翼面还将出现间歇性片状空泡，此时翼型所产生的流体动力及力矩呈非定常脉动分布。

5 仿真计算结果及分析

空化数是衡量流体空化程度的物理量，计算公式为：

其中P∞、PV、ρ、V∞分别为某基准位置上的绝对静压力、空泡内的绝对静压力、流体密度、相对于物体的未扰动流体的速度。研究中设定初始条件P∞、25℃时水的饱和蒸汽压、V∞和ρ。

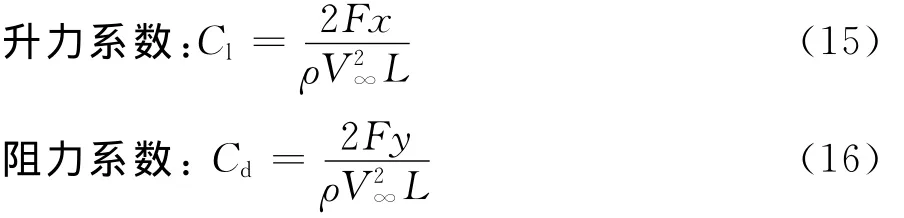
L为翼型弦长，升、阻力系数基于速度坐标系。

表1给出了绕楔形操纵面的超空化仿真与试验结果的对比。

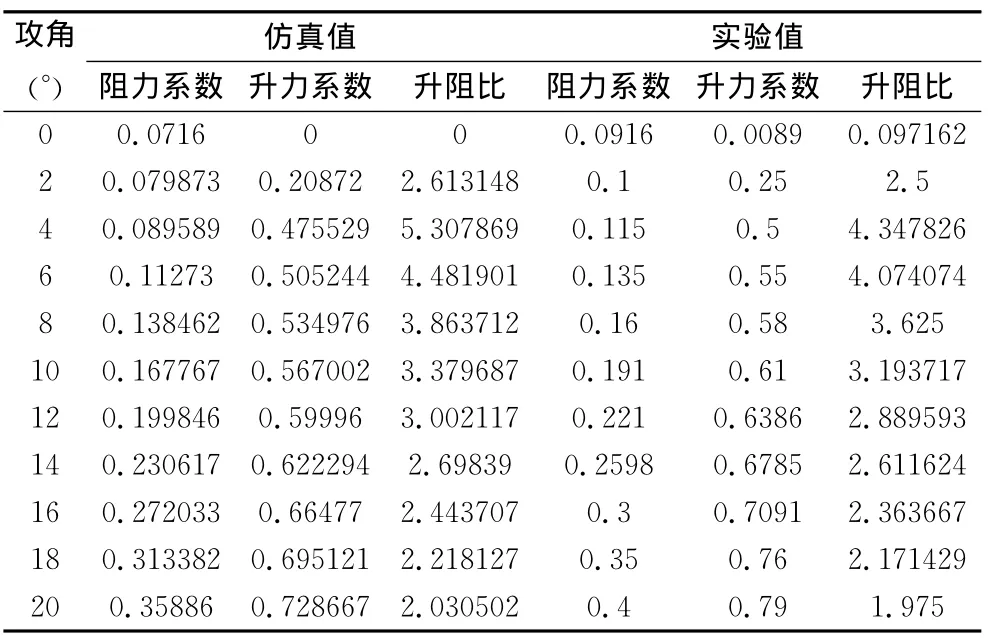
表1 绕楔形操纵面的超空化仿真与试验结果Table 1 Results of simulation and test of control surface

图4给出了计算得到的阻力系数和升力系数随攻角的变化仿真曲线及实验曲线，两者基本一致，从中可以看出当保持自然空泡数不变，仅改变来流攻角时，操纵面的阻力系数呈逐渐增大趋势，而升力系数在攻角增至一定数值后，其增大幅度减缓。随着攻角的增大，空泡不断增大，并形成超空泡，使得操纵面全部处于空泡的包裹之中，此时，操纵面的控制效率也将相应地降低。图5中的升阻比曲线分布表明，当攻角增至一定数值后，升阻比将有所减小，这与临界攻角和局部空泡的形成有关。

图4 阻力系数和升力系数随攻角的变化曲线Fig．4 The change of drag characteristics and lift characteristics by angles of attack

图5 升阻比随攻角的变化曲线Fig．5 The change of ratio of lift over drag by angles of attack

CFX后处理可以更加直观地观察空泡形态，如图6所示，不同攻角下，操纵面的密度云图。从图中可以看出，当来流攻角很小时（α＜3°），楔形操纵面底部产生空泡；当攻角较小时（3°≤α≤3．5°），在操纵面上端面产生局部空泡；而在攻角继续增大时（α≥3．5°），操纵面完全被空泡包裹，并且呈增大趋势。这与理论结果可较好地吻合。

图6 不同攻角下的密度分布图Fig．6 The contour of the charge density in different angles of attack

图7 给出的是空化数为0．323时，操纵面的压力系数分布，可看出，其下翼面上压力系数分布呈单调递减趋势，当攻角a＝3°时，上翼面出现局部空泡的压力系数分布形态，增大来流攻角后，上翼面的压力系数将降至一恒定值，即上翼面已处于超空化状态。

图7 不同攻角，操纵面表面的压力分布曲线Fig．7 The curve of pressure distribution for control surface in different angles of attack

图8 给出了不同空化数下的空泡轮廓图。从图中可以发现随着空化数的降低空泡尾部的回射流强度在减弱，这是因为空泡长细比增大，闭合时空泡边界入射角减小的缘故。这和文献［7］中的理论分析取得了很好地一致性。

图8 不同空化数下的空泡轮廓Fig．8 The profile of cavities in different citation numbers

6 结 论

采用SST湍流模型，文章对典型二维操纵面在不同来流空化数及攻角条件下的升阻力特性、空泡形态、表面压力分布规律进行了详细的研究，并与相关实验做了分析比较，结果表明：

（1）减小空化数后，相同攻角条件下的操纵面的阻力系数和升力系数都有所下降。随着攻角的增大，由于上翼面处于超空化状态，其升阻比曲线将有所减小；

（2）运用N－S方程及SST湍流模型对均质流场求解，并利用Rayleigh－Plesset空泡模型对二维操纵面的空化流动进行数值模拟，与相关实验相对比，取得了较好的一致性，证明了所选湍流模型的可行性，为以后的超空泡实验研究提供参考依据；

（3）SST湍流模型能够对操纵面的空化流场进行较为准确的模拟，尤其在空泡流场、空泡外形以及尾部回射流方面，可以准确地预测空化流场，从而指导超空泡航行器的外形设计，显示出了优越性，具有广阔的应用前景。

［1］ KUNZ R，BOGER D，STINEBRING D，et al．A preconditioned implicit method for two－phase flows with application to cavitation prediction［J］．Comput．Fluids，2000，29（8）：849－875．

［2］ LEROUX J B，COUTIER－DELGOSHA O，ASTO－LFI J A．A joint experiment and numerical study of mechanisms associated to instability of partial cavitationon two－dimensionalhydrofoil［J］．Phys．Fluids，2005，17（5）：052－101．

［3］ COUTIER－DELGOSHA O．Numerical prediction of cavitation flow on a two－dimensional symmetrical hydrofoil and comparison to experiments［J］．Journal of Fluids Engineering，2007，129（3）：279－291．

［4］ KUBOTA A，KATO H．A new modeling of cavitating flows：a numerical study of unsteady cavitation on a hydrofoil section［J］．FluidMech．，1992，240（1）：59－96．

［5］ SINGHAL A K，ATHAVALE M M，et al．Mathematical basis and validation of the full cavitation model［J］．ASME Journal of Fluids Engineering，2002，124：617－624．

［6］ GARABEDIAN P R．Calculation of axially symmetric cavities and jets［J］．Pac．J．Math．，1956，6（4）：611－684．

［7］ SEMENENKOV N．Artificial supercavitation．physics and calculation［A］．RTO AVT lecture series on supercavitating flows［C］．Von Karman Institute Brussels，Belgium：2001，206237．

［8］ 张宇文．空化理论与应用［M］．西安：西北工业大学出版社，2007．