分裂叶尖概念型风力机叶片的气动设计与数值优化研究

张震宇，王同光，陈 立，许波峰，王 珑，罗 源

（1．南京航空航天大学 江苏省风力机设计高技术研究重点实验室，江苏 南京 210016；2．中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000）

0 引 言

水平轴风力机的风能输出受到来流风况的强烈影响，在偏航以及中等、大风速条件下由于叶片背风面的边界层容易发生流动分离，并会导致扭矩输出和能量利用效率的明显降低，以及分离噪声等一系列影响。风力机叶片的上述特性通过风洞实验和计算流体力学数值模拟不断被证实［1－2］。

另一方面，水平轴风力机的大展弦比布局一般会产生明显的叶尖涡结构；在三维旋转主流流动的作用下，螺旋状发展的叶尖涡会对叶片产生比较强的诱导影响［3］。

如何准确捕捉风力机叶片上述流动结构是实现合理高效气动设计的前提。本文采用数值方法，获得了以NREL phase VI风力机叶片为原型的流场与叶尖涡结构的准确模拟结果，并与缩比模型的PIV实验结果形成了良好的对比。在此基础上，提出了基于多片小翼概念的分裂叶尖形式概念型水平轴风力机叶片设计方案，并针对其综合气动性能利用快速非支配排序遗传算法（NSGA－II）进行了多目标优化研究并获得了满足给定约束的优化结果。

1 数值模拟

1．1 模型与数值方法

水平轴风力机叶片流动具有明显的三维旋转和强烈的湍流特征。基于工程允许的计算能力，除了大涡模拟（LES）与脱落涡模拟（DES）方法外，数值求解雷诺平均Navier－Stokes（RANS）方程仍然是目前工程上能够兼顾湍流流动计算量和计算准确度的一种有效方法。本文采用该方法实现了风力机叶片基本流场的数值模拟。

由于暂不考虑侧滑等复杂风况，通过在上述区域中采用旋转坐标系求解三维不可压RANS方程，原始的非定常叶片绕流可以转化为新坐标系下的准定常流动进行求解。其控制方程形式在常规笛卡尔坐标系下的形式基础上应补充附加源项以考虑在非惯性系下的离心力与哥氏力影响。

根据叶片绕流的周向对称性，计算区域采用一半流场并根据低速不可压流动特性分别施加速度进口、压力出口，无滑移叶片物面以及周期边界条件，如图1所示。

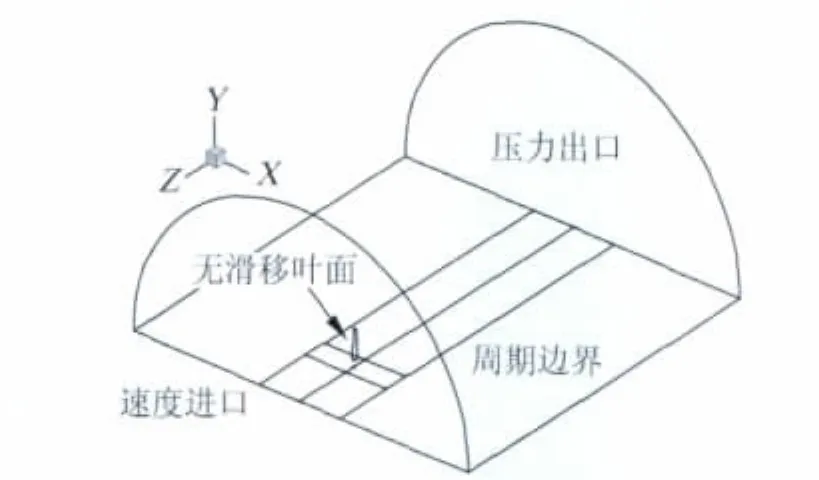
图1 风力机叶片流场计算区域Fig．1 Domain for the half flow field of a wind turbine blade

计算区域大小沿流向（图1中－z方向）为（－2R，8R），沿展向为5R（R为叶片长度）。总网格单元数超过6百万。为了在叶片下游区域计算网格局部加密以捕捉尾涡结构，总网格单元数接近2千2百万。

上述控制方程的离散形式通过有限体积法进行求解。其对流项采用二阶迎风格式，扩散项为中心差分。压力与速度的耦合采用SIMPLE算法实现［4］。RANS方程的封闭采用 Menter的k－ωSST模型［5］。

1．2 结果与讨论

利用上述方法对于原始NREL phase VI风力机叶片进行了计算，并与NREL盲比实验以及文献［2］中Sørensen等人的计算结果进行了对比，见图2。

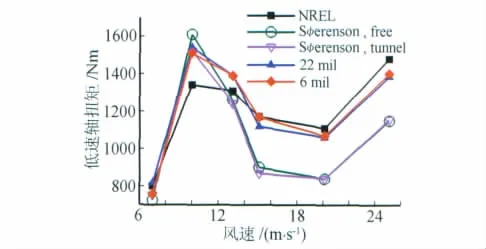
图2 低速轴扭矩结果对比Fig．2 Comparison of low－speed shaft torque

利用目前方法，尾流加密（22mil）和不加密（6mil）两套网格算得的低速轴扭矩结果在主要风速范围内与实验存在良好一致性。除10m／s之外主要计算结果与实验相对误差均在6%之内，说明对于该风力机叶片的整体性能把握较好。10m／s风速下出现较大偏差的主要原因是此风况下叶片吸力面边界层流动未完全分离，而目前所用RANS算法内尚未引入对于流动转捩位置的预估功能，因此导致该风速下对吸力面分离流动的影响把握不准。

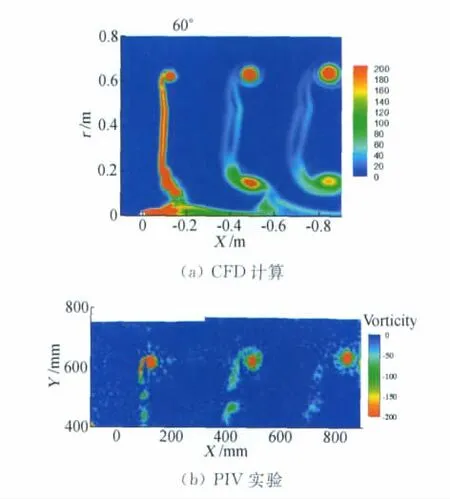
图3 尾流区涡量强度分布（周向角60°，风速12m／s，尖速比4．91）Fig．3 Vorticity in the wake（azimuth angle of 60°，wind speed of 12m／s，and tip speed ratio of 4．91）

在此基础上本文利用尾流区加密网格准确捕捉了近尾迹区叶尖涡的发展过程。图3中为与风洞PIV实验结果的对比。该实验设置的详细介绍见文献［6］。由图3可见，在给定风速下，计算得到的尾涡涡核位置与涡核强度与实验非常一致。

2 分裂叶尖布局设计

2．1 翼尖小翼概念

长期以来关于固定翼飞行器的研究表明，翼尖小翼能够有效的起到提高升力，抑制诱导阻力的效果。在此基础上基于多个小翼的分裂叶尖形式证明在机翼增升减阻方面具有更为优良的效果［7］。小翼设计在风力机叶片的设计中在近年来也得到了应用［8］。本文提出了基于多片小翼概念的分裂叶尖形式概念型水平轴风力机叶片设计方案，以研究该布局对于风力机叶片气动性能的控制效果。其基本形式如图4所示。

2．2 分裂叶尖数值模拟

作为初步设计，在原始叶片85%展长位置改为由三段相互独立的小翼组成的分裂叶尖布局。各小翼均无扭转，梢根比均为0．75，后掠角均为45°，从前缘向后缘上反角依次为40°，20°，0°。

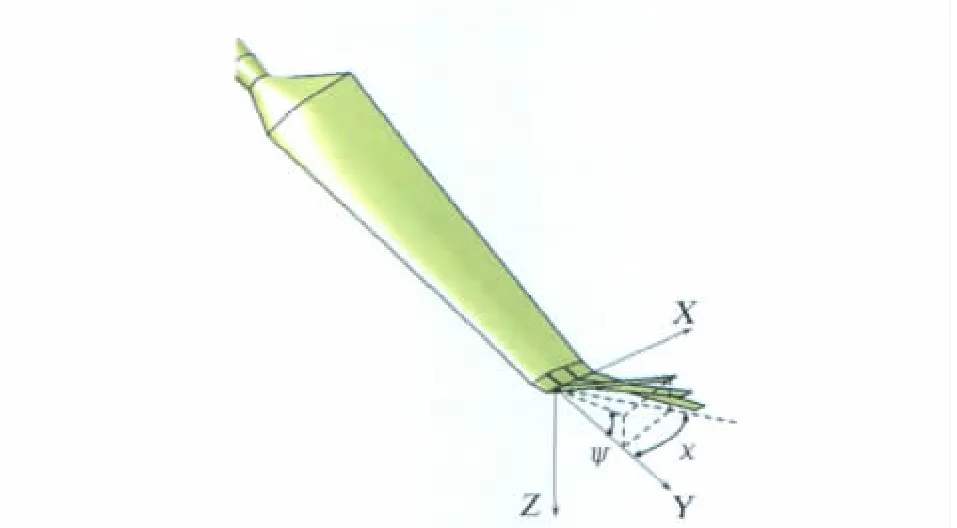
图4 带三个小翼的NREL phase VI叶片模型Fig．4 NREL phase VI model with three winglets

由于采用分裂叶尖形式的气动布局，多个小翼将原来集中于叶尖附近的环量进行了重新分配。图5中所示下游近尾迹区涡核附近的涡量极值随尾迹周向角的分布情况描述了这种重新分配环量的效果。分裂叶尖的布局（见图5中winglet1结果）使得近尾迹区涡核附近的涡量极值比原始叶片（见图5中basic结果）大为降低，从而有效减弱下游集中涡的诱导作用。

图5 尾流区涡量极值沿周向角的分布Fig．5 Azimuthal distribution of vorticity maximum in the wake

另一方面，各小翼的厚度均接近6%，且带有大后掠角，这种设计使得在中等和大风速下叶片吸力面在前缘附近获得更大的吸力峰（如图6中winglet1黑线所示），并体现为相应风速下轴扭矩输出的明显增长，在10m／s－25m／s范围内，增长幅度在7%－40%之间，见图7中winglet1结果。

图6 分裂叶尖布局80%展长位置压力分布，25m／sFig．6 Pressure distribution at 80%span，25m／s

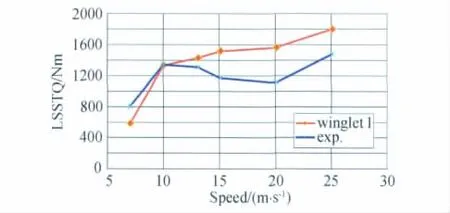
图7 分裂叶尖布局低速轴扭矩Fig．7 Low－speed shaft torque of the blade with multiple winglets

3 数值优化

在上述工作基础上，对叶片关键几何参数利用快速非支配排序遗传算法（NSGA－II）进行了多目标数值优化。为问题简化考虑，优化风速定为20m／s，小翼根稍比均为0．75。

该优化问题中需对以下两目标函数最小化：

其中Cp为风能利用系数，CT为轴向推力系数。由于CFD方法所需计算量过大，优化部分的上述目标函数采用自由涡尾迹方法计算得出，具体算法见文献［10］。

优化变量及约束条件为：

小翼上反角（向吸力面方向为正）：

小翼扭角：

3．1 遗传算法

快速非支配排序遗传算法（Fast and Elitist Nondominated Sorting Genetic Algorithm，NSGAII）是Deb等人于2002年在对NSGA算法进行了大幅改进的基础上提出的一种高效分类排序算法［9］。该算法引入了Pareto支配关系和个体分布评价函数，从而可以将复杂多目标优化问题转化成可比较个体优劣的单目标优化问题，能够用于进行任意目标个数的数值优化工作。该算法根据Pareto支配关系对种群内个体首先进行非支配分层以确定各个个体的层级；再用拥挤距离评价函数控制各个层级个体分布；然后用个体的层级个体之间距离做选择操作，并结合传统遗传算法的其它操作过程，最终得到Pareto最优解集。

3．2 结果与讨论

优化种群大小选取为36，迭代次数300次。得到的Pareto最优解集分布如图8所示。利用自由涡尾迹方法算得的基本型NREL PHASE VI叶片的风能利用系数Cp与轴向推力系数CT分别为0．02286和0．1635。比较发现，目前得到的优化解风能利用系数分布均明显高于该参考值，相对提高27%～31%不等；同时轴向推力系数CT与NREL PHASE VI原型叶片相比变化不大。

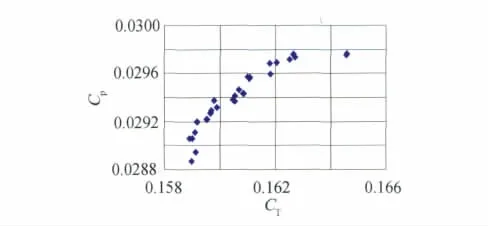
图8 Pareto最优解集分布Fig．8 Pareto solution sets

由NSGA－II算法得到的上述最优解集在给定目标函数空间中给出了一组满足相应约束条件的最优解，由于该解集任一个最优解并不更优于其他解，因此在最终的优化方案取决于研究者根据问题性质的具体分析与着眼点。由图8得知，在目前的优化范围内，随着风能利用系数的提高，一般伴随有轴向推力的增长。选取三个典型状态如表1所示，并分别对应于轴向推力最小、折中、能量转化率最大三个考虑因素。

4 结 论

借助于准确的数值模拟方法得知，分裂叶尖形式气动布局能够有效地分散风力机叶尖涡量的分布，从而减小其诱导影响；通过合理布置小翼，能够使叶片端部区域在中等和大风速下获得额外的前缘吸力，实现更高的气动效率，并为进一步在此风速范围的气动控制策略提供可行的技术准备。

基于NSGA－II遗传算法的优化方法能够在给定的性能约束范围内给出准确的全局最优解分布。对于上述问题，在不明显增大轴向推力的前提下，以风能利用系数形式给出的气动效率得到明显改善，比原始设计提高达30%左右。以上讨论表明，NSGA－II遗传算法与自由涡尾迹方法结合，是一种行之有效的风力机叶片气动性能优化方法。

［1］ HAND M M，SIMMS D A，FINGERSH L J，et al．Unsteady aerodynamics experiment phase VI：Wind tunnel test configurations and available data campaigns［R］．NREL／TP－500－29955，NREL，2001．

［2］ SØRENSEN N N，MICHELSEN J，SCHRECK S．Navier－Stokes predictions of the NREL phase VI rotor in the NASA Ames 80ft×120ft wind tunnel［J］．Wind Energy，2002，5（2－3）：151－169．

［3］ VERMEER L J，SORENSEN J N，CRESPO A．Wind turbine wake aerodynamics［J］．Progress in Aerospace Sciences，2003，39（6－7）：467－510．

［4］ VERSTEEG H K，MALALASEKERA W．An introduction to computational fluid dynamics－the finite volume method［M］．2nd Ed．，Pearson Education Limited，2007

［5］ MENTER FR．Two－equation eddy－viscosity turbulence models for engineering applications［J］．AIAA Journal，1994，32（8）：1598－1605．

［6］ 肖京平，武杰，陈立，史喆羽，风力机叶尖涡尾迹结构PIV测量实验研究［J］．应用数学和力学，2011，32（6）：683－692．

［7］ 陈明岩，齐孟卜，翼尖帆片的增升减阻研究［J］．航空学报，1994，15（6）：641－646．

［8］ JOHANSEN J，SORENSEN N N．Aerodynamic investigation of winglets on wind turbine blades using CFD［R］．Risø－R－1543（EN），2006．

［9］ DEB K，PRATA P A，AGARWAL S，et al．A fast and elitist multi－objective genetic algorithm：NSGA－Ⅱ［J］．IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197．

［10］许波峰，王同光．基于自由涡尾迹法和面元法全耦合风力机气动特性计算［J］．南京航空航天大学学报，2011，43（5）：592－597．