基于自由涡尾迹和遗传算法的叶尖小翼气动优化设计
2013-08-21许波峰王同光张震宇
许波峰,王同光,张震宇,王 珑
(南京航空航天大学 江苏省风力机设计高技术研究重点实验室,江苏 南京 210016)
0 引 言
风力机叶尖小翼能够提高风力机的输出功率,改变风轮的流场特性。风力机叶片旋转时,由于叶尖压力面和吸力面的压力差,气流会由压力面绕过尖部端面流入吸力面,形成复杂的三维流动,同时还会产生高强度的叶尖涡。叶尖涡使得叶片效率降低、疲劳载荷增加和叶尖噪声增大。这种现象在风力机叶片及飞机机翼上普遍存在。早在19世纪末就提出翼尖安装垂直板可以明显减轻三维效应从而减小诱导阻力[1]。风力机叶尖加小翼的想法最早由Van Holten(1976)[2]提出。Shimizu Y 等人[3]开发出一种 Mie型叶尖小翼,成功应用在小型风力机发电机上,动力输出增加10%-20%。Johansen J等人[4]研究了分别利用扭转和后掠的叶尖小翼提高风力机叶片效率的方法。国内内蒙古工业大学在Mie型小翼的基础上进行了叶尖小翼的实验研究[5]和数值模拟研究[6]。
本文优化设计的叶尖小翼为分裂式,以NREL PhaseⅥ叶片为设计对象。考虑到CFD方法的计算量大而遗传算法又是要以大量个体计算为基础,本文采用自由涡尾迹(FVW)方法[7-8]对小翼叶片建模,计算叶片的气动性能。以风能利用系数最大和风轮推力系数最小为目标,采用快速非支配排序遗传算法[9](NSGA-Ⅱ),通过不断遗传叶尖小翼的形状参数,搜索满足多目标优化的Pareto最优解集。
1 数学模型
1.1 设计变量
分裂小翼的俯视图和左视图如图1所示,从前缘至后缘三个小翼顺联排布,小翼根稍比均为0.75,有相同的后掠角χ,由前往后小翼上反角分别为Ψ1、Ψ2、Ψ3,每个小翼都具有不同的扭角分布。上反角等于0°时,小翼在叶片展向的投影长度为0.59m,保证叶片总长度与NREL PhaseⅥ叶片相同。
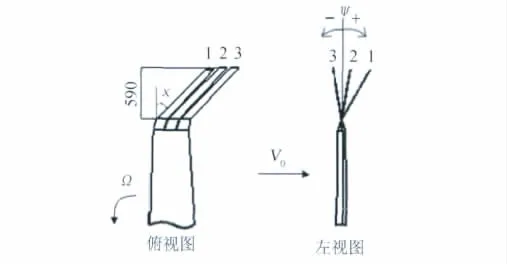
图1 小翼布局示意图Fig.1 Schematic diagram of winglet
叶片主体部分的翼型为S809,小翼的翼型为NACA0006。定义各参数的正负和取值范围:后掠角向后缘方向为正,且0°≤χ≤60°;上反角向吸力面方向为正,且-30°≤Ψ3≤Ψ2≤Ψ1≤60°;扭角定义前缘低头为正,三个小翼扭角分布分布满足

1.2 目标函数
分裂小翼可以减轻三维效应,且能使叶尖涡破碎,从而减小诱导阻力。叶片载荷越大,通过小翼性能提高越明显。确定小翼优化的设计风速为20m/s。设计目标为风能利用系数最大和风轮推力系数最小,即

式中,CP为风能利用系数,CT为风能推力系数,NG为总的迭代代数。
2 求解方法
2.1 自由涡尾迹模型
对风力机流场作不可压和位流假设,气动模型可以简化为来流、附着涡线和自由涡面的总和。尾迹建模如图2所示,叶片主体和小翼均离散成多个叶素段,附着涡线和控制点均在1/4弦线上,从叶素边界尾缘拖出涡线组成自由涡面。
自由涡尾迹方法允许涡线节点随当地流速自由移动,从而建立涡线的偏微分控制方程。将计算域在时间(Ψ)和空间(ζ)上离散,对控制方程作五点中心差分离散,并取Δψ=Δζ,则涡线控制方程可以简化为
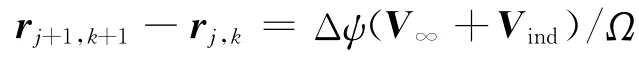
式中,V∞是来流速度,Ω是风轮旋转速度,Vind是涡线对当前节点的诱导速度总和。计算诱导速度运用了Biot-Savart定律,为了避免直线涡元计算出现奇点,且考虑涡的粘性耗散效应,涡核半径随时间渐渐增大,变化方式与Lamb-Oseen涡核形式一致,为
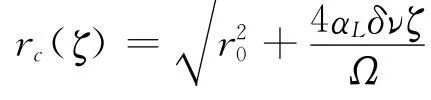
式中,r0是初始涡核半径,αL、δ和ν均为常数。尾迹迭代过程中,引入松弛因子来修正涡线节点位置

本文中,上式的松弛因子ω等于0.5。每步迭代后,计算相邻两步的尾迹形状的均方根,当均方根小于10-4表示尾迹收敛。

图2 尾迹分析示意图Fig.2 Schematic diagram of wake analyse
利用收敛的尾迹求解叶片附近的流场信息,根据叶素气动理论求出叶片的分布载荷以及总体气动性能。
2.2 NSGA-Ⅱ算法
快速非支配排序遗传算法(NSGA-Ⅱ)是对NSGA算法进行大幅改进的一种高效分类排序算法,其通过引入Pareto支配关系和个体分布的评价函数,将复杂的多目标优化问题转化成一类可以比较个体优劣的单目标优化问题,适用于任意目标数的优化问题。
新算法主要在以下三个方面对NSGA算法加以改进:一、通过使用一种快速的非支配分类排序方法,将目标数为M,种群大小为N的计算复杂度降低;二、采用拥挤度评价方法取代适应度共享函数法,改善个体分布的均匀性;三、加入了精英保存策略以改善算法的鲁棒性和收敛速度。
NSGA-Ⅱ算法流程见图3,其中,采用拥挤距离方法作为评估种群分布的主要方法,定义每一层中个体前后相邻两点之间在各个目标方向上的距离之和为评价函数;采用快速非支配排序法根据个体非劣解的层次关系对种群划分级别;按照先层级再拥挤距离的顺序对个体进行选择操作,选择出新的父代种群,再通过遗传变异得到第i+1代种群。
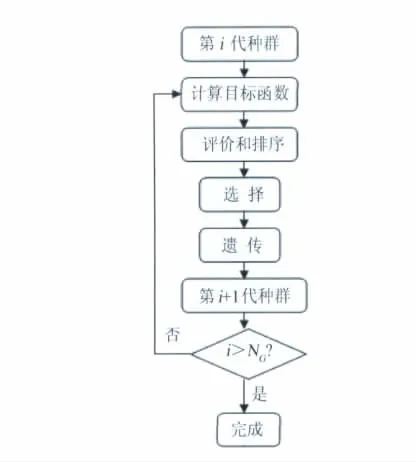
图3 NSGA-Ⅱ算法流程图Fig.3 Flowchart of NSGA-Ⅱ
3 计算结果与分析
以NREL PhaseⅥ叶片为设计对象,先计算原始叶片的气动性能,与实验值做对比,验证FVW方法的准确性。再使用FVW/NSGA-Ⅱ耦合方法,对小翼形状进行优化。
3.1 气动模型验证
图4为在不同风速下的风轮低速轴扭矩,实心点为实验结果,空心点为FVW模型计算结果。计算结果与实验结果在各个风速下吻合度都较好。15m/s和20m/s风速计算与实验结果存在相反的偏差,这是由于在高风速下叶片大部分剖面都处于失速甚至深失速状态下,很难准确模拟翼型的气动数据,而这是准确模拟叶片性能的关键。更大风速25m/s计算与实验结果又很一致可能是一种巧合。从模拟结果可见,FVW模型能够较准确的模拟叶片的气动性能,可以为NSGA-Ⅱ方法提供可靠的性能目标。

图4 低速轴扭矩比较Fig.4 Comparison of low speed shaft torque
3.2 优化结果
小翼的优化设计采用风能利用系数CP最大和风轮推力系数CT最小的两目标方案,种群大小为36,迭代次数为300。

表1 计算状态Table 1 Computational parameters
图5给出优化得到的分裂小翼叶片的Pareto最优解的分布图。两目标优化的最优解并不是唯一解,而是一个解集,且近似分布在一条二次曲线上,推力系数随着风能利用系数的增大而增大。原始叶片(原NREL叶片)用同样的方法计算CP和CT,计算结果分别为0.02286和0.1635。加小翼的优化结果CP最大能达到0.02977,相比原始叶片提高了30%,且CT与原来相当。可见加小翼的叶片气动性能会有大幅提高。决策者可以根据意愿和工程需要从Pareto最优解中选择小翼的形状:若要追求成本最小化,可以选择A解的小翼形状;若要追求发电量最大化,可以选择C解;若要两者折中考虑,可以选择B解。

图5 Pareto最优解分布Fig.5 Distribution of the Pareto-optimal solution
使叶片性能最优化的小翼形状具有一定的规律性,图6~图8给出最优解的几何形状分布。图6中显示,最优后掠角基本都在20°附近,当要求高的风能利用系数时,后掠角会增大至50°左右。从图7可以看出:三者满足约束条件Ψ3≤Ψ2≤Ψ1;1号和2号小翼的上反角均在55°至60°之间,3号小翼的上反角则在正负10°范围内;总有两个小翼的上反角很接近。三个小翼的扭角约束参数A和B优化结果均比较接近,A在16与20之间,B则在1.5与2之间。取图5中的B解得到图8的扭角的径向分布,小翼根部扭角与叶片主体连接段一致,达到光滑过渡的目的。扭角的径向变化率约等于6°/m,且变化趋势与主体部分相反。这些小翼形状规律对于今后小翼的设计及改型有很好的指导性作用。

图6 后掠角分布Fig.6 Distribution of sweepback

图7 上反角分布Fig.7 Distribution of dihedral angle

图8 B解的扭角径向分布Fig.8 Radial distribution of twist angle in solution B
4 结 论
采用FVW/NSGA-Ⅱ耦合方法,对风力机叶尖分裂小翼的几何形状优化设计进行研究。通过与实验结果的对比,证明FVW方法计算叶片气动性能的可靠性。耦合方法优化得到一个Pareto最优解集,且分布在一条曲线上,在推力系数相当的情况下,风能利用系数与原始叶片比较能够提高近30%。小翼的几何形状在最优解集下分布具有一定的规律性,这对于今后小翼的设计及改型有很好的指导性作用。
[1] JUPP J.Wing Aerodynamics and the science of compromise[J].Aeronautical Journal,2001,105(1053):633-641.
[2] VAN HOLTEN.Windmill with aiffuser effect induced by small tip vanes[A].In:International Symposium on Wind Energy Systems[C],Camdridge,UK:1976.
[3] SHIMIZU Y,VAN BUSSEL G J,MATSUMURA S,et al.Studies on horizontal axis wind turbines with tip attachments[A].EWEC'90Conference proceedings[C],Madrid,Spain:1990:279-283.
[4] JOHANSEN J,GAUNAA M,SORENSEN N N.Increased aerodynamic efficiency on wind turbine rotor using winglets[A].26th AIAA Applied Aerodynamics Conference[C].Hawaii,USA:2008:12-21.
[5] 东雪青,汪建文,韩晓亮,等.风力机叶尖加小翼流场的试验研究[J].工程热物理学报,2009,30(10):1162-1164.
[6] 贾瑞博,汪建文.小翼对水平风力机流场特性的改变[J].华北电力大学学报,2010,37(5):83-87.
[7] 许波峰,王同光.基于自由涡尾迹法和面元法全耦合风力机气动特性计算[J].南京航空航天大学学报,2011,43(5):592-597.
[8] WANG T G,WANG L,ZHONG W,et al.Large-scale wind turbine blade design and aerodynamic analysis[J].Chinese Science Bulletin,2012,57:466-472.
[9] DEB K,PRATA PA,AGARWAL S,et al.A fast and elitist multi-objective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
