货物列车运行引起的大地振动及其对精密仪器的影响＊

张鹏飞，雷晓燕，高亮，刘庆杰

(1.北京交通大学 土木建筑工程学院，北京 100044;2.华东交通大学铁路环境振动与噪声教育工程研究中心，江西 南昌 330013)

近年来，铁路和城市轨道交通在我国得到了快速发展，轨道交通引起的环境振动问题引起了政府和民众的普遍关注。铁路环境振动会对居民的日常生活和工作、古建筑的结构安全以及工厂、学校内精密仪器设备的生产和使用产生很大的影响［1］。为了解决轨道交通引起的环境振动问题，国内外学者进行了大量的研究工作。Sheng等［2－6］采用解析的波数－频率域法建立了轨道结构单层或多层梁模型，分析了高速列车引起的轨道和大地振动。国外学者［7－8］对精密仪器的环境振动标准进行了详细讨论，Xia等［9－11］对地铁列车运行引起的振动对精密仪器的影响作了大量的现场测试和理论分析工作，这些研究取得了很多成果，得出了大量有意义的结论。本文以新建龙烟铁路沿线附近厂房内的精密仪器为研究对象，利用有限元法，建立轨道—桥梁及桥墩－基础－大地的计算模型，利用这2个模型计算货车在不同运行速度下引起的大地振动响应，得出振动加速度、速度及位移沿距离的衰减规律，分析铁路环境振动对沿线厂房内精密仪器的影响。

1 背景资料

1.1 龙烟铁路概况

龙烟铁路西起大莱龙铁路的龙口西站(不含)，经龙口市、蓬莱市、经济开发区、福山区、芝罘区至珠玑站，新建正线全长112.735 km;福山联络线13.166 km。与规划德大铁路、既有大莱龙铁路共同形成太原煤炭基地至环渤海港口烟台(龙口)港的便捷通道，是环渤海铁路、沿海铁路的重要组成部分。线路为Ⅰ级单线(预留双线条件)铁路，旅客列车采用城际动车组，最高运行速度为160 km/h，货物列车采用SS4和HXD1型电力机车牵引，最高运行速度为120 km/h，全线采用有砟轨道。

1.2 精密仪器

在烟台开发区，龙烟铁路以高架形式近距离经过烟台胜利汽车零部件制造有限公司，该公司内设有两台精密仪器－光谱仪和制芯机，根据线路设计平面图和现场测量，光谱仪到线路中心线的垂直距离为96.93 m，振动参数限值要求如下:加速度＜1.98 m/s2;速度 ＜8 ×10－3m/s;位移 ＜8 ×10－5m;制芯机到线路中心线的垂直距离为124.75 m，振动参数限值要求如下:x和y方向的加速度 ＜1.15 m/s2，z方向的加速度 ＜0.8 m/s2。

2 有限元模型

为模拟列车运行产生的振动，建立轨道－桥梁耦合有限元模型，将车辆(机车)简化为一系列以速度v移动的荷载，计算作用于桥梁支座上的反力，建立桥墩－基础－大地三维有限元模型，将第1个模型计算的力加载到第2个模型上，计算与线路中心线不同距离的地面振动加速度、速度和位移。

2.1 有限元振动计算理论

利用有限元方法进行结构振动计算，可以得到在移动荷载作用下结构随时间变化的节点加速度、速度和位移的响应，基本方程为:

式中:［Me］，［Ce］和［Ke］分别为结构质量矩阵、阻尼矩阵和刚度矩阵;{}，{}和{u}分别为e结构振动加速度、速度和位移;{Fe}为荷载向量。对于上述微分方程的求解可采用Newmark时间积分方法在离散的时间点上求解动力学方程，系统采用Raleigh阻尼。

2.2 轨道－桥梁有限元模型

该模型从上到下依次为:60 kg/m钢轨、扣件、轨枕、道砟、桥梁。

钢轨采用梁单元Beam3来模拟，轨枕用质量点单元Mass21等效，垫板、扣件以及道床可以采用弹簧阻尼单元combin14等效。轨道－桥梁有限元力学模型如图1所示。

图1 轨道－桥梁有限元力学模型Fig.1 Track－bridge finite element mechanics model

根据一般轨道的实际支撑情况取钢轨梁单元的长度为0.6m，钢轨的每个节点处用弹簧阻尼单元连接一个轨枕质量点单元，再由弹簧阻尼单元连接到桥梁节点上。模型的参数取值见表1。

2.3 桥墩—基础—大地有限元模型

桥墩—基础—大地模型考虑5跨简支梁桥，桥墩尺寸由线路设计单位提供。

桥墩及承台采用solid45单元，最小单元尺寸0.5 m;桩基础采用beam4模拟，桩顶单元的节点与承台节点耦合，为方便计算，桩长均设为42 m，大地边界采用粘弹性吸收边界，用以吸收边界上的反射波［12］。桥墩－桩基础模型如图2所示，桥墩－基础－大地有限元模型如图3所示，土层参数由线路勘探设计单位提供，见表2。

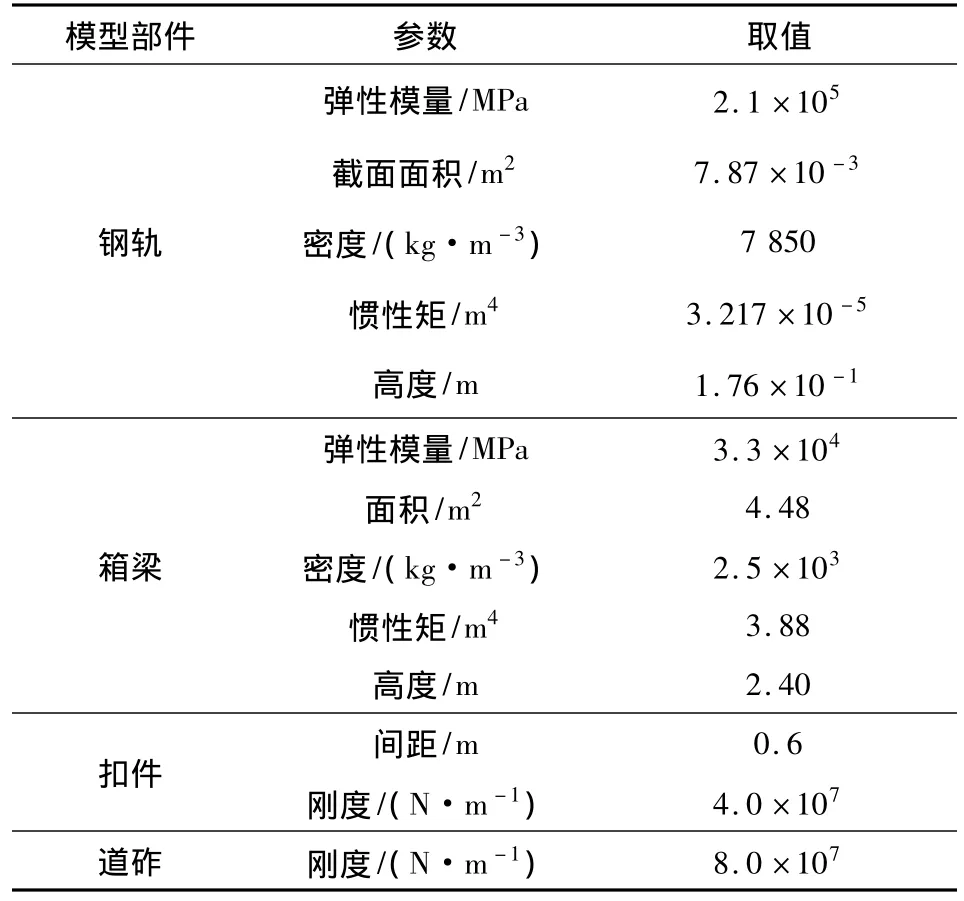
表1 轨道－桥梁模型参数表Table 1 Track－bridge model parameters

图2 桥墩－桩基础有限元模型Fig.2 Pier－ pile foundation finite element model

图3 桥墩－基础－大地有限元模型Fig.3 Pier－foundation－ground finite element model

表2 土层参数表Table 2 Soil parameters

3 计算工况

为了模拟振动最不利的情况，计算时考虑两列货车在烟台胜利汽车零部件制造有限公司处交会，货车速度分别取120，100及80 km/h。各计算工况见表3。

表3 计算工况Table 3 Calculation modes

4 计算结果分析

4.1 桥墩支座反力计算

在高架轨道诱发环境振动的研究中，车辆(机车)的振动并不是主要考虑因素，因此将其简化为一系列以速度v移动的荷载。在考虑轨道不平顺对轮轨力的影响时，可以将不平顺导致的惯性力叠加在轮对静荷载上，轨道不平顺采用美国6级不平顺谱样本，如图4所示。整个分析计算过程采用全瞬态的分析方法，时间积分步长取为0.005 s，计算的总时间7.8 s。为取得有效的计算精度，整列车的车辆数取为8节。

图4 不平顺样本Fig.4 Irregularities samples

利用轨道—桥梁模型，带入表1中的参数，可以得到3种工况下的桥墩支座反力，如图5～7所示。

图5 工况1桥墩支座反力Fig.5 Piers supporting force of Mode 1

图6 工况2桥墩支座反力Fig.6 Piers supporting force of Mode 2

4.2 振动传播规律分析

图7 工况3桥墩支座反力Fig.7 Piers supporting force of Mode 3

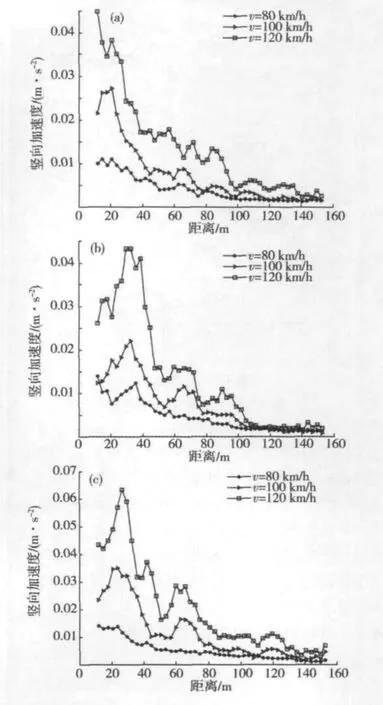
图8 加速度沿距离的变化曲线Fig.8 Acceleration curve along the distance

图9 速度沿距离的变化曲线Fig.9 Speed curve along the distance

将桥墩支座反力计算结果加载到桥墩－基础－大地有限元模型中，采用瞬态分析方法对距离线路中心线不同位置的地面振动进行分析，图8～10所示为各工况振动加速度、速度及位移沿距离的变化规律曲线。从图8～10可以看出:货物列车速度对振动响应的影响较大，速度越高，地面上相同位置上的振动响应越大;各工况振动指标沿距离衰减特性基本一致，呈现指数曲线的衰减规律，在距离线路中心线80 m左右的范围内，振动迅速衰减，但在20－40 m范围内有振动“反弹增大”现象出现，超过80 m之后，振动表现为缓慢衰减的趋势。

4.3 振动对精密仪器的影响分析

光谱仪与线路中心线之间的距离为96.93 m，分别提取光谱仪位置处各工况下的振动加速度、速度和位移，见表4。制芯机与线路中心线之间的距离为124.75 m，分别提取制芯机位置处各工况下的振动加速度、速度和位移，见表5。

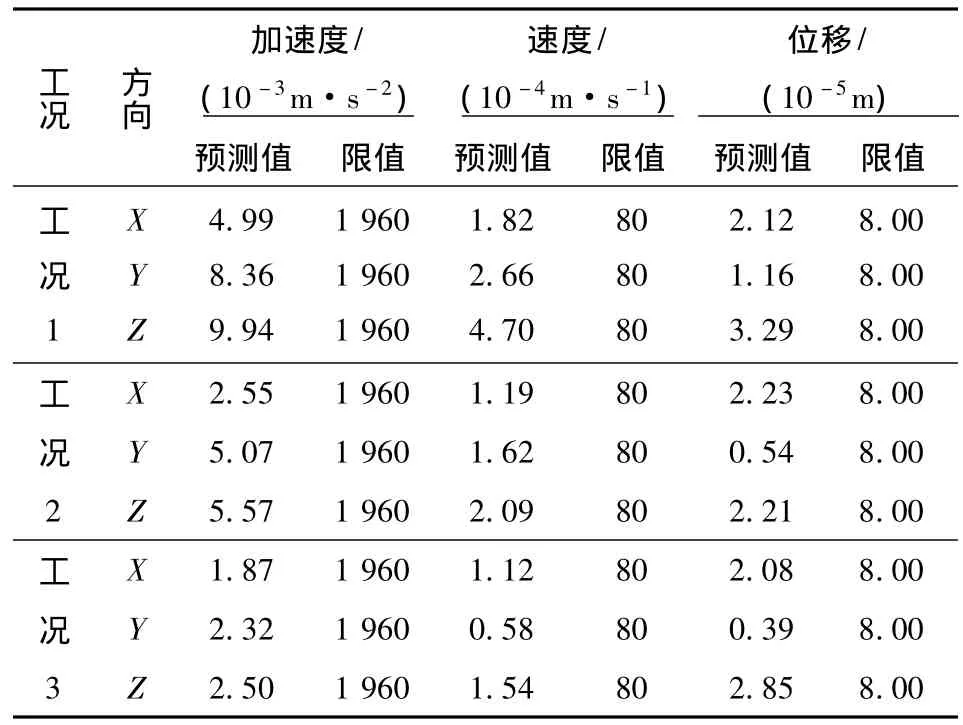
表4 光谱仪的振动参数值Table 4 Spectrometer vibration parameters

表5 制芯机的振动参数值Table 5 Core－making machine vibration parameters

从表4和表5可以看出:当2货车以120，100和80 km/h的速度在精密仪器附近交会时，光谱仪的加速度、速度及位移的预测值满足仪器振动限值要求;制芯机的加速度预测值满足仪器的限值要求。

5 结论

(1)货物列车速度对振动响应的影响较大，速度越高，地面上相同位置上的振动响应越大。

(2)振动加速度、速度和位移沿距离的衰减特性基本一致，呈现指数曲线的衰减规律，在距离线路中心线80 m左右的范围内，振动迅速衰减，但在20～40 m范围内有振动“反弹增大”现象出现，超过80 m之后，振动表现为缓慢衰减的趋势。

(3)当两货车以120，100和80 km/h的速度在精密仪器附近交会时，光谱仪的加速度、速度及位移的预测值满足仪器振动限值要求;制芯机的加速度预测值满足仪器的限值要求。

［1］Crispino M，Dapuzzo M.Measurement and prediction of traffic－ induced vibrations in a heritage building［J］.Journal of Sound and Vibration，2001，246(2):319 －335.

［2］Sheng X，Jones C J C，Petyt M.Ground vibration generated by a load moving along a railway track［J］.Journal of Sound and Vibration，1999，228(1):129 －156.

［3］Picoux B，Houedec D L.Diagnosis and prediction of vibration from railway trains［J］.Soil Dynamics and Earthquake Engineer－ing，2005(25):905 －921.

［4］谢伟平，胡建武，徐 劲.高速移动荷载作用下的轨道－地基系统的动力响应［J］.岩石力学与工程学报，2002，21(7):1075 －1078.XIE Weiping，HU Jianwu，XU Jin.Dynamic response of track－ground systems under high speed moving lord［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21(7):1075 －1078.

［5］边学成，陈云敏.列车荷载作用下轨道和地基的动响应分析［J］.力学学报，2005，37(4):477 －484.BIAN Xuecheng，CHEN Yunmin.Dynamic analyses of track and ground coupled system with high－speed train loads［J］.Chinese Journal of Theoretical and Applied Mechanics，2005，37(4):477 －484.

［6］雷晓燕.高速列车诱发地面波与轨道强振动研究［J］.铁道学报，2006，28(3):78 －82.LEI Xiaoyan.Study on ground waves and track vibration boom induced by high speed trains［J］.Journal of the China Railway Society，2006，28(3):78 －82.

［7］Amick H.On generic vibration criteria for advanced technology facilities［J］.Journal of the Institute of Environmental Sciences，1997，40(5):35 －44.

［8］Gordon C G.Generic vibration criteria for vibration sensitive equipment［C］.Proceedings of the 1999 Optomechanical Engineering and Vibration Control.Denver，Colorado，USA:Society of Photo－Optical Instrumentation Engineers，1999:22 －33.

［9］Xia He.Vibration effects of light－rail train－viaduct system on surrounding environment［J］.Int J of Structural Stability and Dynamics.2002，2(2):227－ 240.

［10］马 蒙，刘维宁，丁德云，等.地铁列车振动对精密仪器影响的预测研究［J］.振动与冲击，2011，30(3):185－190.MA Meng，LIU Weining，DING Deyun，et al.Prediction of influence of metro trains induced vibrations on sensitive instruments［J］.Journal of Vibration and Shock，2011，30(3):185－190.

［11］栗润德，张鸿儒，刘维宁.地铁引起的地面振动及其对精密仪器的影响［J］.岩石力学与工程学报，2008，27(1):206－213.LI Runde，ZHANG Hongru，LIU Weining.Metro－induced ground vibrations and their impacts on precision instrument［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27(1):206－213.

［12］雷晓燕.城市轨道交通环境振动预测与评价［J］.城市轨道交通研究，2008(11):12－17.LEI Xiaoyan.Prediction and assessment of environment vibration induced by urban mass transit［J］.Urban Mass Transit，2008(11):12 －17.