扫雪问题之最短时间
2013-08-03陈兴婉
陈兴婉
一、问题重述
地图中实线表示马里兰州 (Maryland)威克米克市(Wicomico)清除积雪区域双行的道路,虚线是州高速公路。雪后,两辆扫雪车从地图*号标出的两点的每一地点以西约6.44(4mile)处出发清扫道路上的积雪。试为两车找出有效的路径。扫雪车可以通过高速公路进出市内道路。假定扫雪过程中车子不会损坏或停止,并且道路交叉处不需要附加扫雪程。

二、问题分析
要解决的问题是,为两台扫雪车设计出有效的路径进行威克米克市积雪道路的清扫工作。两辆扫雪车从地图*号标出的两点的每一地点以西约6.44km(4mile)处出发清扫道路上的积雪,市内的道路均为双向,扫雪车在道路的交叉点上可转向行驶。把道路的交点作为顶点集V,道路作为边集E,把所给地图定义为有向图,利用图论的知识进行分析,有向图D是强连通的,且每个顶点的入度等于出度,即有向图D是一个欧拉图,图中存在欧拉回路。
扫雪车遵守交通规则且靠右行驶,根据模型的假设,扫雪车经过路面一次就能把该单行道彻底地清扫干净,那么,扫雪车要完成任务就等于把所有的单向道路都至少行驶一遍。为了使扫雪车高效率地完成工作,考虑到两台扫雪车同时进行工作,根据模型假设,两扫雪车功率一样且作业过程以匀速进行,首先把地图分为南、北两个工作区,分别由两辆扫雪车负责。在两台车工作量相等情况下,设想其中一台扫雪车工作量减少一条道路,则另一台扫雪车的工作量将增加一条道路,即工作时间增长一个单位,使得工作效率下降。所以,尽量使得两工作区的工作量相近,即道路的总长相当,两扫雪车同时进行工作,结束时间相近,缩短工作时间。
另外,扫雪车的工作时间是由两部分组成的,即作业时间与空驾时间,工作时间即为扫雪用的时间,空驾时间即为行驶高速公路或清扫完毕的道路使用的时间之和。为了提高工作效率,实现扫雪车在完成任务的前提下,使得空驾时间最短。由于假定扫雪车是匀速行驶的,所以,要使得空驾时间最短就等于空驾的路程最短,尽量不走高速公路或清扫干净的道路。为了实现扫雪车不重复行驶道路,即把问题转化为图的遍历问题,经过所有的边一次且仅一次,经过所有的顶点。
三、问题假设与符号说明
(一)问题假设
1.扫雪车在作业的过程中不会出现突发状况使其停止工作;
2.扫雪车在开始工作到结束工作的过程中,燃油供应足够,不需要中途加油;
3.扫雪车在拐弯处不进行特殊的扫雪处理;
4.扫雪车在拐弯处的路程忽略不计;
5.扫雪车在高速公路上行驶不计入工作量;
6.扫雪车可在高速公路上任意行驶且在高速公路与市内公路接口处任意出入;
7.假设扫雪车经过路面一次即把该单向路面清扫彻底;
8.扫雪车作业过程中,已经停雪,清扫完的路面不会被落雪重新覆盖,且不涉及融雪问题;
9.扫雪车遵守交通规则,靠右行驶;
10.两扫雪车功率一样且作业过程以匀速进行;
11.假设高速公路上速度够快,并且无需扫雪。
(二)符号说明
表示第个顶点;表示第条边;表示顶点集;表示边集;表示由顶点集和边集组成的有向图;表示路程;表示速度。
四、模型建立与求解
1.模型引入。本题考察马里兰州威考密科县的双行马路有效扫雪问题,因此需要考虑车子如何行走路径最短,同时两车工作完的时间最短。
2.模型建立。该扫雪区域图考虑到图的复杂,除悬挂点外,每一点度数至少为2,因此,这里找出一条主干道,使得所有街道与其有关,并且用截断的方法将该县各街道转换为树的形式,再各自进行遍历,以得到该县的行走路径。为了使得扫雪路径更加有效率,因此我们必须考虑时间最优与路径最优。
根据计算,可知该扫雪区域每一节点的度数至少为2,因此可以在图上寻找一条主要干道,使得剩下的道路组合成为树形区域。
Step1:令两扫雪车相向而行,将该城镇横向主干道走完,直到到达彼此的出发点。同时此路线将该扫雪区域划分为几个树形图。
Step2:两车近似相等分工合作,将剩下的区域进行遍历,因为所得树形图不连通,因此需要用到高速公路出入口走完所有树。这里不考虑扫雪车在高速公路上所用时间。(结果如图2)
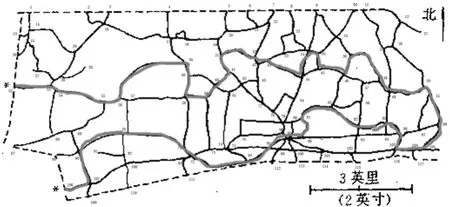
图2
3.模型求解。Step1:两辆扫雪车用在共同路径,即主干道上的路程与时间分别为:
Step2:将剩余区域等分为两段,使扫雪车共同工作时间最短。根据对图路径的计算,得知,当分界线为:7-22-32-42-63-77-78-79-76-75-94时,两边工作区域近似相等,左边扫雪车工作路程为:73.6英里,右边扫雪车工作路程为73.2英里。
Step3:用在高速公路上的时间为:(以高速公路限速为例)
4.模型检验。通过计算得到两辆车的路径分别为:
52-53-54-55-56-30-40-60-41-31-32-42-43-35-45-46-47-48-49-50-51-87-86-84-83-82-55-81-98-97-95-94-72-71-70-90-107-106-67-67-68-69-90-89-90-69-55-69-68-54-68-67-109-107-108-110-108-93-111-93-72-73-74-61-74-73-59-60-41-60-59-58-40-58-57-56-70-92-91-92-108-92-70-57-58-59-73-72-93-108-107-109-13-15-28-15-37-38-39-38-37-15-14-29-16-17-30-17-18-19-31-19-20-21-22-21-6-21-20-5-20-19-18-17-4-16-3-16-2-16-29-14-1-14-13
另一辆车的路径为:
52-54-55-56-30-40-60-61-62-41-31-42-43-33-34-35-45-46-47-48-49-50-51-88-87-86-84-83-82-65-81-98-97-95-75-95-97-99-112-99-97-101-100-113-100-101-97-101-114-101-102-115-102-103-116-103-104-117-105-88-51-88-87-88-105-104-103-102-83-98-83-102-101-97-80-79-64-78-44-43-44-34-23-33-23-8-23-34-9-24-36-24-36-46-65-66-82-85-84-85-86-85-49-25-26-50-26-12-27-12-26-25-11-25-49-85-83-66-47-66-65-46-36-48-36-24-10-24-9-34-44-45-44-64-79-80-97-100-99-95-94-72-71-70-90-107-106
通过比较得到两辆扫雪车的工作路径不重复,如下图所示。
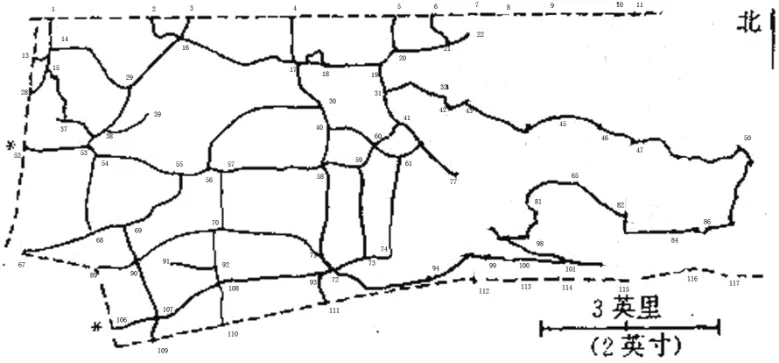
图3

图4
五、模型优缺点分析
模型优点:首先将城镇主要干道清理完毕,更加适合实际情况;将复杂的图转化为树。
模型缺点:需要用到高速公路出入,使得路程加长。
[1]屈婉玲,耿素云,张立昂.离散数学[M].北京:高等教育出版社,2008
[2](美)KennethH.Rosen.离散数学及其应用[M].北京:机械工业出版社,2007
[3]朱振元,朱承.数据结构——C++语言描述[M].北京:清华大学出版社,2007
