一种改进的等效系统拟配方法
2013-07-25裴彬彬徐浩军张峰刘东亮方标兵
裴彬彬,徐浩军,张峰,刘东亮,方标兵
(1.空军工程大学航空航天工程学院,陕西西安 710038;2.陕西飞机工业集团飞机设计研究院,陕西汉中 723213;3.中国人民解放军95183部队,湖南 邵东 422801)
0 引言
对一架未增稳的常规飞机,其纵向和横向的典型模态是容易区分的,可以直接与有关的规范进行比较,并进行飞行品质评定。但对于使用了电传操纵系统的高阶增稳飞机,系统中包括有反馈、前馈及中频成形滤波器和其他高频部件等,其阶次可高达50~70阶[1],其中很多附加模态难以与飞机的典型模态相区分,无法按照常规飞机的评价准则对其进行飞行品质评价。根据MIL-F-8785C可以用等效系统的方法找到一个低阶动态模型来代替高阶系统,使它与高阶系统具有相同的飞行品质评价。
对等效拟配问题的研究已取得一些相关成果,其中对各种最优化算法及其改进算法在等效系统拟配中的应用研究较多,如文献[2-3]采用不同的算法在一定程度上解决了运算速率及避免陷入局部最优解的问题。
本文提出了一种基于遗传算法的带加权因子的等效系统拟配方法,不仅具有很高的拟合精度,而且失配参数的分布显得十分合理,具有较高的工程应用价值。
1 等效系统拟配基本原理
1.1 遗传算法
对于大部分最优化算法在等效系统拟配中的应用而言,一般需要确定拟配的初值。初值的选取关系到能不能收敛到最优解。这些初值一般通过经验估算,但仍需进行多次的试凑,较为复杂,工作量较大,而遗传算法在这方面具有极大的优势。
采用遗传算法进行等效系统拟配,不需要确定拟配参数的初值,可以将优化解限定在要求的范围之内,从而避免了不合理解的出现[4-5]。此外,由于遗传算法的结果具有随机性,利用遗传算法进行求解,所得的最优化参数大多并不相同,经验表明[1]:每一个“拟合”良好的等效系统都能得到同样的飞行品质评价结果。基于这些特点,遗传算法在等效系统拟配计算中有很好的应用前景。
遗传算法进行等效拟配的具体计算步骤如下:
(1)确定拟配参数的范围。具体参数的范围依据飞行品质规范中的等级要求来确定,从而将参数限定在一个较为合理的区间内。
(2)确定初始种群。初始种群采用随机方法选取,该方法产生的种群具有随机性、全面性,避免了局部最优解的问题。初始种群数目越大,对整个解空间的代表性越强,防止早熟收敛的能力也越强,但计算量也越大。
(3)确定适应度函数。适应度函数的形式为:
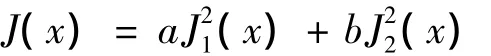
式中,a,b为加权系数;J(x)为与目标函数相关的函数。
(4)确定遗传算子参数和优秀个体数目。
(5)迭代运算。将初始种群经过遗传运算生成的个体作为新的父代个体,重复运算。退出迭代运算时,当前父代个体中的优秀个体就是运算的结果。
1.2 等效拟配过程
已知高阶增稳飞机的频率特性为GHOS(jω),并给定低阶等效经典飞机的频率特性表达式GLOS(jω),寻求GLOS(jω)中的有关参数,使下述目标函数最小:

式中,M为失配参数;K为幅值差与相角差之间的加权系数(物理上表示1 dB的幅值差与7°的相角差在总的失配中有相等的重要意义),通常K=0.016~0.020(常用 0.0175);ΔG(jω)为取自ω1~ω2之间给定离散点上高阶系统与低阶系统频率特性的幅值差;ΔΦ(jω)为相应的相角差。
要对飞机飞行品质给出准确评价的关键是如何在线性范围内寻求到与高阶动力学特性相类似的低阶系统。对于低阶等效系统的拟配问题,研究者已经做了大量的工作,针对不同特性的飞机提出了各种拟配模型。以纵向的俯仰角速率进行拟配为例,依据 GJB 2874[6]及 MIL-HDBK-1797[7],对于常规响应类型的飞机纵向通道,给定的俯仰角速率的低阶等效模型为下述经典飞机的传递函数:

式中,e-τs在进行参数辨识时对纯延迟环节作一阶伯德近似描述[8]。
通常的做法是取ω1=0.1 rad/s,ω2=10 rad/s,且在频率对数坐标轴上按均匀等分取20个点对上述低阶等效系统的参数利用遗传算法等最优化算法进行求解。拟配过程中这种做法在0.1~10 rad/s的频率范围具有较高的拟配精度,但是根据GJB 2874中对失配包络曲线的规定,在10~100 rad/s的频率范围内失配曲线可能会超出包络线的范围,会出现如图1所示的情况。

图1 0.1~100 rad/s范围内拟配结果Fig.1 The diagram in the range of 0.1 ~ 100 rad/s
由图1可以看出,在0.1~10 rad/s的频率范围内拟合精度较高,相角差与幅值差非常小;而在10~100 rad/s范围内,出现了失配曲线发散至包络线之外,这将会使得飞行品质的评价结果不准确。
若在0.1~100 rad/s的频率范围均匀地取30个点进行拟配,失配曲线将会很好地处在失配包络曲线内,拟配结果如图2所示。

图2 0.1~100 rad/s范围内拟配结果Fig.2 The diagram in the range of 0.1 ~ 100 rad/s
从图2可以看出,在0.1~100 rad/s的频率范围内失配曲线都较好地限制在失配包络曲线范围内。但是试飞经验表明[1],驾驶员对1~4 rad/s范围内的飞机动态变化最为敏感,因此,对该频段内的匹配误差最为敏感,拟配过程中失配曲线在包络线内的前提下,应尽量使该频段内的拟配误差尽可能地小。
对比图1和图2可以看出,图1在1~4 rad/s频段范围内拟配精度明显高于图2,但是在10~100 rad/s范围内却出现了失配的现象。图2在0.1~100 rad/s整个频段范围内均未出现失配现象,但是对于驾驶员最为关心的1~4 rad/s频段内失配度较高,这样可能会导致评价结果的不准确。
基于上述分析,本文提出了一种改进的带加权因子的等效系统拟配方法。
2 改进的等效系统拟配方法
2.1 基本思路
综合上述提到的两种拟配方法的优缺点,提出这样一种假想:在1~10 rad/s频段内正常进行拟配;而对于10~100 rad/s频段内的点,在拟配时乘以一个系数k0(<1),这样将会使得10~100 rad/s频段内的10个点在目标函数中的比重将会减小,而1~10 rad/s频段内的拟合精度仍然维持在一个较高的水平。
经过运算,这种假想确实能够将上述两种指标结合起来,达到很好的拟配效果,使得失配曲线能够合理地位于失配包络线范围内。
2.2 仿真分析
基于以上思路,改进后的目标函数为:

当k0取不同值时,目标函数的值以及失配参数的分布也各不相同。以B种飞行阶段,H=5 000 m,Ma=0.6为例,下面就不同的k0值对最终结果的影响进行分析。
为提高拟配精度,本文先采用遗传算法对8个参数值进行求解;然后再利用所得的值作为初值,利用最小二乘法进一步寻优以提高拟配精度。
当k0分别取0.100,0.010,0.001时,拟配计算结果如表1所示,它们各自所对应的失配包络图如图3~图5所示。

表1 不同加权系数下的低阶等效系统参数Table 1 Low order equivalent system parameters at different weight coefficients
从上述的各个拟配结果的失配包络图看,图3所示k0=0.100及k0=0.010的拟配结果较好,失配曲线在包络线内的分布有了明显改进。在驾驶员最关心的频段内拟配精度较高,并且k0=0.010的失配曲线在该频段内的波动程度要更小一些。在10~100 rad/s频段内,两者都保持了较好的分布性。对于k0=0.001的情况,虽然在1~10 rad/s频段内拟配精度很高,但在10~100 rad/s频段内失配曲线迅速发散,失配曲线的分布并不合理。
综上所述,采用带加权系数的等效拟配方法在对10~100 rad/s频段内10个点进行加权运算时,加权系数k0存在一个最优区间,在此区间内,失配曲线的分布得到了较大改进,其分布在整个频段内也显得更加合理。试分析其原因,当k0大于该区间时,后10个点的权重过高,影响了前10个点的拟配精度;当k0小于该区间时,后10个点对拟配结果的影响较小,对失配曲线的改进并不明显。基于上述 分析,k0的建议值取在[0.010,0.100]区间内。
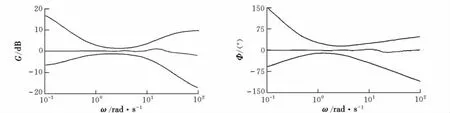
图3 k0=0.100时的失配包络图Fig.3 The mismatch envelope diagram when k0=0.100

图4 k0=0.010时的失配包络图Fig.4 The mismatch envelope diagram when k0=0.010
2.3 改进的等效拟配的总体思路
基于上述分析,本文提出的改进的等效系统拟配的具体思路如下:
(1)确定所需拟配的等效拟配模型的形式,并建立相应的带加权系数的目标函数;
(2)利用遗传算法求取使得目标函数最小的等效系统的初值;
(3)以步骤(2)所求取的等效系统的各参数值为初值,利用最小二乘法进一步优化各个参数,得到最终的等效系统。
(4)在所求得的等效系统的基础上,根据相关准则进行飞行品质的分析。
3 结论
(1)本文仅以纵向俯仰角速度与驾驶杆力的传递函数模型为例,提出了改进的等效拟配方法,对于不同的等效拟配过程,ω1,ω2的选取并不是一定的[1],但都可借鉴该方法的思路,对频率ω2外的点进行加权拟配。
(2)采用本文提出的改进的等效系统拟配方法,避免了初值的选取,且使得失配曲线不仅具有很高的拟合精度,而且失配参数在包络线内的分布显得十分合理,减少了工作量,能够快速地得到合理的等效拟配结果,适合于工程应用。
[1]高金源,李陆毅,冯亚昌,等.飞机飞行品质[M].北京:国防工业出版社,2003:60.
[2]章萌,章卫国.基于混沌差分进化算法的飞机等效系统拟配研究[J].系统仿真学报,2010,23(9):2060-2064.
[3]聂瑞,章卫国.基于改进的NSGA-Ⅱ算法的飞机等效拟配[J].西北工业大学学报,2011,29(1):27-33.
[4]杨蔷薇,张翔伦.遗传算法在等效系统拟配中的应用[J].飞行力学,2005,23(3):45-47.
[5]李大伟,徐浩军.基于等效系统拟配的人-机闭环系统稳定性研究[J].飞行力学,2011,29(4):19-22.
[6]中国国家标准化管理委员会.GJB 2874-1997 电传操纵系统飞机的飞行品质[S].北京:国防科学技术工业委员会,1997.
[7]DOD.MIL-HDBK-1797 Flying qualities of piloted aircraft[S].USA:Department of Defense,1997.
[8]孟捷,徐浩军,葛志浩.等效系统参数辨识法在飞行品质评价中的应用[J].数学的实践与认识学,2008,38(8):79-84.
