近空间飞行器滑翔再入控制的研究方法与进展

尹佳杰，都延丽，陆宇平

（南京航空航天大学航天学院，江苏南京 210016）

0 引言

21世纪以来，近空间这个特殊空域的价值受到了世界各国的高度重视，近空间飞行器（Near Space Vehicle，NSV）的研究也随之备受关注。参照工程实际应用，近空间可以分为低层（20～30 km）、中层（30 ～70 km）和远层（70 ～100 km）［1］。NSV 则兼具航空器、轨道战斗机和空天飞行器的优点，尤其是飞行速度大于Ma=5的高超声速NSV，在快速远程打击、战场信息控制和民用长途运输等方面更具备优势。鉴于高超声速NSV十分重要的军事及民用价值，世界各航空航天大国进行了相当深入的研究，著名的验证机有X-43，X-37B和HTV-2等。我国也开展了一系列基础研究和论证工作［2-4］，其中针对有动力高超声速巡航段的研究较多，但对其无动力返回段的研究尚不多见。NSV的返回过程是研制该飞行器的重点与难点，此过程可分为初期再入段、末端区域能量管理段和进场着陆段［4］。目前，现有研究集中于NSV的再入预测制导与轨迹规划问题，对其再入段飞行控制算法的研究还不够深入。故本文将考虑高超声速NSV从中远层近空间返回的初始段，对其无动力滑翔再入的飞行控制发展现状进行分析和评述。

德国科学家Saenger首次提出跳跃滑翔的概念［5］，并构想了一种有翼滑翔轰炸机从远层近空间沿大气层进行振幅衰减的跳跃式再入飞行。钱学森则提出一种火箭助推再入大气层滑翔机动飞行的高速运输系统［5-6］，该再入飞行采用几乎没有波动的平衡滑翔弹道。高超声速NSV再入时处于无动力、长时间滑翔的状态，可采用Saenger弹道或钱学森弹道形式，此过程是NSV返回过程中最恶劣、最复杂的一段。首先，空气温度和密度的大范围变动使得NSV的气动特性呈现出严重的非线性特点；其次，气动参数的不确定性、执行机构的未建模动态、外界干扰等又使其动力学模型具有很大的不确定性；另外，大空域、再入机动飞行使NSV各通道间的耦合作用更加强烈。因此，高超声速NSV的再入过程具备严重非线性、强不确定和强耦合的对象特征，这为其控制系统的设计带来了巨大挑战。具体来说，主要体现在飞行控制方式和控制算法设计两方面的困难。首先，从大气较稀薄区在短时间内进入稠密大气中，单纯依靠NSV的气动舵面将无法实现在空气稀薄区对飞行器的良好操纵与控制，因此再入的控制方式问题亟待解决。其次，NSV再入段需进行有控、无滚、有迎角高速飞行，其严重非线性、强不确定和强耦合的对象特征决定了控制算法的设计面临非线性不确定控制难题和强耦合控制的难题；同时，再入飞行还受到过程约束（动压约束、过载约束、热流约束、舵面偏转约束）、终端约束和路径约束等诸多限制，这些因素都给NSV的控制算法设计带来新的难题。

综上所述，本文将对NSV的再入飞行控制方式和控制算法研究现状进行分析，其中后者主要就非线性不确定控制问题、多约束控制问题和强耦合控制问题开展总结和分析工作。

1 NSV再入非线性模型

与传统再入飞行器和常规弹头相比，高超声速NSV的气动布局存在明显差异。前者常采用旋成体外形，气动性能较低。后者要实现再入滑翔飞行，须具备良好的气动性能，一般采用乘波构型、升力体气动布局、轴对称锥形体布局等外形。针对不同布局有不同的NSV气动参数表达，但再入力学方程的形式类似。文献［7］给出了X-38这种再入NSV的非线性方程，NSV被看作刚体且再入时作无动力滑翔飞行。文献［8］给出高超声速NSV的无动力再入姿态非线性模型，忽略了地球自转角速度和飞行器质量变化，设计NSV再入姿态控制器即基于以上模型，而轨迹控制器则在姿态控制器的基础上进行设计［9］。

2 NSV再入段飞行控制方式

初期再入段是NSV由中远层近空间返回的重要阶段，此阶段大气环境变化剧烈。在低空稠密大气层内，空气动力舵能够提供可观的气动控制力，用于改变飞行姿态与轨迹。但是在中远层近空间，大气密度迅速下降将导致气动舵面效率迅速降低，单纯依靠其作用已很难满足NSV的操控要求，故需要增加其他方式的直接控制力。因此，为保证NSV的控制能力，须采用气动舵面和其他控制形式相结合的气动复合控制方式［10］，主要包括空气动力控制与反推力控制系统［11］（Reaction Control System，RCS）以及变质心控制等方式的结合。

2.1 空气动力控制

空气动力控制指NSV依靠自身舵面的偏转产生滚转、偏航和俯仰力矩，此控制力矩能够引起机体轴角速率的变化，从而引起姿态角的变化，进而影响轨迹的运动。在滑翔再入段，NSV以较大迎角飞行，机身阻挡了方向舵上的气流，故再入初期一般不使用方向舵来控制飞行器，而用升降舵和副翼来影响俯仰和偏航力矩［7，12］。由于近空间上部空气稀薄，NSV动压较小，所以该控制方式存在效率低下和高速飞行引起的舵面烧蚀等问题。

2.2 RCS控制

在中远层近空间，空气动力不足以控制NSV，需采用RCS喷气的方式产生控制力。在再入起始段，RCS可提供直接控制力。随高度逐渐下降，空气密度变大，动压增加，舵面控制效率也逐渐提高，此时气动舵面要和RCS复合使用，但RCS具有离散工作特性，需要进行脉宽调制［11，13］。文献［7］给出了一种动压分配控制力矩的复合控制策略。当RCS向气动舵面操纵过渡时，力矩分配可由过渡函数来表达:

式中，Mthrust为RCS指令力矩；Maero为气动舵面指令力矩；Mcmd为总的指令力矩；q为飞行器动压。文献［13］针对一类再入NSV设计姿态控制系统，采用了基于Mamdani模型的模糊RCS控制器，输入为姿态角偏差和偏差速率，输出为RCS开启的喷管数目，在控制中能根据专家经验更精确地控制RCS的输出。文献［14］将RCS控制应用在NSV再入横向控制中，偏航喷气流抑制了滚转角速度的响应，从而有效地抑制了荷兰滚。RCS控制不依赖大气状况，高空效率高且响应更快，但是增加了飞行器质量而减小了载荷能力。为此要最大化飞行器的有效载荷，多采用RCS与气动舵面复合控制的方式，以避免携带过多的RCS燃料。例如，Doman［11］针对再入过程中舵面的脆弱性和舵面偏角的饱和性，采用舵面和RCS混合控制方式，并利用线性规划法进行了控制分配。

2.3 变质心控制

近年来，高超声速变质心控制作为新兴技术，逐渐引起人们的关注。该控制方式通过调整内部滑块与飞行器间的相对位置使系统质心发生变化，改变了力臂从而产生附加稳定力矩来控制姿态运动。变质心机构不会影响飞行器的气动外形，也无需考虑烧蚀问题，而且能产生很大的控制力和力矩，节省了系统的能量消耗［15］。但该控制对气动力的依赖较大，在气动力不足时需要与其他控制方式复合以实现系统响应指标，而且因受到内部空间限制，控制受限问题也比较突出。由于变质心运动特性复杂，所以关键是建立一个完整的变质心飞行器的系统动力学模型。文献［16］以再入飞行器为研究对象，研究了变质心控制，给出了影响配平迎角的三个主要因素:滑块轴向位置、横向偏移量和质量比，并指出变质心控制能力主要体现在低空段。文献［15］采用了变质心和RCS复合的控制方式，集变质心控制和RCS控制各自的优点，高空段主要使用RCS控制，低空段采用复合控制，仿真表明迎角的上升时间和超调量有较好的结果。

3 NSV再入段控制方法

高超声速滑翔再入具有飞行范围宽（高度约100～20 km）、飞行马赫数变化大（Ma=30～5）、机动性强、边界限制条件多、操纵复杂（气动舵面、RCS等的配合使用）等特点，而且再入动力学模型高度非线性，受干扰和不确定因素影响剧烈，因此要求再入段控制律具有高精度、自适应和强鲁棒特性，这对NSV控制算法的设计是一个很大的挑战。本文将从高超声速NSV再入过程存在的非线性不确定控制问题、多约束控制问题和强耦合控制问题出发，对这三方面的研究进行总结和分析。

3.1 再入段非线性不确定控制问题

针对NSV再入动力学高度非线性的特征，直接采用非线性控制策略是必然的途径。文献［17］对某再入飞行器应用了backstepping控制方法，在利用李亚谱诺夫函数保证闭环系统稳定的情况下，用递归的方法层层推导出控制变量。文献［18］将非线性动态逆方法与时标分离原则相结合，独立设计了再入段内外环回路的控制律。动态逆的优势在于它能够处理模型中的非线性，但当存在不确定因素时，系统将缺乏鲁棒性。目前应用较多的滑模控制适用于有建模误差、参数摄动和干扰的线性和非线性对象，但会引起系统的抖振，这也是该方法发展的最大障碍。文献［19］设计了基于等价控制方法的积分滑模控制器，它不要求干扰和不确定性具有已知常数界，并能够保证系统快速地趋近滑动面，实现了对NSV再入制导指令角的鲁棒解耦跟踪。文献［20］结合动态逆和滑模控制对一类再入NSV的内外环进行了控制，实现了系统的稳定性和鲁棒性，并采用饱和函数降低了滑模的抖振。

与传统飞行器相比，高超声速NSV的高度和速度跨度大，动力学特性相当复杂，故很难获得准确的数学模型。文献［21］对一类NSV设计了基于无迹卡尔曼滤波的方法，对再入过程的气动模型参数进行识别，把参数估计作为一个非线性滤波问题，降低了模型的不确定因素。鲁棒控制方法在解决参数不确定、结构不确定等方面也具有得天独厚的优势。文献［22］针对高超声速再入NSV利用μ综合方法对姿态控制律进行设计，并用遗传算法对权函数进行了优化，保证系统具有良好的鲁棒性。文献［23］设计了一种基于增益预置H∞的控制器，当存在不确定和噪声时分别对纵向和横向通道进行设计，满足了再入NSV控制系统的全局性能和鲁棒性。文献［24］对再入时的各种干扰问题，采用鲁棒模糊PID控制器，仿真验证了其可靠性和鲁棒性。但是鲁棒控制的缺点在于没有学习能力，实现时需要知道不确定的上界，这往往造成设计上的过分保守。

干扰观测器（Disturbance Observer，DO）技术简单有效，极易与非线性控制方法结合［25］。文献［26］针对X-33再入段外部扰动和不确定影响，设计了一种增益自适应滑模干扰观测器（SMDO），SMDO不需要干扰界已知，它能够在线估计出外部扰动和不确定性。文献［27］对一类NSV再入初期段采用了连续滑模控制，并设计滑模状态观测器对系统摄动和外界干扰进行估计，很好地抑制了抖振，并利用脉冲调频调宽调制器对RCS点火指令进行控制，达到了连续控制的目的。文献［28］对再入飞行器研究了一种快速模糊干扰观测器（DO），能够在线无限逼近外部干扰和不确定，弥补了传统模糊DO逼近较小误差时学习速度慢、逼近时间长的缺点，具有较好的鲁棒性和快速响应速度。但基于模糊理论的DO不足之处在于难以获取合适的模糊规则。自适应控制是解决参数不确定控制问题的另一种途径，对于再入不确定问题，它是一种很好的控制方法。文献［29］针对再入段模型的不确定性，设计了一种神经网络自适应鲁棒控制器来跟踪不确定系统的控制指令。文献［30］对一类再入NSV提出了自适应并联前馈补偿的控制方法，采用了PD反馈控制器作为前馈补偿器，旨在跟踪参考模型的输出，并采用了灵敏度分析来比较有无并联前馈系统的鲁棒性。文献［31］研究了基于RBF神经网络的自适应快速终端滑模控制和基于T-S模糊模型的自适应时变终端滑模控制两种控制器，设计了全滑模态终端滑模控制，并引入自适应控制使再入NSV能适应强干扰等的影响，但T-S模糊模型在当模型参数变化较大时会导致控制器性能下降或失效。文献［32］针对再入飞行过程中存在的复杂气动环境和不确定影响，提出了一种基于自适应二阶终端滑模的控制方案，它不需要内外扰的先验知识，通过在线自适应辨识扰动上界以消除其影响，与传统终端滑模相比，能克服气动参数摄动带来的不良影响。

3.2 再入多约束问题

高超声速NSV的再入段受到物理结构、热防护、滑翔条件等过程约束、终端约束与路径约束的限制，其中过程约束主要包括舵面约束和以下三方面约束:

（1）过载约束

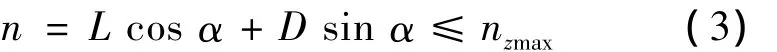
式中，nzmax为法向过载约束。

（2）动压约束

式中，qmax为最大动压。

（3）热流约束

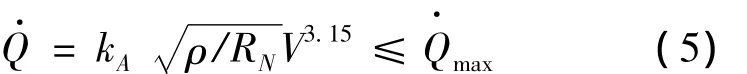
式中，kA为常数；RN为驻点曲率半径。

这些约束条件对再入轨迹规划、制导律以及控制算法设计提出了很高的要求，只有满足了这些条件，NSV才能适应再入过程的热力学环境［33］，从而保证飞行安全。文献［8］为克服输入和状态约束问题，针对再入NSV提出了SDRE（State Dependent Ricatti Equation）解耦控制器，利用无限时间性能指标求解Riccati方程，设计出最优控制律，但控制器非常复杂，加权参数调整难度大，计算量大，难以在线应用。目前，模型预测控制（Model Predictive Control，MPC）是显式处理状态和控制约束的有效方法之一，它具有滚动优化、在线反馈校正、模型预测三大特点。针对SDRE的缺点，文献［34］在此基础上采用了MPC方法，对于慢回路而言，要求跟踪性能要好；而对于快回路而言，控制量要大一些，所以要合适选择加权矩阵的大小。与SDRE相比，MPC能够进一步解决再入约束问题，不用重复设计加权项，用滚动时域优化来提高系统的鲁棒性，大大减小了计算量。文献［7，35］针对X-38再入模型，将MPC和反馈线性化结合，利用MPC将非线性模型线性离散化，把各约束条件（系统约束、推进器的推力约束、舵面偏转角约束、姿态角约束）综合起来作为输入约束，虽然通过非线性变换将模型转化为线性模型，但约束控制是非线性的，处理比较复杂。文献［36］提出了一种基于线性矩阵不等式（LMI）约束优化的再入飞行器预测控制，利用SDRE中的伪线性化模型对再入飞行器的纵向运动方程进行直接建模，保证点点可控，并简化了模型。利用LMI约束凸优化求解有约束的问题，具有很好的鲁棒性，在线求解效率高。文献［37］在高超声速NSV再入段制导中，采用了连续非线性时变预测控制，避免了复杂的数值计算。文献［38］在文献［37］的基础上，提出了基于奇异摄动理论的内外环解耦控制系统。外环耦合性较弱，在满足角速度约束的条件下，采用非线性时变预测控制实现角度跟踪；内环耦合性较强，采用了动态逆跟踪角速度指令。在处理NSV再入段输入和状态约束问题上，预测控制明显优于动态逆控制。

3.3 耦合问题

为了保证再入NSV在剧烈变化环境下的控制能力，复合控制方式取代了传统单一的控制方式，多个参与飞行器控制的执行机构间的操纵耦合加剧了系统的耦合［39］。飞行器在采用变质心方式纵侧向机动时会对滚转通道产生耦合作用，从而会使滚转角发散。而在NSV的再入过程中，各通道之间也存在着强耦合效应。

高超声速NSV的再入段要求侧滑角保持在零值附近，所以得到简化模型的纵向通道可以独立于其他通道，不存在与其他通道的耦合影响，而偏航通道和滚转通道严重耦合，并且受俯仰通道的耦合影响。高超声速NSV的飞行特性不具备小扰动线性化的假设条件，所以不能简单地采用传统的纵向、横向解耦控制来设计飞行控制系统。文献［40］建立了高超声速飞行器再入六自由度模型，可以看出该模型是一个高度非线性、强耦合及参数时变的多变量系统，同时分析了飞行器在最大升阻比下飞行时气动力对姿态角通道之间的耦合特性以及舵机对弹道的耦合特性，仿真表明，气动力参数与姿态的交叉耦合不能忽略。文献［20］为飞行器再入段设计了滑模控制器，并简化了飞行器的再入模型，在进入滑模运动后，系统的各姿态间不存在耦合作用，也就是实现滑模控制的同时也实现了各通道之间的解耦。文献［41］针对飞行器再入过程中通道间强烈的耦合效应，提出了一种最优空间转动矢量概念，对内外回路进行设计，外环回路使飞行器按最优空间转动矢量转动来跟踪姿态角并输出期望角速度，再根据姿态动力学设计内环，使内环姿态控制器跟踪期望角速度矢量，输出期望力矩，这种单通道控制器解决了普通三通道姿态耦合的问题。因此，如何消除通道间耦合效应的不良影响，达到NSV各通道运动的协调控制是急需解决的关键问题。

4 总结与展望

本文针对高超声速NSV的滑翔再入过程，分别从控制方式和控制算法两方面进行了综述。通过对其飞行特征的详细分析，总结出NSV再入控制主要存在着复合控制方式的设计、非线性不确定、多约束以及强耦合的控制难题。国内外研究现状表明，气动舵面结合RCS等方式的气动复合控制方式是NSV再入控制的必要手段。对于非线性不确定问题，目前研究较为成熟，已形成了非线性控制方法结合智能自适应及鲁棒控制方法的有效途径。而NSV再入多约束控制问题的一种解决方式，即以约束预测控制为基础的控制器设计，但如何在满足NSV多种约束及保证全局稳定性的条件下，快速有效地获得最优控制解是NSV再入控制无法回避的重要课题。此外，NSV再入过程中气动力参数与飞行状态交叉耦合的自适应控制以及多个通道耦合的协调控制研究也是未来重要的研究方向。总之，以上问题的解决关系着NSV再入控制的稳定性、机动性和控制精度，亟需吸收新方法与新技术继续开展系统深入的研究。

［1］崔尔杰.近空间飞行器研究发展现状及关键技术问题［J］.力学进展，2009，39（6）:658-673.

［2］Li X D，Xian B，Diao C，et al.Output feedback control of hypersonic vehicles based on neural network and high gain observer［J］.Science China Information Sciences，2011，54（3）:429-447.

［3］Du Y L，Wu Q X，Jiang C S，et al.Adaptive recurrentfunctional-link-network control for hypersonic vehicles with atmospheric disturbances［J］.Science China Information Sciences，2011，54（3）:482-497.

［4］吴了泥.可重复使用运载器亚轨道再入段制导与控制技术研究［D］.南京:南京航空航天大学，2009.

［5］陈小庆.高超声速滑翔飞行器机动技术研究［D］.长沙:国防科学技术大学，2011.

［6］朱凯.滑翔导弹再入制导与控制方法研究［D］.哈尔滨:哈尔滨工业大学，2011.

［7］Recasens J J，Chu Q P，Mulder J A.Robust model predictive control of a feedback linearized system for a lifting body reentry vehicle［R］.San Francisco:AIAA Guidance，Navigation，and Control Conference and Exhibit，2005.

［8］张军，毕贞法，邵晓巍.一种高超声速飞行器的非线性再入姿态控制方法［J］.空间控制技术与应用，2008，34（4）:51-54.

［9］都延丽.近空间飞行器姿态与轨迹的非线性自适应控制研究［D］.南京:南京航空航天大学，2010.

［10］Beresh S，Heineck J，Wallker S，et al.Stereoscopic PIV for jet/fin interaction measurements on a full-scale flight vehicle configuration［R］.Reno:43rd AIAA Aerospace Sciences Meeting and Exhibit，2005.

［11］Doman D，Gamble B，Ngo A.Control allocation of reaction control jets and aerodynamic surfaces for entry vehicles［R］.Hilton Head:AIAA Guidance，Navigation，and Control Conference and Exhibit，2007.

［12］宁国栋，张曙光，方振平.跨大气层飞行器再入段RCS控制特性［J］.飞行力学，2005，23（3）:16-20.

［13］黎科峰，宋剑爽，任章.基于模糊逻辑的再入RCS控制方法［J］.北京航空航天大学学报，2008，34（12）:1407-1410.

［14］Wu L N，Huang Y M，He C L.Lateral-direction control via reaction control system ［C］//International Asia Conference on.USA:IEEE，2009:52-56.

［15］王霄婷，周军，林鹏.基于变质心/RCS复合方式的再入飞行器控制系统设计方法研究［J］.航天控制，2011，29（4）:37-42.

［16］李瑞康，高长生，荆武兴.飞行器变质心控制及性能分析［J］.宇航学报，2010，31（9）:2165-2171.

［17］Lian B，Bang H，Hurtado J E.Adaptive backstepping control based autopilot design for reentry vehicle［R］.Providence:AIAA Guidance，Navigation，and Control Conference and Exhibit，2004.

［18］谭政，李新国.基于非线性动态逆的SRLV再入段控制律设计［J］.飞行力学，2009，27（3）:66-70.

［19］杨俊春，胡军，吕孝乐.高超声速飞行器再入段滑模跟踪控制设计［C］//程代展，吴敏.第26届中国控制会议.北京:北京航空航天大学出版社，2007:2-5.

［20］Wang P，Liu L H，Wu J，et al.Reentry vehicle modeling and sliding mode controller design［C］//2011 5th International Conference on Recent Advances in Space Technologies.USA:IEEE，2011:227-231.

［21］Vitale A，Corraro F，Bernard M，et al.Unscented Kalman filtering for reentry vehicle identification in the transonic regime［J］.Journal of Aircraft，2009，46（5）:1649-1659.

［22］晁涛，王松艳，杨明.基于遗传算法的高速再入飞行器μ综合控制器设计［J］.航天控制，2011，29（4）:32-36.

［23］Marcos A.A gain scheduledH-infinity controller for a reentry benchmark［R］.Toronto:AIAA Guidance，Navigation，and Control Conference，2010.

［24］Min C O，Lee D W，Cho K R，et al.Control of approach and landing phase for reentry vehicle using fuzzy logic［J］.Aerospace Science and Technology，2011，15（4）:269-282.

［25］Kim K S，Rew K H，Kim S.Disturbance observer for estimating higher order disturbances in time series expansion［J］.Automatic Control，2010，55（8）:1905-1911.

［26］Hall C，Shtessel Y.Sliding mode disturbance observerbased control for a reusable launch vehicle［R］.San Francisco:AIAA Guidance，Navigation，and Control Conference and Exhibit，2005.

［27］宁国栋，张曙光.RLV再入初期连续滑模姿态控制律设计及仿真［J］.系统仿真学报，2007，19（22）:5272-5276.

［28］黄国勇，姜长生，王玉惠.基于快速模糊干扰观测的UASV 再入 Terminal滑模控制［J］.宇航学报，2007，28（2）:292-297.

［29］Mathavaraj S，Halbe O，Padhi R.Robust control of a reusable launch vehicle in reentry phase using model following neuro-adaptive design ［R］.Toronto:AIAA Guidance，Navigation，and Control Conference，2010.

［30］Mooij E B.Parallel feedforward compensation in simple adaptive control for a winged re-entry vehicle［R］.Hilton Head:AIAA Guidance，Navigation，and Control Conference，2007.

［31］黄国勇.基于Terminal滑模的空天飞行器再入鲁棒自适应控制［D］.南京:南京航空航天大学，2007.

［32］范金锁，张合新，张明宽.基于自适应二阶终端滑模的飞行器再入姿态控制［J］.控制与决策，2012，27（3）:403-407.

［33］Pezzella G.Hypersonic environment assessment of the CIRA FTB-X reentry vehicle［J］.Aerospace Science and Technology，2012，16（1）:1-13.

［34］邵晓巍，张军，牛云涛.高超飞行器的非线性预测姿态控制［J］.弹道学报，2009，21（4）:42-46.

［35］Van W R.Combined feedback linearization and constrained model predictive control for entry flight［J］.Journal of Guidance，Control，and Dynamics，2006，29（2）:427-434.

［36］张军，梁建国，邵晓巍.基于LMI约束优化的再入飞行器预测控制［J］.动力学与控制学报，2008，6（4）:372-376.

［37］Brinda V，Dasgupta S.Guidance law for an air-breathing launch vehicle using predictive control concept［J］.Journal of Guidance，Control，and Dynamics，2006，29（6）:1460-1463.

［38］张军，王玫.一种高超声速飞行器的再入约束非线性控制方法［J］.空间控制技术与应用，2011，37（3）:35-40.

［39］Zhou F Q，He G Y，Zhou J，et al.Coupling analysis and robust controller design based on direct force/aerodynamic controlled reentry aircraft［J］.Fire Control and Command Control，2010，35（7）:66-69.

［40］齐乃明，周启航，秦昌茂.高超声速飞行器六自由度建模及耦合特性分析［J］.弹箭与制导学报，2012，32（1）:49-52.

［41］王志刚，宁宇.基于最优空间转动矢量的升力式再入飞行器单通道姿态控制器设计［J］.科学技术与工程，2012，12（6）:1325-1328.