含参数及绝对值的二次函数解题策略初探

☉江苏省无锡高等师范学校 张 超

高中数学以函数为主线，而二次函数作为中学阶段函数的典型代表，其应用十分广泛.纵观近十年高考题，有关含参数及绝对值的二次函数综合性试题，由于呈现出命题立意新颖、综合性强、解题难度大等特点，更是成为了高考命题的新热点，且往往以压轴题的形式出现，学生解答较困难.引导学生对高三复习经典题型进行探究与解题思想归类，有助于开拓学生思维，培养学生思维品质和创新能力.为此，我们首先对此类含参数及绝对值的二次函数图像和性质进行梳理，并对此类题型的常用求解策略进行例析，供参考.

一、知识梳理

即绝对值函数可以转化成分段函数，对于分段函数给定自变量求函数值时，应根据自变量的范围，利用相应的解析式直接求解；若给定函数值求自变量，应根据函数每一段的解析式分别求解，但应注意检验该值是否在相应的自变量取值范围之内；若其中含有参数，要对参数的范围进行讨论.

二、策略探究

策略1：“以形助数”为主，“以数定形”为辅

例1 （2010·全国卷Ⅰ）直线y=1与曲线有4个交点，则实数a的取值范围是________.

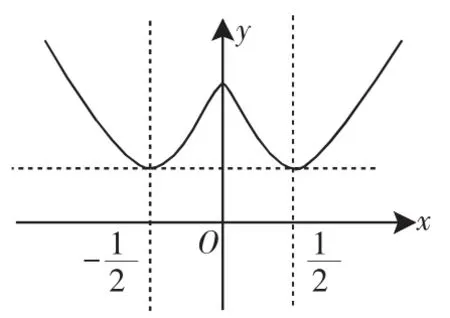
图1

点评：本题体现了数形结合的思想，它常用来研究方程根的情况、讨论函数的值域（最值）及求变量的取值范围等，对这类内容的选择题、填空题，数形结合特别有效.从历年的高考题来看，数形结合的重点是研究 “以形助数”，但“以数定形”也不容忽视.

策略2：运用思想方法灵活转化试题

以绝对值函数为载体，运用函数、方程及不等式的思想，借助三者之间的依赖关系，灵活转化，解决运动和变化中出现的问题，能给学生提供思考的空间，使他们的聪明才智在解题中得到充分的展示，进而体现了高考数学考素质，考能力的要求.

例2（2009年扬大附中高三调研卷）若函数f（x）=图像上存在点P（x1，f（x1））对任意a∈（－1，3］都不在x轴上方，求b的最小值.

解析：由已知，对任意a∈（－1，3］，存在x有f（x）≤0，即可令，h（x）=－x2+b，函数g（x）与h（x）的图像如图2，当a=3或－1时，有g1（x）=.比较函数g（x）与h（x）的图像位置可以发现，当抛物线h（x）与射线g（x）=x+3相切时，b有最小值.故由，消去y有x2+x+3－b=0，由Δ=0解得b=故b的最小值为

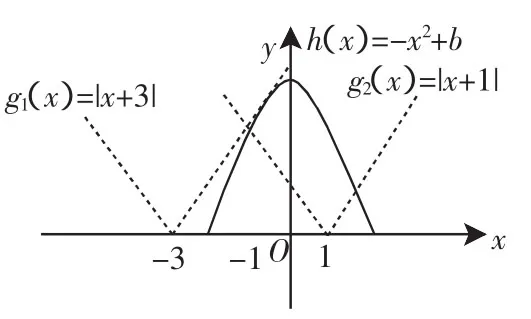
图2

点评：本题将已知条件转化为∀a∈（－1，3］，∃x有f（x）≤0，进而转化为g（x）≤h（x），通过比较g（x）与h（x）的图像的位置找到解题途径.解答关键是由条件和图像确定a和b的取值范围，去掉绝对值符号得到a与b的关系式，再消元转化为复合函数求值域.

策略3：实施“分类讨论”，分层解决问题

当所研究的问题含有参数时，往往要对参数进行讨论.分类时注意要全面，本着“不重复，不遗漏”的原则进行，最后要有概括性的总结，叙述时力争做到条理简洁，语言精练.

例3（2009年上海市卢湾区高考一模）设函数f（x）=，常数a为实数）.

（1）若f（x）为偶函数，求实数a的值；

（2）设a＞2，求函数f（x）的最小值.

解析：（1）a=0（略）.

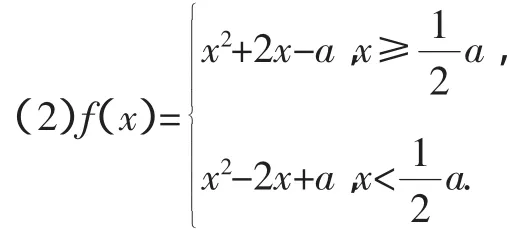
点评：本题第二问首先要根据绝对值的意义，将所给函数化为熟知的分段函数，然后结合a的取值范围和每一段的一元二次函数的单调性求出每一段的最小值，最后只需比较两最小值的大小，取较小的即可.

总之，在求解含参数及绝对值的二次函数问题中，让学生充分重视绝对值函数的类型及其转化方法是解题的关键，掌握二次函数的图像和性质，并充分重视数型结合思想是突破难点的重要手段.

1.孙福明.二次函数压轴题的解题策略［J］.数学通讯，2003（15）.

2.于亦香.对一道函数绝对值问题的探究［J］.中学数学，2012（7）. ■