多角度证明不等式一例

☉山东省东营市第一中学 王凤霞 杨兴贺

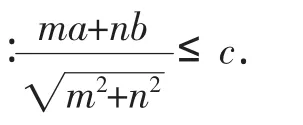
方法一（综合法）

证明：因为a，b为直角三角形的两直角边的长，c为斜边的长，所以a2+b2=c2.

又（mb－na）2≥0，即m2b2－2mnab+n2a2≥0，

所以m2（c2－a2）－2mnab+n2（c2－b2）≥0，

c2（m2+n2）≥m2a2+2mnab+n2b2，

即c2（m2+n2）≥（ma+nb）2.

而c>0，ma+nb>0，所以

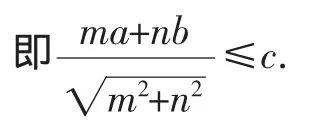
由于比较法和分析法相对于综合法较简单，此处略.

方法二（构造函数法）

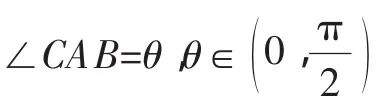
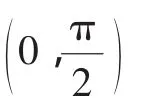
方法三（三角换元法）

方法四（向量法）

证明：设a=（a，b），b=（m，n）.由题意知而cos〈a，b〉，所以，即ma+nb≤，所以

方法五（数形结合法）

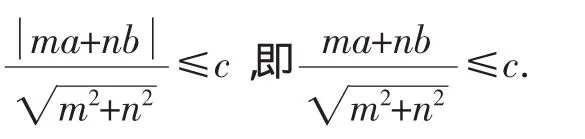
以上我们是从不同的角度和侧面，找出问题的本质，探求知识的相互关系，来解决问题，从而扩展了学生的思维空间，丰富学生的解题思路.■