高考文科“概率统计”解答题将“何去何从”

☉湖北省黄石市第一中学 杨瑞强 秦 菊

2012年高考早已落下帷幕，纵观新课改省份的“概率统计”部分的解答题，虽然试题难度不大，但是绝大多数亮点纷呈，让人耳聪目明、眼前一亮.将统计与概率问题水乳交融——你中有我，我中有你，是她们的共同亮点.下面摘录部分高考（或模拟）试题加以赏析，以期对2013年的备考复习有所帮助.

一、借助频率分布直方图，考查独立性检验与古典概型

例1（2012年辽宁高考文科卷）电视传媒公司为了了解某地区电视观众对某体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图，如图1.

将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.

（I）根据已知条件完成下面2×2列联表，并据此资料你是否认为“体育迷”与性别有关？

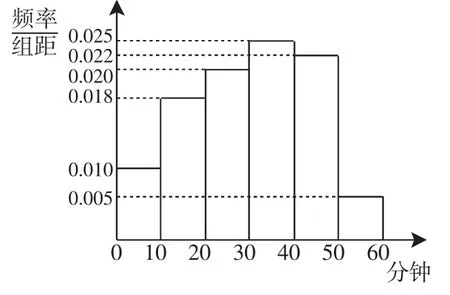
图1

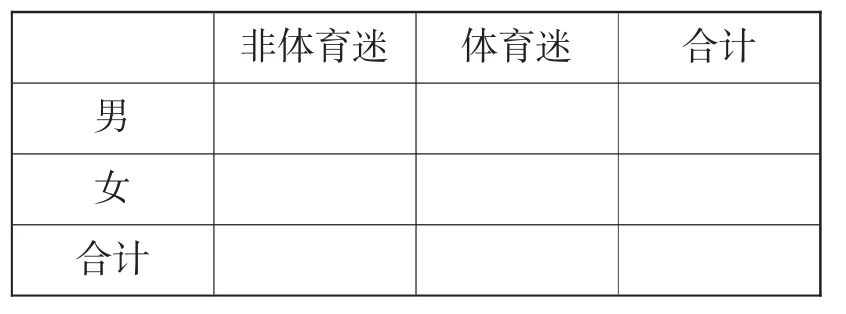
（II）将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.

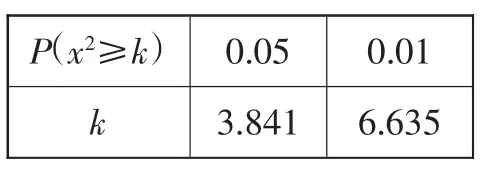
解：（I）由频率分布直方图可知，在抽取的100人中，“体育迷”有25人，从而2×2列联表如下：

将2×2列联表中的数据代入公式计算，得

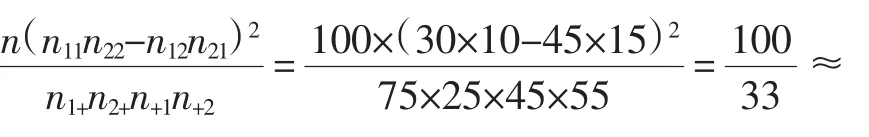
因为3.030＜3.841，所以没有理由认为“体育迷”与性别有关.

（II）由频率分布直方图知，“超级体育迷”为5人，从而一切可能结果所组成的基本事件空间为：

Ω=（a1，a2），（a1，a3），（a2，a3），（a1，b1），（a1，b2），（a2，b1），（a2，b2），（a3，b1），（a3，b2），（b1，b2）

其中ai表示男性，i=1，2，3，bj表示男性，j=1，2.Ω由10个基本事件组成，而且这些基本事件的出现是等可能的.

评析：本题借助统计中的频率分布直方图，考查独立性检验与古典概型.准确读取频率分布直方图中的数据是解题的关键.

二、借助频率分布直方图（或分布表），考查基本统计量——平均数、中位数、众数

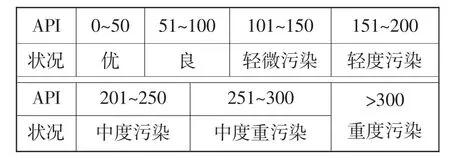
例2（2012年湖北省七市联考文科卷）城市的空气质量以其空气质量指数API（为整数）衡量，指数越大，级别越高，说明污染越严重，对人体健康的影响也越明显.根据API的不同，可将空气质量分级如下表：

为了解某城市2011年的空气质量情况，现从该城市一年空气质量指数API的监测数据库中，用简单随机抽样方法抽取30个空气质量指数API进行分析，得到如下数据：

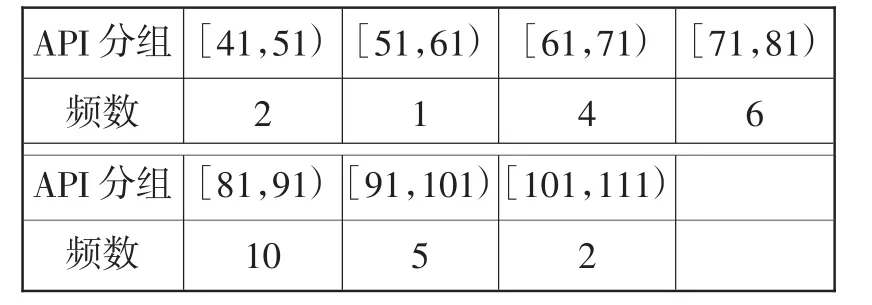
（I）在答题卡上完成频率分布直方图；

（II）根据频率分布直方图，估计质量指数API的中位数与平均数；

（III）估计该城市一年中空气质量为优与良的概率.

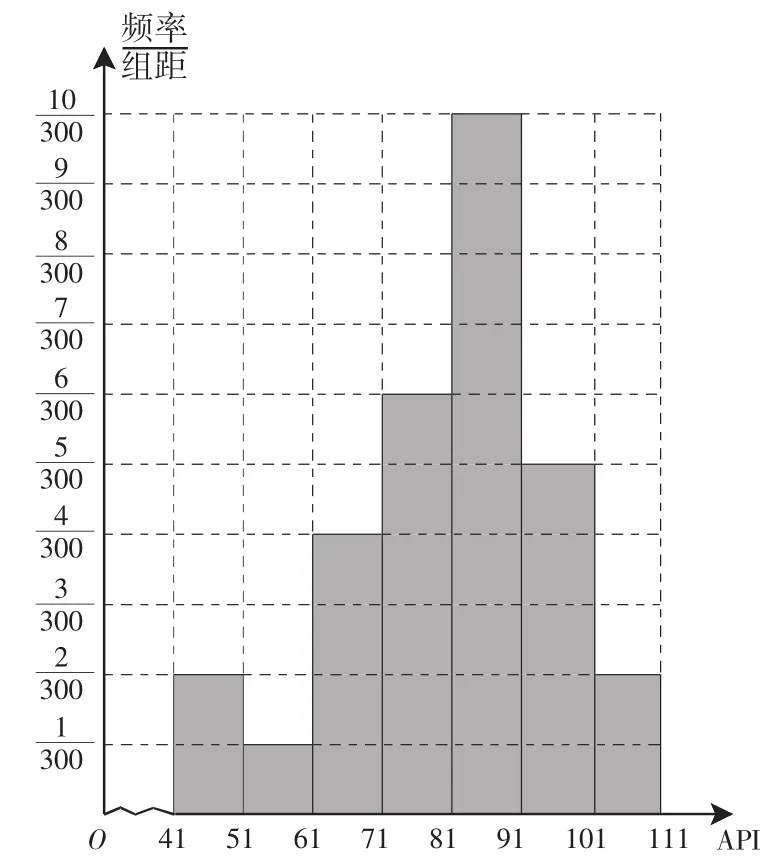
图2

解：（Ⅰ）频率分布直方图如图2所示.（Ⅱ）设质量指数API的中位数为x，则

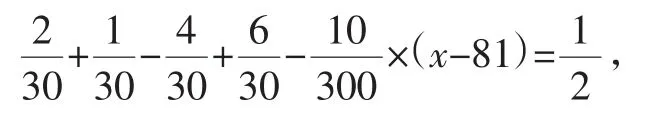
解得x=83.

评析：本题主要让学生根据统计图表，完善其相应的频率分布直方图，并借助频率分布直方图估计统计基本量——中位数与平均数，同时根据统计频率推测概率.

三、借助回归直线知识的载体，考查函数最值

例3（2012年福建高考文科卷）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：

（I）求回归直线方程ˆ=bx+a，其中b=-20

（II）预计在今后的销售中，销量与单价仍然服从（I）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）

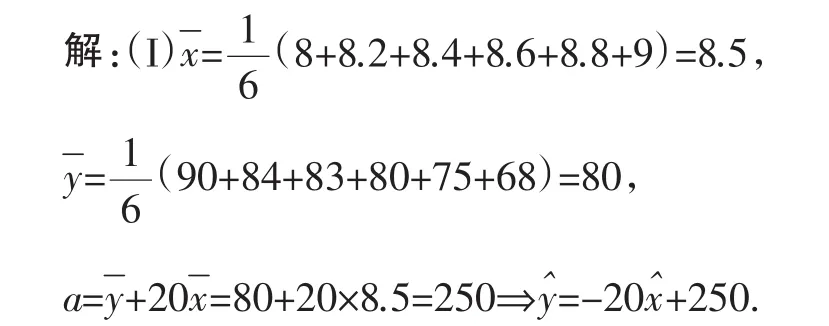
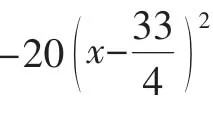
所以该产品的单价应定为8.25元时，工厂获得的利润最大.

评析：本题主要让学生根据统计图表中的数据，求出回归直线方程，并在此基础上建立函数模型（“利润与销量”的二次函数），转化为探求函数最值问题.

四、借助表格数据探究回归方程，考查变量间的相关关系

例4（2012年湖北省八市联考文科卷）某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料：

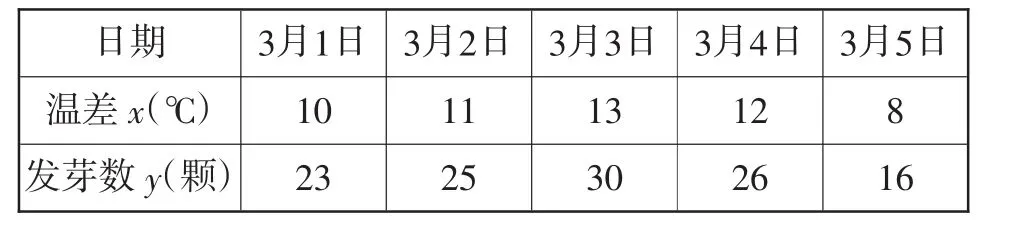
（Ⅰ）从3月1日至3月5日中任选2天，记发芽的种子数分别为m，n，求事件“m，n均小于25”的概率；

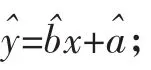
（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（Ⅱ）所得的线性回归方程是否可靠.

解：（Ⅰ）m，n构成的基本事件（m，n） 有：（23，25），（23，30），（23，26），（23，16），（25，30），（25，26），（25，16），（30，26），（30，16），（26，16），共有10个.

当x=8时，y=17.

与检验数据的误差均为1，满足题意.故认为得到的线性回归方程是可靠的.

评析：本题主要让学生根据统计图表中的数据，建立线性回归直线方程，并根据误差范围推测检验线性回归方程的可靠性.

在新课程背景下，文科数学取消了计数原理与排列组合等知识，古典概型中计数主要是通过列举法来完成，方法单一化，操作机械化.因此，概率知识部分的考查难度降低.但是，新课程文科高考开创了将统计与概率巧妙结合的新局面.将统计中的统计图（茎叶图、频率分布表、频率分布直方图等）、数字特征（平均数、中位数、众数、标准差等）、抽样方法（简单随机抽样、分层抽样、系统抽样等）、回归分析、独立性检验等统计知识与古典概率的巧妙穿插，在考查统计知识的同时有效地考查了概率知识，打破了以前统计考小题，概率考大题的陈旧局面.我们深信这样的题型布局，在今后的新课程文科高考必将延续.