解释线性回归问题的新视角——向量法

☉广东省中山纪念中学 徐全德

在普通高中新课标教材人教A版必修3和选修（理科2-3，文科1-2）分两部分介绍了统计中的线性回归知识，此部分内容的教学难点是公式推导过程繁杂、数据运算量大，不易理解和掌握.本文将尝试从向量的视角，利用向量的基本运算来证明和解释线性回归中的几个问题，供各位教师教学时参考.

一、从向量的角度看回归系数的推导

1.利用平面向量数量积的几何意义推导回归系数

对于一组具有线性相关关系的数据（x1，y1），（x2，y2），…，（xn，yn），如图：

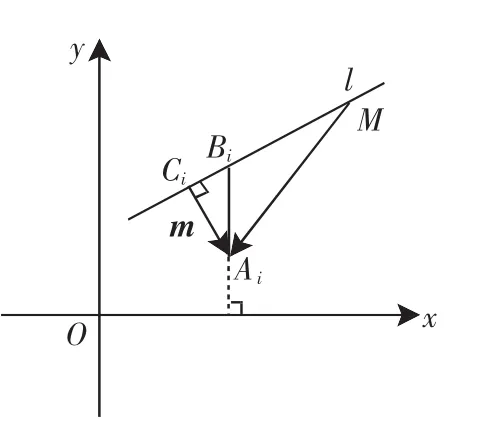
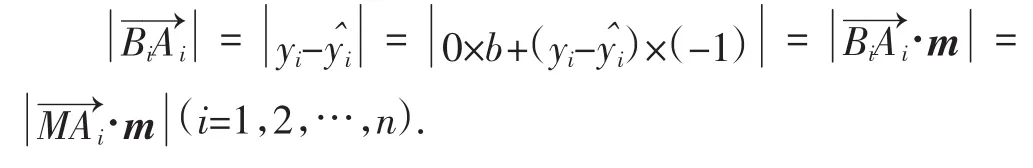
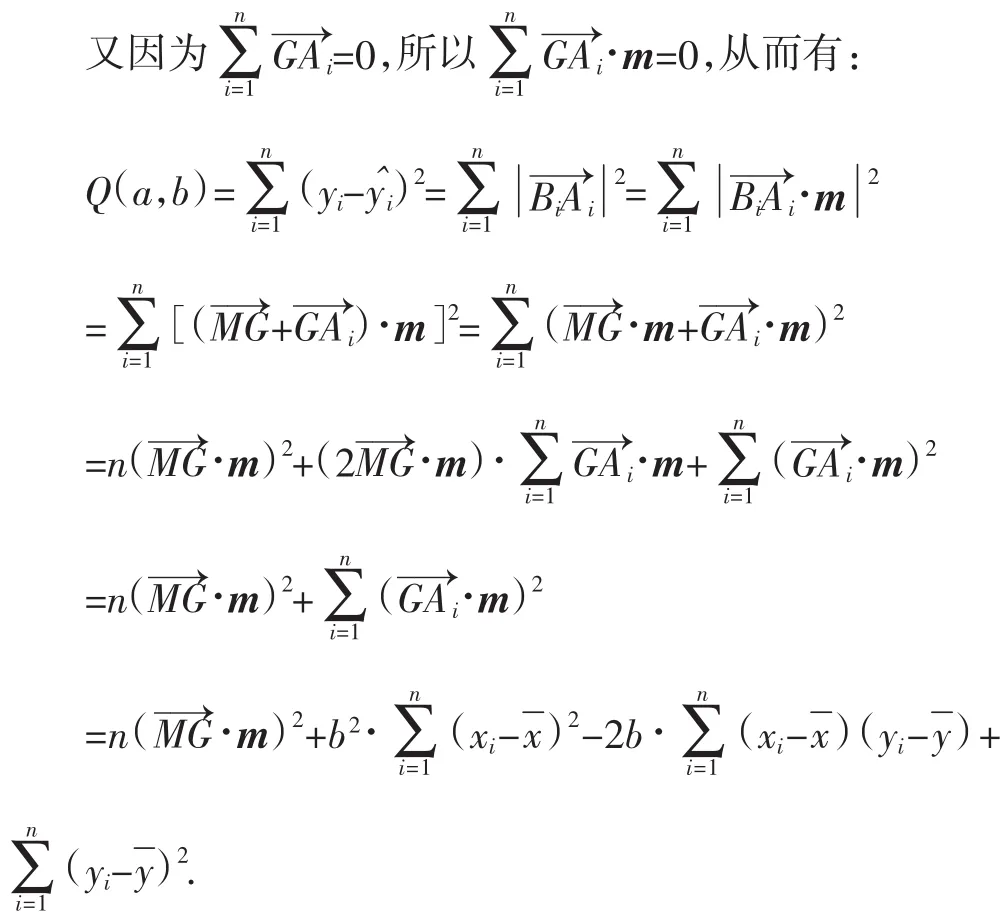
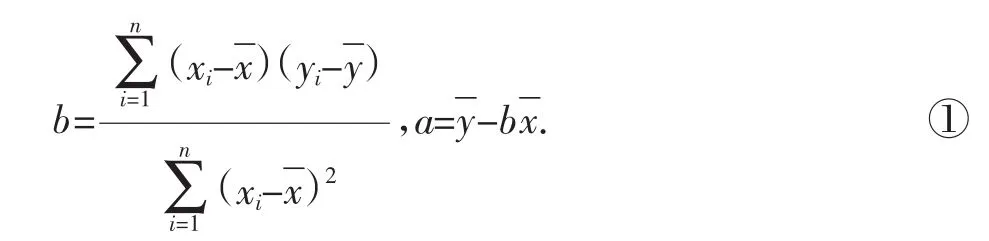
2.利用向量的数量积的代数运算推导回归系数

为了叙述问题的方便，本文引进四个n维向量：

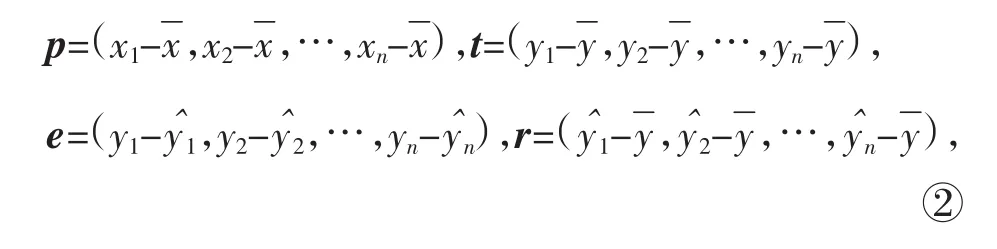
下面就来介绍回归系数的另一种推导方法：

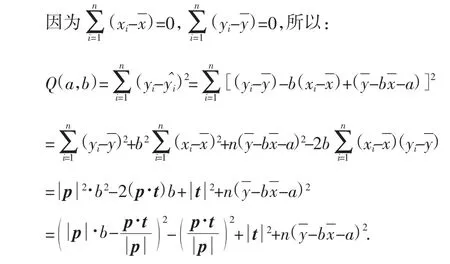
说明：由向量的数量积知，公式①和公式③是一样的，但向量表示在形式上会更简单、运算上更方便，这也是用向量法来描述统计问题的“优势”所在.

二、从向量的角度分析相关系数的意义

设向量p与t的夹角为θ，则相关系数：

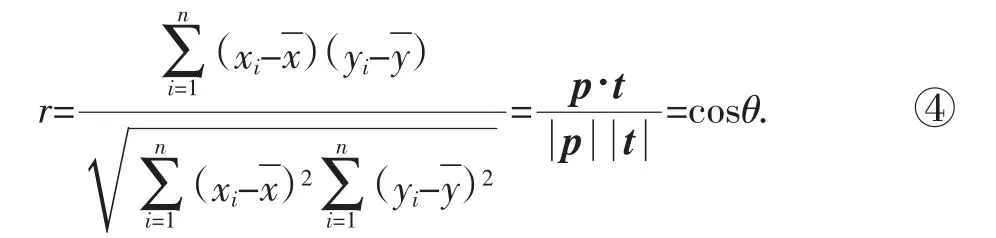
利用公式④可以这样解释相关系数r的意义：当越大，且时，θ→0或π，从而向量p与t越接近于共线.不妨设t≈bp（b为实常数），则：

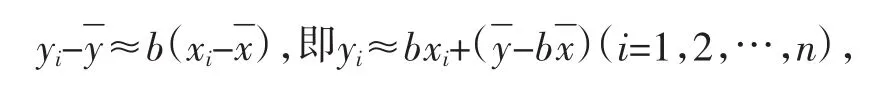
这表明这组数据的线性相关性越强.

反之，当这组数据的线性相关性越强，则由上述过程易知：越大，且

三、从向量的角度解释回归模型中相关指数的意义

1.从偏差平方和分解的角度解释相关指数的意义

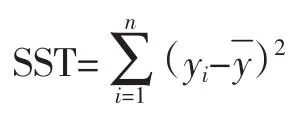
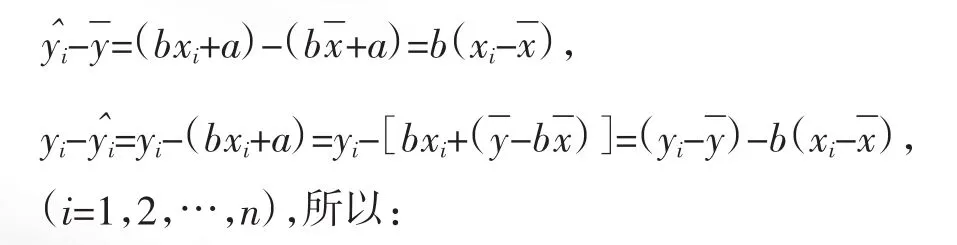
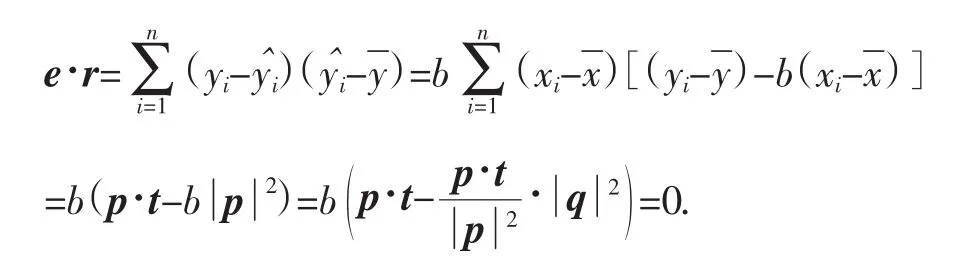
由公式⑤知：在线性回归模型中，相关指数：

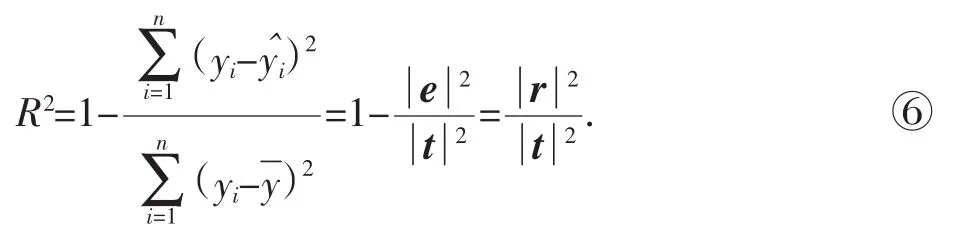
即相关指数等于回归平方和与总偏差平方和的商.因此，相关指数R2表示解释变量对于预报变量的贡献率：R2越大，表示回归的效果越好.

2.从相关系数和相关指数关系的角度解释相关指数的意义

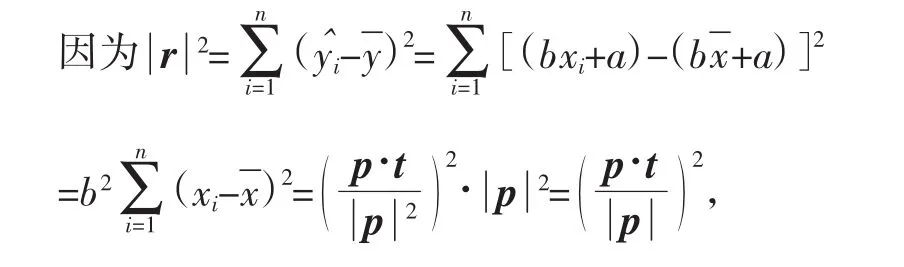
由此及公式⑥得相关指数：

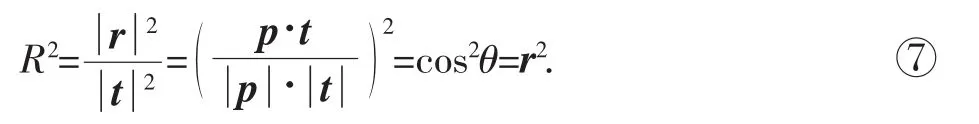
即相关指数等于相关系数的平方.

因此，在一元线性回归模型中，相关指数R2和相关系数r都能刻画线性回归模型拟合数据的效果：r越大，R2就越大，表示解释变量和预报变量的线性相关性越强，模型拟合数据的效果就越好.

由上述过程可以看到：用向量的方法推导线性回归问题中的相关公式，显得更加方便、简捷，再次体现了向量法的神奇之效，希望对各位教师教学这部分内容时有一定的帮助.