分数指数和数学符号教学的标本意义——《分数指数幂》教学设计与评注

☉河南省许昌市普通教育教学研究室 张 蕴

前不久笔者有幸参加我市“名师”的评选活动，其中评课环节的课题为必修一《分数指数幂》.初看这节内容似乎很浅显，只是初中知识的简单延伸，但细细品味，始觉其意蕴丰厚.她简直就是一部数学符号史的缩影，不仅展示了数学符号的简洁与美观，而且体现了数学符号创立的艰辛与曲折、数学“规定”的合理与兼容，处处闪烁着人类文明的智慧之光.从这个角度讲，分数指数是数学符号的标本，探究此类课型的设计与教学具有标本意义.

鉴于以上理解，笔者以数学符号史为背景，以指数范围的扩充为主线，以“规定”的合理性为点缀，设计了一堂别开生面的数学文化课.现将该教学设计整理成文，供大家探讨.

一、初中知识回顾

初中我们学习了an，其中a称为底数，n称为指数，an的结果称为幂（冪）.请问同学们知道幂的含义吗？

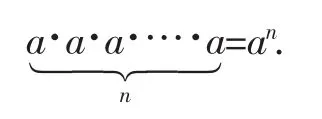
这一简洁明快的符号从1484年至1637年，前后花了153年，最终由笛卡儿创立，并不断深化.

评注：（1）在无疑处质疑，一石激起千层浪，旨在提高学生的兴趣.

“幂”的解释，加深了学生对符号an的理解，可谓古今互通，中西合璧，为学生讲述了一个富有情趣的数学故事.另外著名演员杨幂姓名的解释也令学生情绪高涨.（据说杨幂的母亲也姓杨，一家三口都姓杨，即杨的三次方，故名杨幂）

（2）让学生关注这一数学符号，感受她的简洁，理解她的内涵，了解她的历史，期待她的发展.

二、新课探究

1.根式

an运算的几种形式：

（1）计算34的值；（2）解方程：x2=2；（3）解方程：2x=3.

评注：an运算的形式主要有三种，从整体上把握知识的结构.

以下研究（2）：

解下列方程：x2=2、x2=0、x2=-2；x4=2、x4=0、x4=-2.

解下列方程：x3=3、x3=0、x3=-3；x5=3、x5=0、x5=-3.

解方程：xn=a（n＞1，n∈N*）.

一般地，如果一个实数x满足xn=a（n＞1，n∈N*），那么称x为a的n次实数方根.

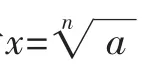
规定：0的n次实数方根等于0.

评注：（1）由特殊到一般，利用类比的方式将二次根式、三次根式推广至n次实数方根.

（2）以解方程的形式让学生理解a的约束条件、n分奇偶性讨论的必要性！

（3）初步体会“规定”的合理性.

例1求下列各式的值：

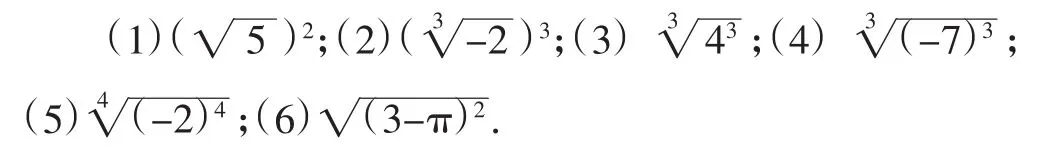
评注：（1）概括两个重要结论：

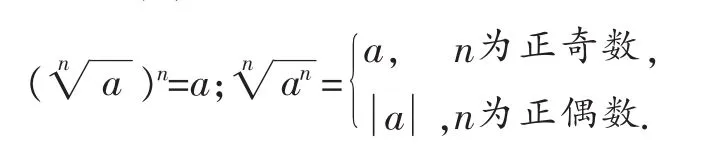
（2）适当改编和组织教材例题，使选题更具典型性，为学生概括一般结论做好应有的铺垫.

2.分数指数幂

初中学习了正整数指数幂，易知运算法则为如下四条：

am·an=am+n；am÷an=am-n；（am）n=amn；（ab）m=ambm.

其中m，n∈N*，m＞n，a＞0，b＞0.

规定：a0=1（a≠0）.

问题1：这一规定合理吗？为什么一定要a≠0这一限制？

问题2：你会解释a-2的含义吗？

规定：a-n=（a≠0，n∈N*）.

至此，实现了正整数指数幂向整数指数幂的扩充，运算法则也从四条精简为三条，即：

am·an=am+n；（am）n=amn；（ab）m=ambm.

其中m，n∈Z，a＞0，b＞0.

评注：（1）在一个司空见惯的“规定”处设问，大大出乎学生的意料，而恰恰这一看似不经意的设问，为负整数指数幂的出场准备了必要的条件.并让学生进一步体会“规定”的合理性和兼容性.

（2）对运算法则的精简体现了思维的简约性，其中隐隐透着公理化思想.

问题3：你会合理规定的含义吗？呢？呢？

规定=（a＞0，m，n∈N*，n＞1）；

（a＞0，m，n∈N*，n＞1）.

0的正分数指数幂为0，0的负分数指数幂没有意义.

至此，建立了完整的分数指数幂的符号系统及运算法则.

1676年牛顿将正整数指数幂一下扩充到有理指数幂，并创立了科学的负指数与分数指数符号，可谓“天衣无缝”，把有理数指数的表示演绎得完美无缺！

评注：（1）从历史上看，由整数指数幂向分数指数幂的跨越是思维的一大障碍，其表示方法也经历了诸多变迁，本环节的设计正是基于这一思考.

①由正整数指数幂到整数指数幂，再到分数指数幂，其过程与数系的扩充相贴合，符合学生的认知结构.

②由于教学时间限制，不可能也没必要全面再现分数指数符号的形成过程，因此只选择了一个已成定论的符号，让学生去揣摩其含义，去体会“规定”的合理性和兼容性.

（2）学生对符号的解释为.这一解释令人兴奋，它将分数指数幂和根式有机联系起来，彻底沟通了两个概念，是一个突破性的思维，极具创新意味.

（3）简要说明负指数和分数指数的历史，旨在表达该符号的历史渊源和美学价值.

3.数学理论

（2）运算法则：

a·ras=ar+s；（a）rs=ars；（ab）r=arbr.

其中r，s∈Q，a＞0，b＞0.

评注：以言简意赅的形式给学生提供完整的知识框架.正如布鲁纳所说：任何知识都可以用一种简单明了的形式呈现出来，使每个学生都能理解.任何一门学科也都有它的基本的知识结构.学生学习的主要任务是掌握该学科基本的知识结构，在头脑中形成相应的知识体系或编码系统.

4.应用

例2 求下列各式的值：

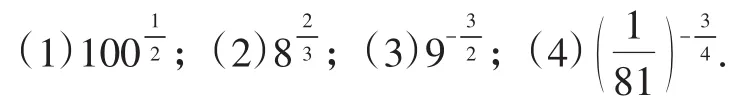
评注：（1）熟悉分数指数幂的简单运算.

例3用分数指数幂的形式表示下列各式（a＞0）.

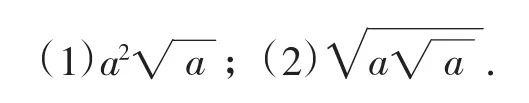
评注：（1）本题着眼于根式与分数指数幂之间的相互转化.

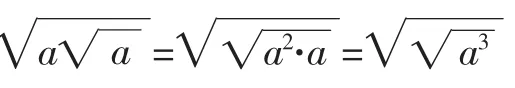
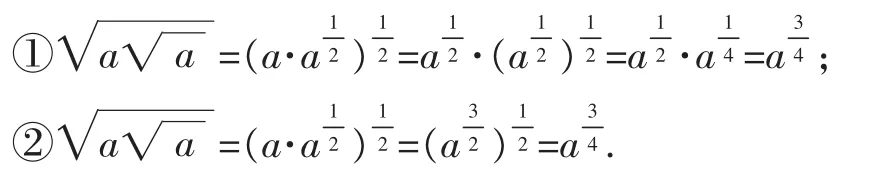
通过用不同方法计算，使运算法则的运用落到实处.

（3）本题是培养学生运算能力的绝好素材，各步运算宜慢不宜快，每一步应让学生“说”出运算的依据！（即算理明确）

三、归纳总结提高

1.逻辑的角度

（1）本节课我们学习了根式、分数指数幂及其相互转化；分数指数幂的运算法则.

（2）体会数学规定的合理性与兼容性.

2.历史的角度

探寻数学符号创立的历史足迹，展示了数学符号的简洁与美观，彰显了数学符号创立的艰辛和智慧.

评注：数学教学中的两种“为什么”：一种是逻辑上的“为什么”，此类“为什么”用逻辑推理的手段解决；另一种是历史上的“为什么”，此类“为什么”只有通过历史知识才能解决.

综上，分数指数是数学符号教学的标本，这一标本不是躺在尘封的历史中，而是活在富含文化意味儿的课堂中，存在于学生鲜活的记忆中，从分数指数的教学中可以一窥数学符号教学的规律和价值，有利于确立学生的符号意识.

1.徐品方，张红.数学符号史［M］.北京：科学出版社，2006.

2.汪晓勤.为什么称未知数为“元”［J］.数学教学，2012.8.