基于GPS动态相对定位的数据处理方法的研究
2013-07-25王世进秘金钟李得海
王世进,秘金钟,李得海
(1.辽宁工程技术大学,辽宁 阜新 123000;2.中国测绘科学研究院,北京 100830)
1 引言
实现高精度GPS定位一般是通过载波相位的双差模型获得,因为双差模型在短基线的情况下可以较好的消除包括电离层延迟在内的多种误差,而其中确定整周模糊度是GPS高精度定位的关键,在确定了整周模糊度后,可迅速得到厘米级的定位结果。在GPS定位的之前必须确保观测数据是“干净”的,就是要对数据进行预处理,包括粗差探测和剔除,除此之外对于高精度的GPS定位一般采用的是载波相位的数据,要得到固定的整周模糊度,其前提是探测和修复周跳,本文给出了一种在动态情况下实用的探测和修复非差载波相位周跳的算法和计算流程。GPS动态相对定位中的关键问题是整周模糊度的确定,由于在动态情况下,双差方程中的坐标参数在不断变化,而只要卫星不发生变化,周跳修复后的模糊度就不发生变化,所以本文利用W-M组合的方法,先不考虑坐标参数,计算出宽巷模糊度的浮点解,由于伪距值的噪声比较大,所以需要多历元的数据进行平滑以减弱噪声等因素的影响,计算出的宽巷模糊度的浮点解的精度可以达到搜索所要求的精度,最后利用自编的程序计算了实测数据,经过对实例定位结果的分析对比,验证了本文提出方法的有效性。
2 GPS动态数据的预处理与周跳的探测修复
GPS动态数据的预处理是需要实时完成的,这就要求采用尽可能少的历元数据进行计算,本文采用两个历元的数据进行计算,构造一个由相邻历元观测数据组成的函数关系式,当函数值的变化超过所设定的阈值时,就可以进一步判断是否含有周跳还是粗差。然而利用两个历元的数据可以探测出粗差或者周跳,但是却不能确定是否是粗差或者周跳,所以还需要第三个历元的数据进行判断究竟是粗差还是周跳。由于不同的函数关系都有不同的适用范围,所以本文采用了以下三种相互补充的观测值函数关系,以正确有效地探测周跳,处理粗差。
2.1 码伪距与相位组合法
载波相位伪距和码伪距的非差观测方程为
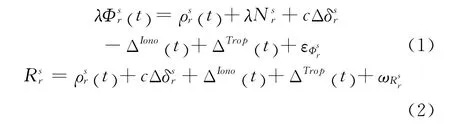
式中,λ为载波的波长,Φ为载波相位观测值,R为伪距观测值,N为非差整周模糊度,ρ为卫地距、ρ中包含坐标参数,ΔIono为电离层延迟误差,ΔTrop为对流层延迟误差,ε为L1载波观测值噪声,ω为伪距观测值噪声。
用式 (1)-式 (2),经过变换得到第i历元非差模糊度的值

式 (3)中,等式右边消去了除电离层外的时间相关误差项并忽略观测噪声,同理可以得到下一个历元的非差模糊度值,和上一个历元求差,由于电离层在相邻的历元变化量很小,可以忽略,由此得到

式 (4)是非差模型下的相位伪距组合法的关系式,忽略非差模型的多路径误差,其组合值主要受伪距和相位观测精度的影响,由误差传播定律可以得到

伪距和载波的精度分别为MR≈±0.29m,MΦ≈±0.01m,所以MδN≈2.2周,所以以3倍标准差作为载波伪距组合法的阈值,可以检测大约8周以上的周跳值。利用码伪距与相位组合法探测出L1或者L2载波上的8周以上的大周跳,修复大周跳后可以把周跳限定在一个比较小的范围内,同时解决了利用电离层残差法会产生的多值性问题,然后联合电离层残差法和M-W组合法探测小周跳并进行修复。
图1和图2分别是不含周跳和含周跳的伪距相位组合的模糊度历元间的变化图,其中图2的第338历元含有10周的整周跳变。
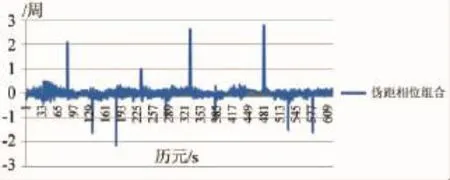
图1 伪距相位组合历元间变化值 (不含周跳)

图2 伪距相位组合历元间变化值 (含周跳)
2.2 电离层残差法与M-W组合法
非差载波相位的电离层残差法即Geometryfree组合

式 (6)中,I是电离层参数,fi是载波相位的频率。相邻历元间的电离层残差变化值可表示为
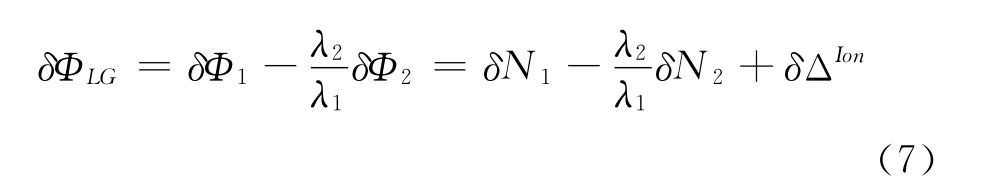
在相邻的历元间,电离层的变化很小,比较稳定的是亚厘米级,所以δΦLG的变化对周跳是很敏感的,所以要设置一个比较合理的阈值,当变化量超过阈值时认为发生周跳,笔者在程序设计时采用的阈值计算公式[4]为

式中,t是历元间隔。
图3和图4分别是不含周跳和含周跳的电离层残差组合观测值历元间的变化图,其中图4的第338和340历元分别含有1周、-1周的整周跳变。
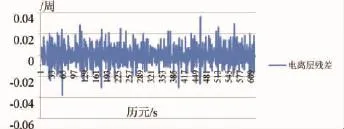
图3 电离层残差历元间变化值 (不含周跳)

图4 电离层残差历元间变化值 (含周跳)
非差载波相位的M-W组合

式 (9)中,Nw是宽巷模糊度,λn是窄巷载波波长,λw是宽巷载波波长。采用递推公式[2]对i个历元的宽巷模糊度进行滤波,可以得到平滑后的宽巷模糊度及其方差

计算第i个历元和第i-1个历元的差值是否大于四倍的标准差,若是,还应继续多判断一个历元,用以确定是粗差还是周跳。
图5和图6分别是不含周跳和含周跳的电离层残差组合观测值历元间的变化图,其中图6的第338和340历元分别含有1周、-1周的整周跳变。
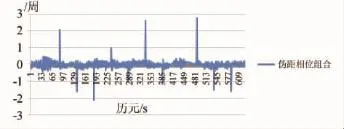
图5 M-W组合历元间变化值 (不含周跳)

图6 M-W组合历元间变化值 (含周跳)
由以上3种不同的观测值组合方式,不仅可以准确的探测周跳,还可以剔除粗差,最后直接给出L1和L2载波上计算非差载波相位周跳的公式

3 M-W组合求解宽巷模糊度
3.1 宽巷模糊度浮点解及其方差
由式 (10)及式 (11)可以看出,W-M组合采用的是宽巷载波和窄巷伪距的观测值组合方式,根据多历元的递推滤波公式可得双差宽巷模糊度及其方差,所以由此可以得到M-W组合的双差宽巷模糊度滤波值及其方差
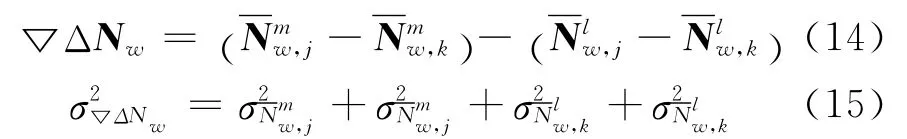
这种双差组合方式不仅适用于短基线,由于M-W组合的双差观测值可以消除电离层延迟、测站卫星几何距离与卫星和接收机钟差的影响,而且双差模型中的观测噪声和多路径的影响可以通过多历元的平滑减弱,所以M-W组合的双差观测模型也是长基线相对定位的常用组合方式。由式(14)及式 (15)得到双差宽巷模糊度浮点解和标准差,由标准差可以确定双差宽巷模糊度的搜索范围,下一步就利用最小二乘搜索方法,搜索固定双差宽巷模糊度。
3.2 最小二乘搜索方法固定宽巷模糊度
双差宽巷模糊度浮点解的精度可由其标准差表示,程序中取4倍标准差作为搜索区间的边界值,对不同的双差宽巷模糊度在区间内取整数值,将每一个模糊度整数向量作为固定解代入宽巷双差观测方程 (式 (16))中进行平差计算,解得坐标值和验后加权方差VTPV,对验后方差最小值和次最小值进行Radio检验,用以确定双差宽巷模糊度固定值。
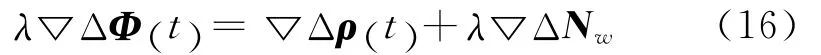
3.3 搜索固定L1载波双差模糊度
由于宽巷载波的波长为0.86m,利用上面的方法很容易固定宽巷模糊度,代入式 (16)可以求得精度较高的坐标值,然后利用L1载波双差相位观测方程可以求出L1载波双差模糊度的浮点解,此浮点解的精度在1-2个周,然后利用最小二乘搜索方法,取±2作为搜索空间的边界值,通过Radio检验可以搜索出正确的L1载波双差模糊度整数解,得到L1载波相位双差模糊度固定解后,代入载波相位双差观测方程中,对于动态GPS相对定位来说,可以迅速令坐标收敛到厘米级的精度,如果没有周跳,模糊度可以传递到下一个历元,以保持厘米级的定位结果。
4 实例分析
根据以上的方法,笔者用C++语言在VS2005编译器下编写了实现程序,在动态情况下主要有坐标的实时变化而带来的算法复杂问题,而本文的定位方法只利用了模糊度信息,避免了这一问题,所以对于静态和动态的数据处理的效果是一样的,故在实例中,笔者采用了北京市房山人卫站的静态数据作为实验数据。
4.1 周跳探测结果分析
采用一段 “干净”的数据,其中并无周跳或粗差,然后分别在G16号卫星的338历元的L1载波上加16周的周跳,在340历元的L1载波上加6周的周跳,笔者用以上周跳探测方法自编程序,对这一段数据进行周跳探测与修复,L1载波的探测结果见表1(表中第一行,1为历元,2为L1原始相位观测值,3为L1相位观测值 (含周跳),4为伪距相位组合法,5为电离层残差与M-W组合法,6为周跳值)。

表1 G16号星L1载波相位周跳探测结果
从表1可以看出,用本文的码伪距载波相位组合联合电离层残差和M-W组合方法探测修复周跳是有效的,而且计算方法简单,易于编程实现。
4.2 静态数据相对定位结果分析
实验数据是采用北京市房山实测的GPS短基线数据,观测时段是2012年7月18日3:00:03~3:46:07(UTC时间),数据采样率为1s,共2765个历元,本文采用天宝TBC软件处理得到了坐标值作为真值与自编程序的处理结果进行对比,利用式 (14)及式 (15)的 W-M组合方法解算宽巷载波整周模糊度浮点解及其方差,固定宽巷模糊度后,把宽巷模糊度的固定解代入双差观测方程中,利用最小二乘原理,很容易得到坐标固定解。由于宽巷组合的观测噪声比较大,这会对最终的坐标影响比较大,所以在固定宽巷模糊度后有必要计算L1的整周模糊度,以提高精度,减小噪声的影响。由宽巷整周模糊度可以求得精度在1-2个周的L1载波双差模糊度的浮点解,利用最小二乘搜索方法可以确定L1载波双差模糊度整数解,采用上述方法可求得L1的固定解,由此可得到BLH三个方向的偏差如图7~图9所示。
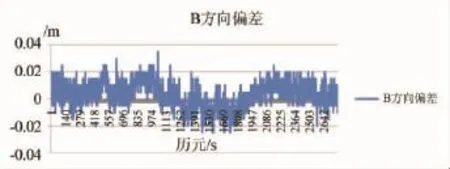
图7 B方向的坐标偏差

图8 L方向的坐标偏差
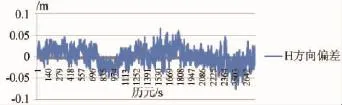
图9 H方向的坐标偏差
5 结语
本文提出一种高精度GPS相对定位的方法,并详细论述了从数据预处理到坐标解算的整个过程和方法,并用自编程序和实验数据验证了本文方法的有效性,本文采用定位方式及程序编写方法是适用于动态情况下的,但是由于动态数据难以验证,所以本文采用的静态数据验证笔者的方法的正确性,这样不仅为自己今后的研究提供了可靠的方向,也给GPS动态相对定位提供了一种有效的参考方法。
[1]霍夫曼-韦伦霍夫B,利希特内格尔H,瓦斯勒E.全球卫星导航系统:GPS,GLONASS,Galileo及其他系统[M].程鹏飞,蔡艳辉,文汉江,等译.北京:测绘出版社,2009:146-178.
[2]方荣新,施 闯,魏 娜,等.GPS数据质量控制中实时周跳探测研究[J].武汉大学学报:信息科学版,2011,34(9):1094-1097.
[3]王 虎,王解先,白贵霞,等.RTK定位模型研究与精度分析[J],大地测量与地球动力学,2010,30(4):113-116.
[4]刘先冬,宋力杰,黄令勇.历元间差分定位模型的粗差探测法探测周跳[J].测绘科学,2011,36(6):58-60.
[5]赵晓峰.基于 M-W 组合的中长基线 RTK定位方法研究与实现[J].遥测遥控,2011,32(6):22-27.
[6]胡丛玮,刘大杰.单历元确定 GPS整周模糊度的分析[J].南京航空航天大学学报,2001,33(3):267-271.
[7]魏子卿,葛茂荣.GPS相对定位的数学模型[M].北京:测绘出版社,1998.
[8]TEUNISSEN P J G.The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J].Journal of Geodesy,1995,70(1-2):65-82.
