GNSS多系统静态基线数据的统一处理方法
2013-07-25王江林文述生
王江林,文述生
(广州南方测绘仪器有限公司,广州 510665)
1 引言
随着北斗卫星导航系统 (BDS)的不断完善,GNSS高精度数据处理领域对多系统数据融合处理的要求显得越来越迫切。同时,出于保密安全的考虑,也需要国内GNSS厂家能提供单独处理北斗二代系统静态数据的随机静态基线处理软件。南方测绘仪器有限公司在国内推出了能同时处理北斗二代系统,GPS和GLONASS的静态基线处理软件。该软件能混合处理三个系统的数据,也能分别单独处理。本文首先简单介绍了多系统数据处理的概况,接着介绍了一种多系统静态基线处理的实现方法,最后用实际数据分析了处理精度。
2 多系统数据处理概况
早在20世纪90年代初,随着GLONASS的不断发展,学术界关于GPS和GLONASS高精度联合处理方法的论文就不断被发表出来。文献[1]分析了GLONASS载波差分的特点及处理方法。对于载波单差方程,GPS和GLONASS的模型是相同的,而对于载波双差,两者却存在差别。主要的原因是GLONASS每颗卫星的载波波长互不相同,导致在处理载波双差观测方程时要相对复杂一些。文献 [1]提出了几种处理策略,一种是以周为单位表达载波双差方程,用接收机钟差来改正因频率偏差导致的额外项;一种是以米为单位表达载波双差方程,接收机钟差通过双差抵消了,但仍然留下了参考卫星单差模糊度的影响,通过单差模糊度的概略值来改正这种影响,达到保留模糊度的整周特性;还有一种方法是将卫星的频率统一到一个相同的值,以达到保留模糊度整周性的目的,但这种方法的波长很短,几乎不可能得到固定解。
文献 [2]详细介绍了GPS/GLONASS组合在高精度大地测量中的应用,并提出了一种递归模糊度固定方法。首先固定波长差较小的双差模糊度,因为波长差越小,参考星的单差模糊度的影响就越小。然后利用固定的双差模糊度来反算单差模糊度,得到精度较高的值,再固定波长差较大的双差模糊度。
3 统一的数据处理方法
通用的静态基线解算过程为:首先根据选择的数学模型建立观测方程,然后根据估计方法(如最小二乘或Kalman滤波)得到浮点解,再根据模糊度浮点解及其方差协方差阵固定模糊度(使用LAMBDA方法或其他模糊度搜索方法),最后计算模糊度固定解,固定解为最终的基线解。常用的双差观测方程如下式所示[3]
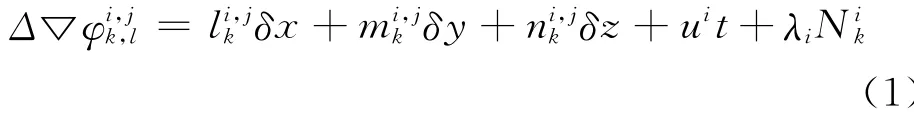
式 (1)中电离层没有参与考虑,多路径、轨道误差等没有表示出来。对流层参数为可选参数,一般在解算长基线时考虑。相位观测值可以为L1、L2的相位观测值,或无电离层组合相位观测值。后者由于观测值中不含一阶电离层延迟(电离层延迟被很大程度上削弱),一般用于长基线解算。
由于北斗二代系统与GPS系统都运用了码分多址 (CDMA)技术[4-5],因此所有卫星的同频段波长是相同的。所以北斗二代系统可以使用和GPS相同的观测方程来建立模型。需要注意的是,北斗二代系统和GPS系统需要在各自系统内选择参考卫星。
GLONASS系统与北斗二代系统和GPS系统均不同,采用频分多址 (FDMA)技术,使得每颗GLONASS卫星的波长都不相同[6]。所以GLONASS系统不能直接使用式 (1)的观测方程来建立模型。要联合使用GLONASS系统,需要在式 (1)的基础之上做如下修改[1])

式 (2) 在 式 (1) 的 基 础 之 上 增 加 了Δλi,j。式 (2)中,Δλi,j为卫星i、j的波长之差,j为参考卫星,为测站k、l参考卫星的单差模糊度。
式 (2)只是用于L1、L2的独立解算。对于无电离层组合,则应使用下式
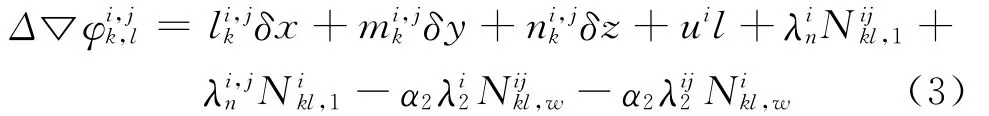
为了统一北斗二代系统、GPS和GLONASS三种系统的观测方程,本软件对式 (1)、式 (2)及式 (3)做了相应的修改,使用下式所用的观测方程
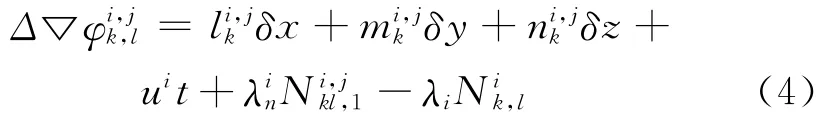
这种方法仍然以双差观测方程来建立模型,以消除卫星和接收机钟差误差。唯一不同的是,模糊度参数选取单差模糊度,而非双差模糊度。这样避免了卫星波长差所导致的影响。采用式(4)所用的观测方程,可以将北斗二代系统、GPS和GLONASS的数据处理方式统一起来。这种统一的数据处理方式即可以单独处理这三种系统,也可以联合处理它们的组合。
4 实际应用与结果分析
为了检验这种统一数据处理方法的正确性,本文处理了4组测试数据,并对结果进行了分析。
第一组测试数据为零基线数据,采集时间为北京时间2012年3月31日13:00,同步时间为36min,采样间隔为1s。数据同时含有北斗二代系统和GPS双频观测数据 (载波相位和伪距)。本文分别单独用GPS、单独用北斗二代系统及混合解 算模式进行处理,结果见表1。

表1 零基线解算结果 (mm)
从表1中可以看出,GPS独立解和BDS独立解精度相当,而组合解的精度介于GPS和BDS之间。
第二组测试数据只含有BDS观测值,以验证北斗独立解算的精度。采用三台BDS接收机采集静态数据,组成闭合环,通过闭合环差值来验证解算精度。观测时间为北京时间2012年4月6日09:23,同步时间为80min,处理采样间隔为15s。解算结果如表2所示。
从表2的结果可以看出,闭合环差都在1mm以内。对于这组短基线数据来说,L1解最优,L2解次之,无电离层组合解精度又低于L2解。

表2 短基线BDS独立解闭合环差值 (m)
第三组测试数据的基线长约11km,观测值含有GPS和BDS数据。观测时间为北京时间2012年3月16日13:15,同步观测177min,处理采样间隔为30s。为了验证GPS和BDS的兼容性,分别解算GPS解,BDS解和 “GPS+BDS”解,解的方式采用无电离层组合解并估计对流层。

表3 11km基线解算结果 (m)
从表3的结果可以看出,这三种解的基线分量最大差值在Y方向上,约1.3cm。而边长差最大约9.1mm。三种解的互差都在允许范围内。
第4组数据基线长约为1km,含GPS和GLONASS观测数据。观测时间为北京时间2011年11月26日14:12,同步观测时间为170min,处理采样间隔为30s。分别解算了GPS解、GLONASS解以及GPS和GLONASS联合解。解的方式采用无电离层组合解,未估计对流层。解算结果如表4所示。

表4 1km基线GPS、GLONASS解算结果 (m)
从表4的结果可以看出,GLONASS的独立解与GPS独立解和GPS与GLONASS的混合解相差稍大,这可能与GLONASS采用FDMA方式有关。
以上4组测试数据的处理,包含了GPS、GLONASS和北斗的独立解和混合解。从数据处理结果可以看出,本文所提出的GNSS多系统统一数据处理方法的正确性。
5 结束语
多系统的联合使用是未来GNSS高精度测绘领域的发展方向。本文根据各系统的特点,提出了一种统一的联合数据处理方法,并根据实际的数据验证了这种方法,结果表明这种方法是正确可靠的。目前,本数据处理方法已在南方测绘仪器有限公司的静态后处理软件中实现。
[1]LEICA A,BESER J.Aspects of GLONASS Carrier-phase Differencing[J].GPS Solutions,1998,2(1):36-41.
[2]HABRICH H.Geodetic Application of the Global Navigation Satellite System(GLONASS)and of GLONASS/GPS Combinations[D].Berne:Astronomical Institute,University of Berne,1999.
[3]HOFMANN B,LICHTENEGGER H,COLLICS J.GPS Theroy and Practice[M].New York:Springer-Verlag,1992.
[4]中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1I:1.0版[EB/OL].[2012-12-28].http://www.beidou.gov.cn/attach/2012/12/27/2012122755318f7eabbe451aa6d052f829f92e50.pdf.
[5]ICD-GPS-200C-4[S/OL].(2000-04-12)[2012-12-28].http://www.navcen.uscg.gov/pubs/gps/icd200/icd200cw1234.pdf.
[6]GLONASS-ICDv5.0[S/OL].(2008-01-01)[2012-12-28].http://facility.unavco.org/data/docs/ICD_GLONASS_5.1_(2008)_en.pdf.
