GPS高程在隧道高程控制中的应用研究
2013-07-25杨渊,施昆
杨 渊,施 昆
(昆明理工大学 国土资源工程学院,昆明 650093)
1 引言
分布在野外的高等级水准控制点由于缺乏维护以及长期的自然或人为破坏,很多都受到了毁坏或发生了位移,已经失去了使用的价值。随着近年来国家对基础设施建设的大力投入,对工程测量方面的需求在日益增加;而云南特有的多山地理环境特点又给测量工作带来了很多困难。因此,如何在这些条件下进行简单高效同时保证作业精度的测量成为了一个越来越重要的问题。在隧道高程控制作业方面,采用了结合GPS高程的三角高程测量方法。
GPS具有全天候、全球性、连续性、实时性和高精度的定位能力,能为用户提供精密的三维坐标,同时无需通视。三角高程测量是一种间接测高法,它不受地形起伏的限制,且施测速度快[1]。这两种作业方式都具有高效易行的特点;GPS提供的高精度高程数据又能弥补高等级水准控制点的缺失。在小区域内,可以假设高程异常值为常数,从而利用GPS静态测量得到的高精度WGS84高程数据对三角高程测量结果进行实时的检核以保证作业精度。本文将结合实例对此方法进行进一步的介绍。
2 结合GPS高程的精密三角高程测量方法
2.1 原理及公式
GPS(Global Positioning System)系统是美国研发的卫星导航与定位系统,已经在测量领域得到了广泛的应用[2]。由GPS相对定位得到的三维基线向量,通过GPS平差,可以得到高精度的大地高差。如果网中有一点或多点具有精确的WGS84大地坐标的大地高程,则在GPS网平差后,可求得各GPS点的 WGS84大地高 H[3]。大地高H于直角坐标Z的换算公式为

式中,N为该点的卯酉圈曲率半径,e为该大地坐标系的第一偏心率。那么AB两点之间的大地高差即为上式求得的各点大地高之差,即HA-HB=△H。
三角高程测量的基本原理为[4]

式中,h为高差,α为竖直角,S为斜距,i为仪器高度,v为目标高度,Cs为地球大气改正数。
GPS测量得到的大地高H,正常高Hr和高程异常ζ的关系式为[5]

2.2 测量方法介绍
当需要在山区进行高程控制作业时,测量人员大多采用外业用GPS与高程控制点联测,内业使用二维约束平差进行高程拟合,然后再用三角高程进行控制网加密方法实施作业[2,4]。而在野外高等级水准控制点被大量破坏以及位移的情况下,可用的高程数据就变得很少;就不可能用GPS进行联测完成水准拟合。当然也有测量工作者探索过在这种条件下的作业方式,采用的是一种叫做GPS三角高程测量的方法[6]。它的思路是根据GPS网的基线改平变长和相应边段上所观测的竖直角,按三角公式计算各GPS点之间的高差,进而求的GPS点的高程。这种方法的缺点在于人工参与计算太多,数据经过繁琐的计算后精度降低很严重,其论文给出的数据结果中高程精度已经完全超出了相关规范的限值;完全没有实际应用价值。
本文采用的方式是首先进行GPS控制网的测量,然后得到无约束平差后的WGS84三维坐标结果。GPS控制点的布设涵盖稳定可用的高程控制点。接下来以一个高程控制点为起算点,实施三角高程闭合水准导线测量;水准路线包含所有的GPS控制点,测量的成果为国家高程基准。在三角高程的测量过程中,用GPS高程数据对测量结果进行实时的检核。这样做的目的在于防止在已知高程数据缺乏的条件下进行总路线长度很长的水准测量时出现错误,从而避免重测与复测提高作业效率。因为整个作业过程采用了两个高程系统,所以就要考虑到不同高程系统的联动。从式(2)中可以知道两个系统之间的关系。考虑到在小区域内影响重力场改正的主要因素,在小区域测量中可以假设高程异常值不变即为常数;理论上大地高差△H等于正常高差△Hr。因此就可以用高精度的大地高数据来检核三角高程测量的正常高数据,即将大地高差作为已知数据和三角高程测量得到的高差进行相减,差值与工程测量相关规范的限值比对,以此来检核三角高程测量的精度是否达标。
3 测量实例
3.1 GPS平面控制网作业
以某高速公路隧道高程控制测量作业为例。整个测区位于云南西部山区中,长约8km,宽约3km;设计方提供的高等级控制点在很大程度上受到了破坏或发生了位移,给隧道施工带来了极大的不便,为此重新布设了高精度的隧道洞外平面控制网。为了保证隧道平面控制网的精度,依据《工程测量规范》中隧道洞外GPS平面控制网的布设规定,将整个平面控制网布设成自由网,考虑到新布设控制网与原坐标系保持一致的原则,选取I4443点作为控制网起算点,采用I4443与隧道另一端比较稳定的点IDD521的方位角作为新设控制网的起算方位。
外业施测使用了4台高精度的拓普康双频双星GPS接收机,严格按照三等GPS测量的要求施测,每个隧道口布设足够数量的点位,共11个控制点。基线向量解算以及三维无约束平差都采用了拓普康的后处理软件Pinnacle进行,同一时段观测值的数据剔除率不大于10%,解算基线的RMS值小于1cm,固定解的比例要比较大,浮动解的比例比较小,全是固定解最好,最大固定解的ratio值要大于95%。本网所有基线解算均为固定解,RMS小于1cm,所有基线最大固定解的ratio值均大于95%。
控制网网形图见图1所示。
无约束平差后的WGS84坐标成果如表1。
I4442与IDD517两点的基线长度见表2。
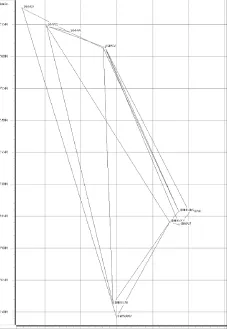
图1 GPS控制网网形图
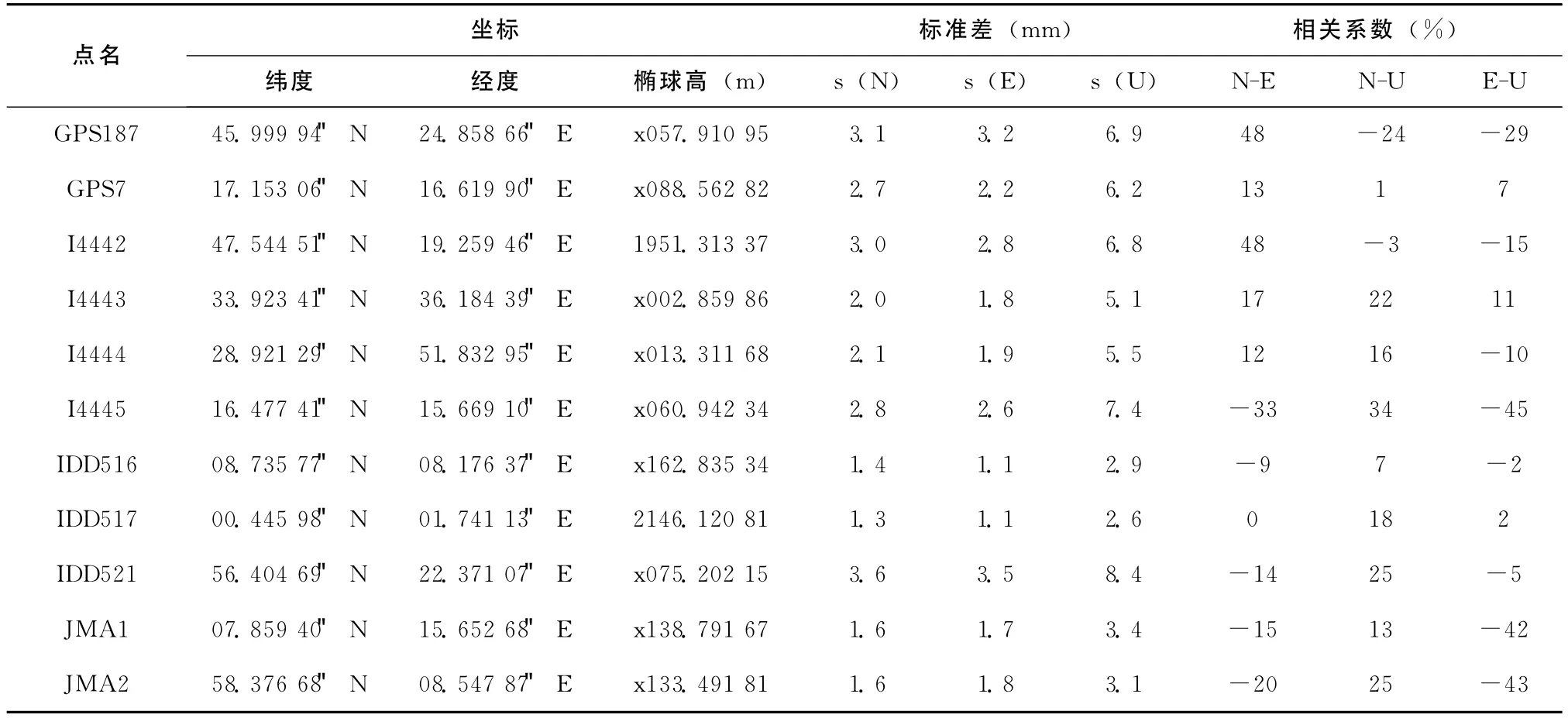
表1 WGS84大地坐标成果表

表2 IDD517与I4442基线长度(m)
3.2 三角高程外业施测方法
外业采用四等光电水准的要求施测,采用设备为拓普康GPT-7501,测角精度为1″,测距精度为 (2mm+2×10-6×D)。以I4442点作为起算点进行往测,经由IDD516止于IDD517总共66个测站。返测由IDD517作为起点,经过IDD516最终抵达隧道另一侧,线路经过I4444、I4443,最终止于I4442构成闭合环。观测成果充分考虑到大气折光的影响,均采用对向观测并记录气象元素,对观测量已进行了加、乘常数改正、边长投影改正、垂直角折光改正、气象改正、地球曲率改正,最终成果高程系统为1985国家高程基准。水准线路略图如图2所示。
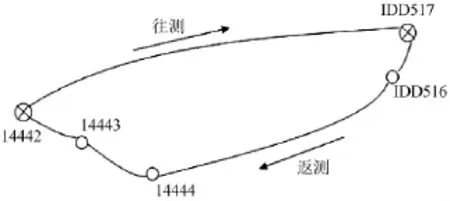
图2 水准路线略图
4 数据分析及比较
在到达IDD517完成往测路线时,在现场用电子手薄和自编的程序进行了三角高程的数据计算并与GPS高程进行了数据比对。
计算结果见表3。
用表1中的数据可以得出WGS84椭球高的两点高差见表4。

表3 三角高程往测结果

表4 WGS84椭球高高差
根据 《工程测量规范》中对于电磁波测距三角高程测量的主要技术要求可知,四等水准的符合或环形闭合差限值为20,D为测距边的长度 (km)。具体要求见表5。

表5 电磁波测距三角高程测量的主要技术要求
由表3可知∑D=11.574 34km,因此限值为68.042 16mm。△h与△h84的差值为0.014 46m,小于规范要求限值。
从以上结果可知往测路线的测量作业满足相关技术要求。于是接着进行了返测路线的测量作业。当整个水准路线测量最终闭合后,内业处理结果表明整体作业的完成精度都很高,同时也就证明了假设是正确可行的。闭合水准路线平差计算结果及精度分析见表6。

表6 闭合水准路线平差计算结果

表7 主要精度数据
每千米高差标准差小于隧道施工相关要求如表8所示。

表8 隧道洞内、洞外高程控制测量等级要求
从计算结果可以看出闭合差与每千米标准差都小于规范限值,其中闭合差甚至小于三等水准要求的限值51mm。
5 结论
在缺乏高等级高程控制点的条件下,如何采用高效易行同时保证精度的方式进行测量作业是一个非常有现实意义的问题。本文的研究结果表明:
(1)可在小区域测量中可以假设高程异常值为常数;
(2)在假设条件下可以用GPS高程作为已知条件实时地对三角高程结果进行检核,达到保证精度的作用,最终结果甚至能优于四等水准的规范要求。
(3)此方法存在局限性,即在假设不能成立的情况下不能用。
[1]杨泽彬,刘宝盈,成会丽.浅析三角高程测量新方法[J].陕西煤炭,2011(2):75-76.
[2]王力军,孟宪军.GPS测量技术和全站仪在山区测图高程控制测量中的应用探讨[J].科技创新导报,2008(16):39-40.
[3]徐绍铨,张华海,杨志强.GPS测量原理及应用[M].武汉:武汉大学出版社,2008.
[4]方允治,赵文聚,仲 鲁.GPS和全站仪在山区高程控制测量中的应用[J].山东交通学院学报,2009,17(3):72-75.
[5]管泽霖,宁津生.地球形状及外部重力场[M].北京:测绘出版社,1981.
[6]冯林刚,赵鹏全.GPS三角高程测量的方法及其应用[J].测绘通报,2006(4):42-44.
