圆柱与刚性平面Hertz接触的临界参数计算

官春平

(广东轻工职业技术学院，广州 510300)

圆柱滚子轴承可以承受较大径向载荷，已经广泛应用于如车辆齿轮箱、机床主轴、减速机以及起重运输机械等比较恶劣的工况中。工程实践表明，Hertz接触理论对于滚动轴承的分析具有足够的计算精度[1-5]。对于圆柱滚子轴承，在正常工况下处于弹性接触状态，其接触宽度远小于接触长度，根据圣维南原理，通过假设接触应力沿滚子素线均匀分布，可以将其接触简化为圆柱与平面的接触模型[6]。1907年，Stribeek R 应用Hertz弹性接触理论建立了滚子轴承在承受径向载荷下的静力学分析模型，获得了滚子最大接触载荷Qmax与径向载荷Fr之间的关系。但在非正常工况下，轴承可能超载运行，此时接触状态可能会发生改变，即由Hertz弹性接触状态向弹塑性接触甚至塑性接触状态改变；如果轴承长期处于弹塑性甚至塑性接触状态，将会严重影响轴承的寿命和传动精度；因此，研究圆柱与平面Hertz接触的临界参数很有意义。

1 圆柱与平面弹性接触理论

根据Hertz理论，圆柱与平面弹性接触时，其接触区域可以简化为长度为L，宽度为2a的矩形，如图1所示。接触应力p分布呈半椭圆柱体形[7]，其为

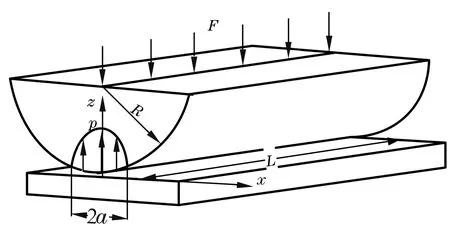
图1 圆柱与平面Hertz接触示意图

(1)

式中：x为接触点距接触中心的径向距离；F为外部载荷。

当x=0时，即接触区域的中心处所受到的接触应力最大，其为

(2)

式中：E*为等效弹性模量，E*=E/(1-ν2)；E为弹性模量；ν为泊松比；R为圆柱体半径。

位于半椭圆柱体中心对称面z轴上点的正应力和主剪应力分别为

(3)

(4)

(5)

(6)

τyz=τzx=0。

(7)

根据接触应力与载荷之间的关系，可得接触半宽a为

(8)

Puttock采用数学简化的方法，推导出圆柱的压下位移的近似解析式为[8]

(9)

2 临界参数计算

根据图1所示的坐标，采用最大接触应力p0对z轴上各点的正应力场进行无量纲化，并且令ξ=z/a，则(3)～(7)式所表示的正应力和主剪应力分别变换为

(10)

(11)

(12)

(13)

从(10)～(12)式可以发现：σx和σz与泊松比ν无关，但σy与泊松比ν相关。z轴上的无量纲应力σx/p0，σy/p0，σz/p0与无量纲位置ξ及泊松比ν之间的关系曲线如图2所示。从图2中可以看出，在接触中心z轴上的所有正应力均为压应力；当ξ<1时，σx，σy和σz的值随深度的增加而快速增大，但泊松比ν的大小对σy值增大的速度有很大影响，在0<ξ<1区域，当ν=0.5时，σy/p0的变化率大约有60%，而当ν=0.1时，σy/p0的变化率却不到10%；当ξ>1时，σx值的变化较小，且最后趋近于0，而σz值随ξ增大而继续增大；随着泊松比ν的减小，材料的可压缩性增大，使得σy值随之增大(这里的σx，σy和σz均为压应力，其值的增大实际为压应力的减小)。

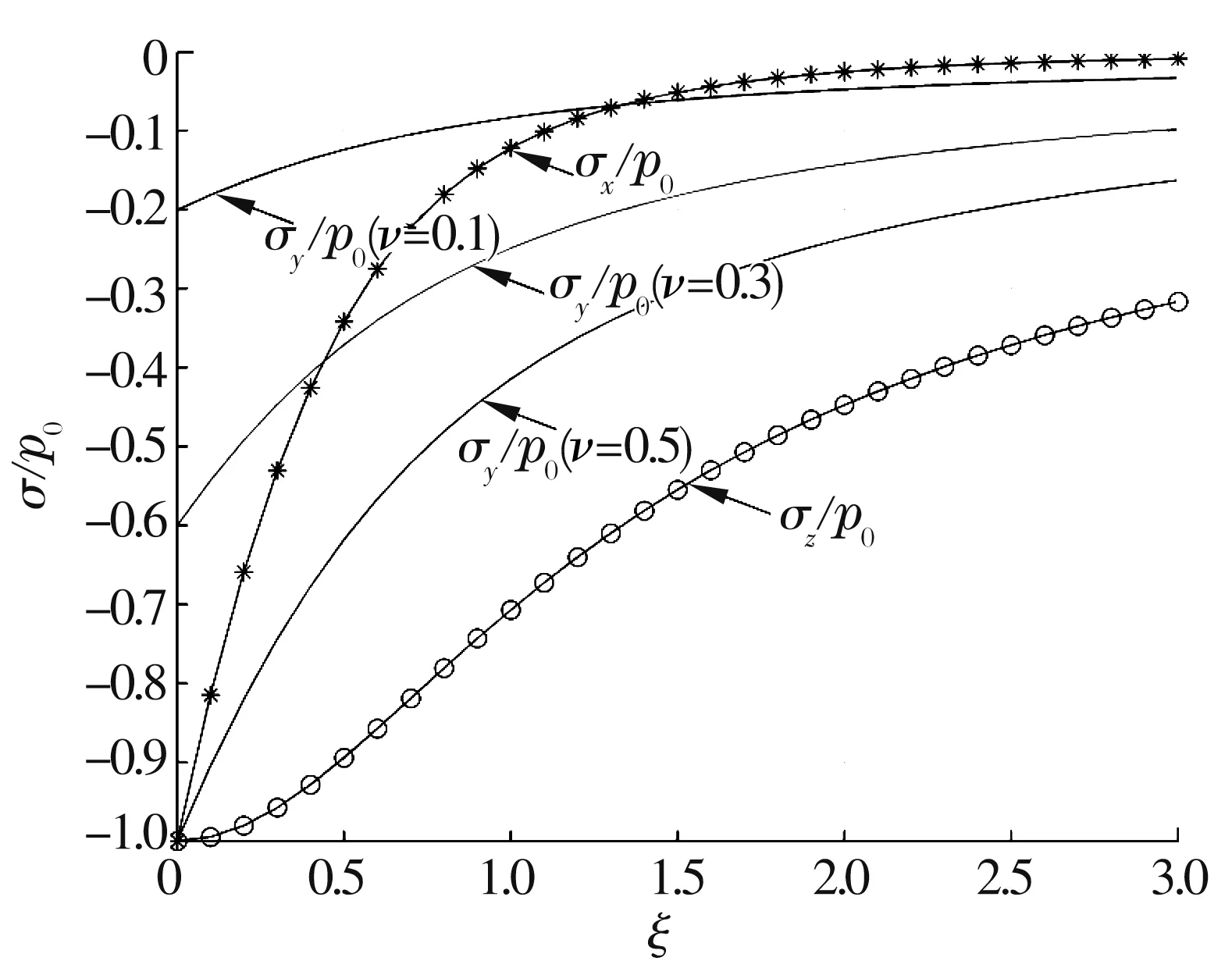
图2 无量纲应力与无量纲位置ξ及泊松比ν之间的关系

在弹性接触过程中，接触应力随着载荷F的增大而增大，最终达到甚至超过材料的屈服强度Y。根据von Mises屈服准则[9]，z轴上点的屈服应力为

(14)

将(10)～(13)式代入(14)式中，有

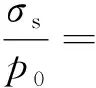
(15)

(15)式表明材料的变形状态(弹性或塑性)与材料所处的位置ξ和材料的泊松比ν有较大关联，其关系曲线如图3所示。从图中可以看出：随着泊松比ν的增大，无量纲屈服应力σs/p0减小，即材料越容易屈服，而且最先发生屈服点的位置由接触中心的正下方向接触区域内部转移；当ν<0.194时，在接触中心表面的材料最先开始屈服；当ν=0.194时，屈服点出现在ξ=0和ξ=0.58处；而当ν>0.194时，最先发生屈服的点已向接触内部转移，出现在接触中心的正下方，即圆柱体中心对称面上；当ν=0.3时，在ξ=0.7处最先开始屈服。当材料出现屈服现象时，此时的圆柱压入位移δc即为材料发生屈服时的临界压入位移。

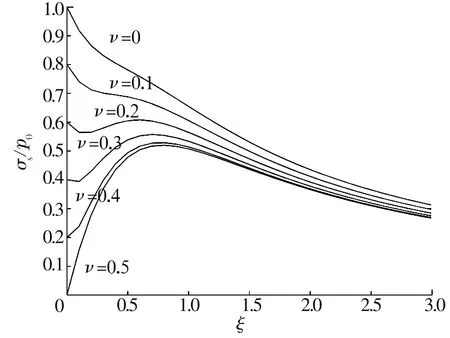
图3 泊松比ν和位置ξ对屈服应力σs的影响

将(15)式对于ξ进行微分，并令该等式为0，即可得到材料发生屈服时的无量纲位置ξ0=z0/a，即

(16)

由于(16)式为超越方程，比较复杂，因此采用数值方法求解。图4为(16)式的拟合曲线。从图中可见，在材料发生屈服时，其拟合函数关系为

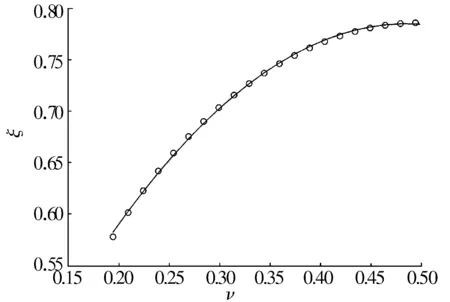
图4 (16)式的拟合曲线

ξm=-2.393 5ν2+2.322 6ν+0.221 6 ，

(17)

其拟合的最大误差为0.77%。

需注意的是，(17)式是在泊松比ν=0.194～0.5下得到的。根据图3所示的泊松比ν对屈服应力的影响，可以看出：当ν<0.194时，初始屈服点位于接触中心表面，即ξm=0。即当

(18)

σs/p0取最大值。

将(18)式代入(15)式，得到一个超越方程，因此同样采用数值方法进行计算，其拟合曲线如图5所示，拟合函数关系为

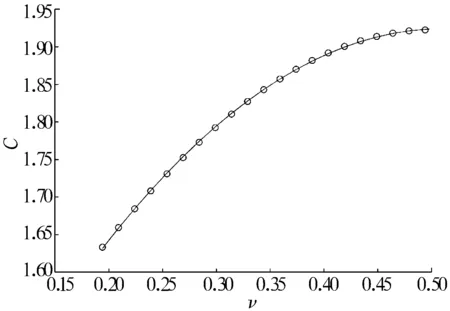
图5 (15)式的拟合曲线

(19)

(19)式的最大拟合误差不超过0.11%。

定义C=p0/Y，则

(20)

因此，圆柱与平面处于Hertz接触时，出现临界屈服的临界参数为

p0c=CY，

(21)

(22)

(23)

(24)

式中：p0c为临界最大接触应力；ac为临界接触半宽；Fc为临界载荷；δc为临界位移。

将(9)式对载荷F进行微分，得

(25)

因此，得到圆柱与平面Hertz接触时的临界法向刚度为

(26)

对于弹性模量E=207 GPa，ν=0.33，Y=355 MPa的普通45#钢，半径为20 mm，长度为100 mm的圆柱，根据(21)～(26)式，可计算得到其与刚性平面发生Hertz接触的临界参数，计算结果见表1。

表1 Hertz接触临界参数

3 结束语

以弹性接触理论和弹性力学为基础，分析了圆柱与刚性平面发生Hertz接触时的应力变化关系，结果表明材料发生屈服时的位置与材料的泊松比有较大关系。采用数值方法获得了材料发生屈服时的位置以及接触中心处的接触应力的表达式。根据Hertz接触理论，建立了圆柱与平面接触的临界接触参数计算式，依据材料的弹性模量、屈服极限、泊松比和圆柱半径及长度，可获得接触区域材料发生屈服时的临界参数。