配对角接触球轴承初始预紧力分析
2013-07-21李鸿亮夏旎邓四二李建华刘良勇
李鸿亮,夏旎,邓四二,李建华,刘良勇
(1.洛阳轴研科技股份有限公司,河南 洛阳 471039;2.河南科技大学,河南 洛阳 471003; 3.北京控制工程研究所,北京 100190)
高温高速工况下,定位预紧角接触球轴承的工作预紧力对轴系动态特性有重要影响,工作预紧力过大,轴承温升较高,限制轴系高速化;工作预紧力过小,轴系抗振动能力较弱,轴承内球易出现陀螺旋转,这是角接触球轴承正常工作下不允许的[1]。该类轴承在高温高速下要有出色的工作性能,必须有恰当的最小工作预紧力,而工作预紧力受离心膨胀、工作温度及有效配合过盈量等因素的影响[2],已与初始预紧力值截然不同,因此,这就需要找到工作预紧力与初始预紧力间的计算关系,通过最小工作预紧力找到最佳的初始预紧力。
1 最小工作预紧力
1.1 防止陀螺旋转的条件
为便于分析,根据角接触球轴承高速旋转时球的运转情况,作以下假设和简化:(1)球稳态运动,忽略加速度项;(2)接触应力和接触变形之间服从Hertz接触关系;(3)内、外圈在外载荷作用下只产生刚性位移。
高速球轴承中球受的各种力和力矩如图1所示。图中Qi,Qe分别为球与内、外沟道间的法向接触载荷;Fi,Fe分别为与陀螺力矩平衡的切向摩擦力;Fc为离心力;Mg为球二维自转时沿y向的陀螺力矩。由图1可以看出,当球在陀螺力矩Mg作用下有转动趋势时,球和沟道之间便产生摩擦力矩阻止这种运动。如果产生的最小摩擦力矩MF≥Mg时,球就不会发生陀螺旋转。因此,为了避免球陀螺旋转,必须满足
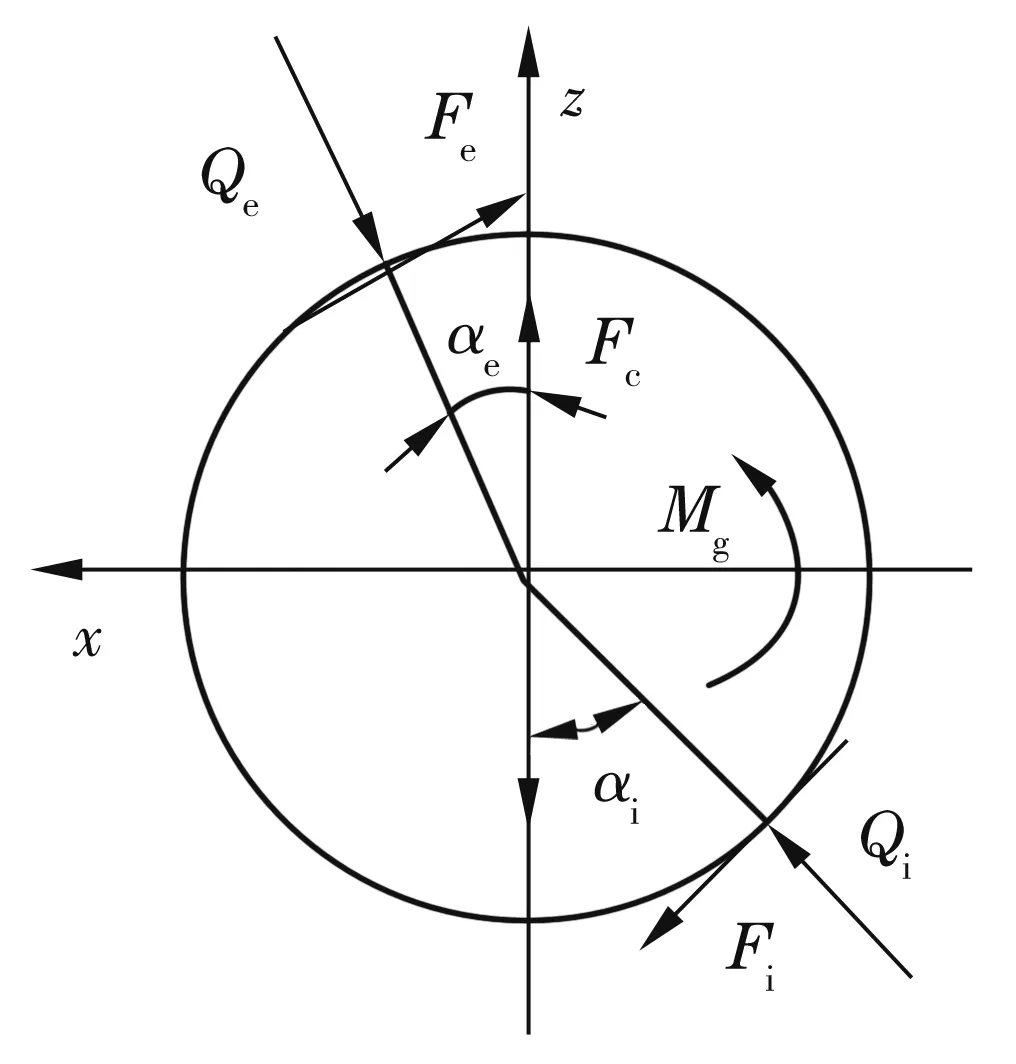
图1 球的力和力矩
MF=0.5Dw(Fi+Fe)≥Mg,
(1)
Fi=Qiμi,Fe=Qeμe,
式中:Dw为球直径;μi,μe分别为球与内、外沟道的摩擦因数。
1.2 陀螺力矩
对于接触角大于零的轴承,球绕两相交的公转和自转轴线旋转时,会受到陀螺力矩的作用。角接触球轴承高速旋转时球的陀螺力矩为
(2)
式中:ωb,ωm分别为球自转和公转角速度;ρ为球的密度;β为自转姿态角,由沟道控制理论求出,或近似地取接触角。
1.3 最小轴向载荷
在高速角接触球轴承中由于离心力作用,多为外沟道控制,此时认为摩擦力只产生在外沟道上,Fi=0[1]。则(1)式可简化为
(3)
则球不发生陀螺旋转时,与外沟道间的最小法向载荷为
(4)
高速球轴承外圈受力平衡方程为[1]
(5)
(6)
式中:Z为球数;Fa,Fr分别为轴向载荷和径向载荷;Qej为第j个球与外沟道的法向接触载荷;αej为第j个球与外沟道的接触角;Mgj为第j个球二维自转时沿y向的陀螺力矩。
角接触球轴承受轴向载荷作用时接触角将增大;径向载荷虽然使接触角减小,但对于角接触球轴承,其影响不大[3]。轴承受载后的接触角可简化计算为
(7)
式中:α0为原始接触角;ri,re分别为内、外沟曲率半径;α为受轴向载荷后的接触角;Kn为载荷-变形常数。
在给定轴承转速、径向载荷等工况下,联立(4)~(7)式,采用Newton-Raphson迭代法可求解出防止球陀螺旋转的最小轴向载荷Famin。
1.4 最小工作预紧力
图2为定位预紧轴承位移-载荷关系曲线,图中两条曲线分别为轴承Ⅰ和轴承Ⅱ的位移-载荷曲线。两条曲线的交点表示在预紧力Fa0作用下,两轴承的轴向位移均为δa0。
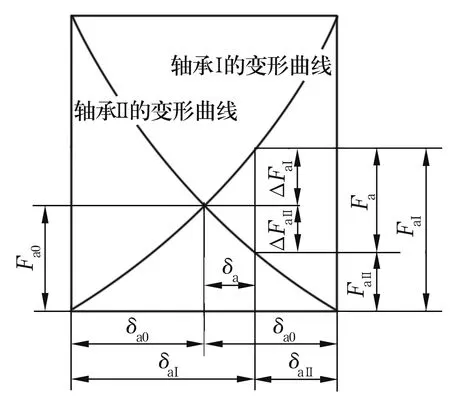
图2 定位预紧轴承位移-载荷曲线
当外载荷Fa沿轴向作用于轴承Ⅰ时,轴承Ⅰ和轴承Ⅱ的内、外圈相对位移均为δa。假设Fa的方向使轴承Ⅰ载荷增加,使轴承Ⅱ载荷减小,从图2可知,此时轴承Ⅰ和轴承Ⅱ的轴向位移分别为
δaI=δa0+δa,
(8)
δaII=δa0-δa。
(9)
相应地,此时轴承Ⅰ和轴承Ⅱ所受的轴向载荷分别为
FaI=Fa0+ΔFaI,
(10)
FaII=Fa0-ΔFaII。
(11)
由力平衡得
Fa=FaΙ-FaII=ΔFaI+ΔFaII。
(12)
显然,为防止球陀螺旋转,必须满足FaII≥Famin,即
Fa0≥ΔFaII+Famin=Fa-ΔFaI+Famin;
(13)
则最小预紧力Fa0min为
Fa0min=Fa-ΔFaI+Famin。
(14)
2 轴承修配初始预紧力
将定位预紧的配对角接触球轴承装入轴系,施加预紧力后再承受其他载荷作用,内、外圈轴向位置近似不变。轴承在与轴、轴承座过盈配合时轴承内圈膨胀,外圈收缩;当轴承内圈随轴一起作高速旋转时,在离心力作用下内圈将产生径向膨胀,改变内圈与轴之间的过盈量;工作中各零件温度的变化将影响套圈与轴和轴承座的配合过盈量;各零件存在温差引起的热变形。上述这些因素均会影响轴承的工作预紧力。文献[2]详细分析了离心膨胀、工作温度及有效配合过盈量对工作预紧力影响。
内圈在高速旋转时,内沟道直径的径向膨胀量δc为
(15)
式中:ρi为内圈材料密度;ω为内圈角速度;Ei为内圈材料弹性模量;νi为内圈材料泊松比;d为轴承内径;F为内沟道直径。
轴承工作时由温度引起的内、外沟道直径和球直径的径向变化量之和δt为
δt=λi(Ti-T0)F+2λw(Tw-T0)Dw-
λe(Te-T0)E,
(16)
式中:λi,λe,λw分别为内、外圈及球材料热膨胀系数;Ti,Te分别为内、外圈工作温度;E为外沟道直径;Tw为球工作温度;T0为室温。
外圈与轴承座以有效过盈量Ike配合时,外圈将收缩,外沟道直径也将减小,其径向减小量δke为[4]
(17)
式中:Ee,Ek分别为外圈和轴承座材料弹性模量;νe,νk分别为外圈和轴承座材料泊松比;D为轴承外径;D2为轴承座外径。
内圈与轴以有效过盈量Isi配合时,内圈膨胀,内沟道直径也将增大,其径向增大量δsi为[4]
(18)
式中:Es为轴材料弹性模量;νs为轴材料泊松比;ds为轴直径。
离心膨胀、工作温度及有效配合过盈量引起的轴承径向游隙的减小量之和δr为
δr=δc+δt+δke+δsi。
(19)
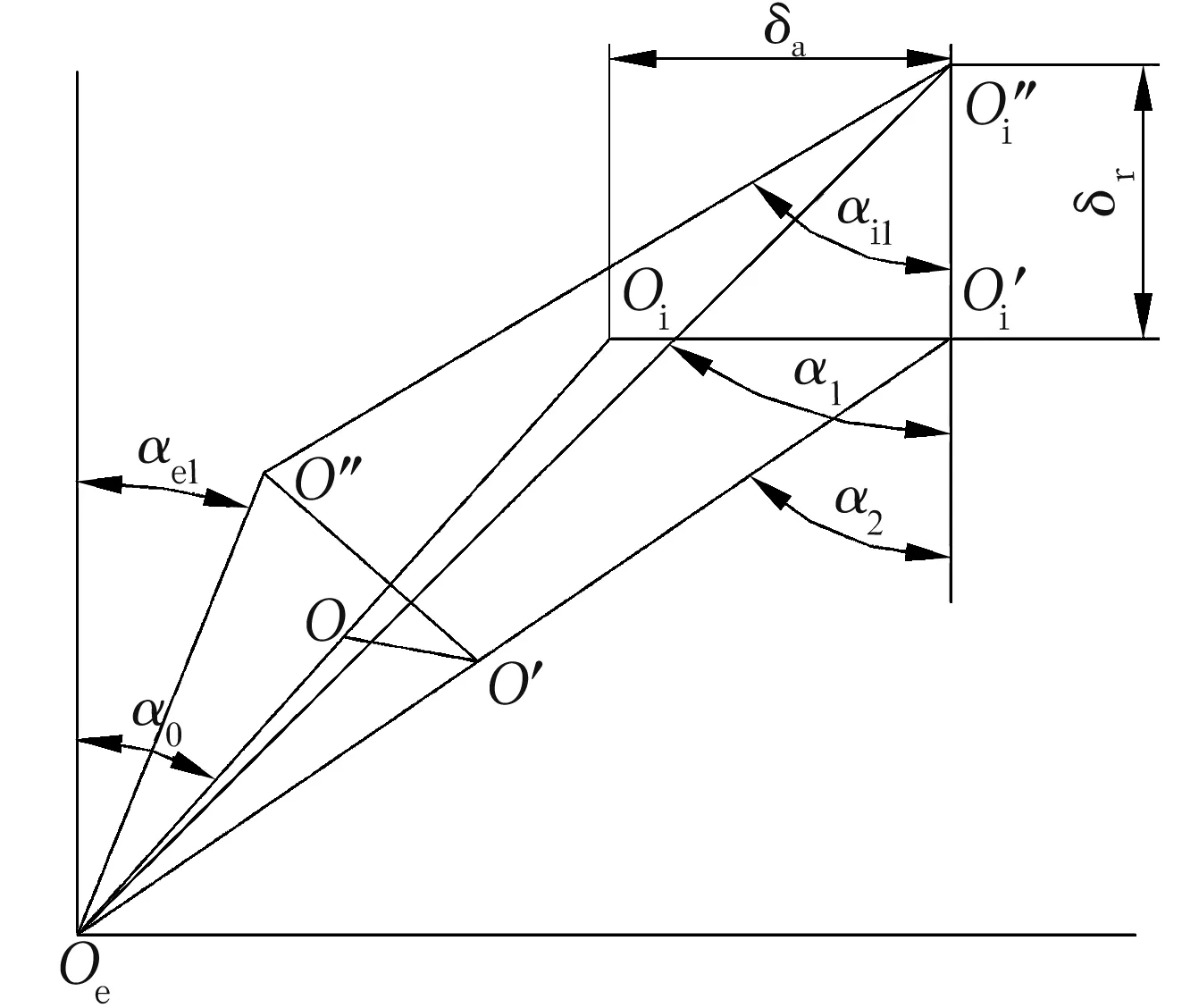
图3 球中心与沟曲率中心相对位置
由图3可知,轴承在工作预紧力Fa0作用下,各球的接触载荷Q及弹性接触变形δ分别为
(20)
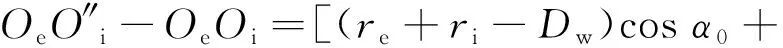
δr]/cosα1-(re+ri-Dw),
(21)
式中:α1为工作预紧力Fa0作用下轴承接触角。
根据Hertz接触理论,接触载荷Q与接触弹性变形δ的关系为
(22)
球和内、外圈总的接触弹性变形δ为[1]
δ=δasinα1+δrcosα1。
(23)
由图3可知,轴承装配预紧后球和内、外圈总的接触弹性变形δ0为
(24)
(25)
式中:α2为预紧后轴承的接触角,此时内、外接触角相等。
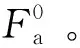
3 实例
以7301C混合陶瓷角接触球轴承为例,轴承参数和受载情况见表1。其转速与所需修配初始预紧力的关系如图4所示,计算时假设轴承内、外圈温差为30 ℃。

表1 7301C轴承参数和承受的载荷
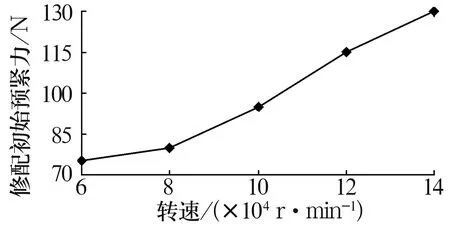
图4 7301C轴承修配初始预紧力与转速的关系
由图4可得,7301C轴承在转速100 000 r/min时,最小初始预紧力为95 N,考虑到计算误差,建议初始预紧力修正为100 N。
4 结束语
依据轴承高速旋转时防止球发生陀螺旋转的条件,给出了轴承最小工作预紧力。在此基础上考虑了轴承高温、高速工况条件的影响,推导了工作预紧力与初始预紧力的关系。结合7301C混合陶瓷角接触球轴承的工况,给出了其初始预紧力的建议值。
