圆锥滚子超精研导辊挡边形面分析

高作斌，陈世友，马伟

(1.西北工业大学 机电学院，西安 710072；2.河南科技大学 机电工程学院，河南 洛阳 471003)

圆锥滚子锥面的无心贯穿式超精研一般是精密圆锥滚子的最后一道加工工序，对保证滚子表面质量、凸度和圆度等技术要求具有重要作用。导辊在超精研加工中起到对滚子进行支撑、回转和贯穿驱动及姿态控制的作用[1]。近年来，高性能轴承及其所用高精度滚子受到重视[2]，圆锥滚子的加工质量成为制约我国高性能圆锥滚子轴承制造的瓶颈，导辊设计与加工的重要性也日益突出。目前对圆锥滚子超精研导辊的研究侧重于导辊形面[3-5]，而对挡边关注较少。实际上，导辊挡边形面与滚子球基面处于推动力作用下的滑动摩擦状态，工况条件较差，两表面之间的摩擦磨损对超精研质量及导辊寿命都有影响。保证挡边形面与滚子球基面之间良好的接触几何关系，减小两表面之间的摩擦磨损，有利于保持滚子自转和贯穿的稳定性，也可以避免加工过程中出现滚子球基面划伤，从而提高滚子加工质量；还可以减轻导辊挡边的磨损，从而减少挡边修磨次数，既省时，又能提高导辊的使用寿命。

下文基于超精研中导辊挡边形面与滚子球基面之间的几何、运动和作用力特征，分析挡边理想形面及简化轴向廓形；基于挡边磨削加工中挡边与砂轮之间的几何及运动关系，对挡边的磨削形面进行分析，对磨床砂轮架垂直摆角的合理选择提出建议。

1 导辊挡边理想形面及其简化

1.1 超精研对导辊挡边的要求

圆锥滚子超精研中，导辊的工作方式如图1所示。前、后导辊轴线水平平行配置，在传动装置驱动下等速同向旋转，对通过上料机构进入导辊之间的滚子进行支撑、引导和驱动，使其在下压且直线振荡的油石下方，一边旋转一边纵向贯穿，实现滚子锥面的超精研加工。导辊的辊形表面通过滚子锥面控制滚子姿态和贯穿轨迹并驱动滚子自转，导辊的螺旋挡边通过滚子球基面推动滚子贯穿[1]。

图1 圆锥滚子超精研导辊工作方式示意图

可见，导辊挡边形面与圆锥滚子球基面之间存在相对滑动，在轴向推力作用下产生滑动摩擦，这种受力和相对运动关系类似于圆锥滚子轴承中内圈挡边与滚子球基面之间的关系[6]，因此，要求导辊挡边形面与圆锥滚子球基面在接触点处相切。

1.2 导辊挡边的理想形面及简化处理

导辊挡边为螺旋形，且滚子轴心线与导辊轴线为空间交错状态，滚子球基面与导辊挡边之间的几何关系比内圈与滚子球基面之间的几何关系更加复杂，导辊挡边形面也不能是内圈挡边那样的锥面。滚子球基面与导辊挡边的几何关系是滚子与导辊几何关系的一部分，受到滚子锥面与导辊辊形面之间几何关系的影响。

滚子与导辊的几何关系如图2所示。超精研中滚子的姿态由其轴心线的姿态确定，假定滚子轴心线只在与导辊轴线平行的铅垂平面内倾斜。设滚子轴心线与水平线的夹角为θ，上素线与水平线的夹角为λ(数值很小，与滚子凸度有关)，滚子半锥角为α。根据图2中B-B视图所示关系，得

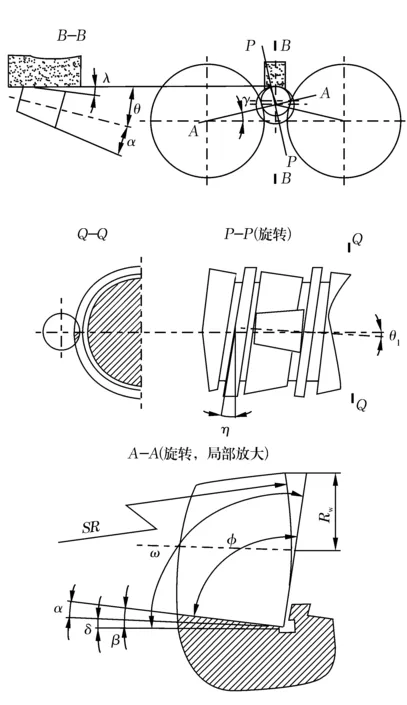
图2 滚子-导辊几何关系示意图

θ=α+λ。

(1)

滚子轴心线与导辊轴心线是空间交错关系，在不同的投影面上，两轴心线的夹角不同，相应角度关系如图3所示。图中，CD和GH分别为导辊和滚子的轴心线；CDEF为水平面；EFGHJ为B-B截面；CDGKJ为A-A截面；GHK为P-P截面；DEJHK和CFG为与滚子轴线垂直的2个铅垂截面；A-A截面与水平面的夹角为滚子大端与导辊的接触角γ；GK为滚子轴心线GH在A-A截面的正投影。基于这些几何关系，得出

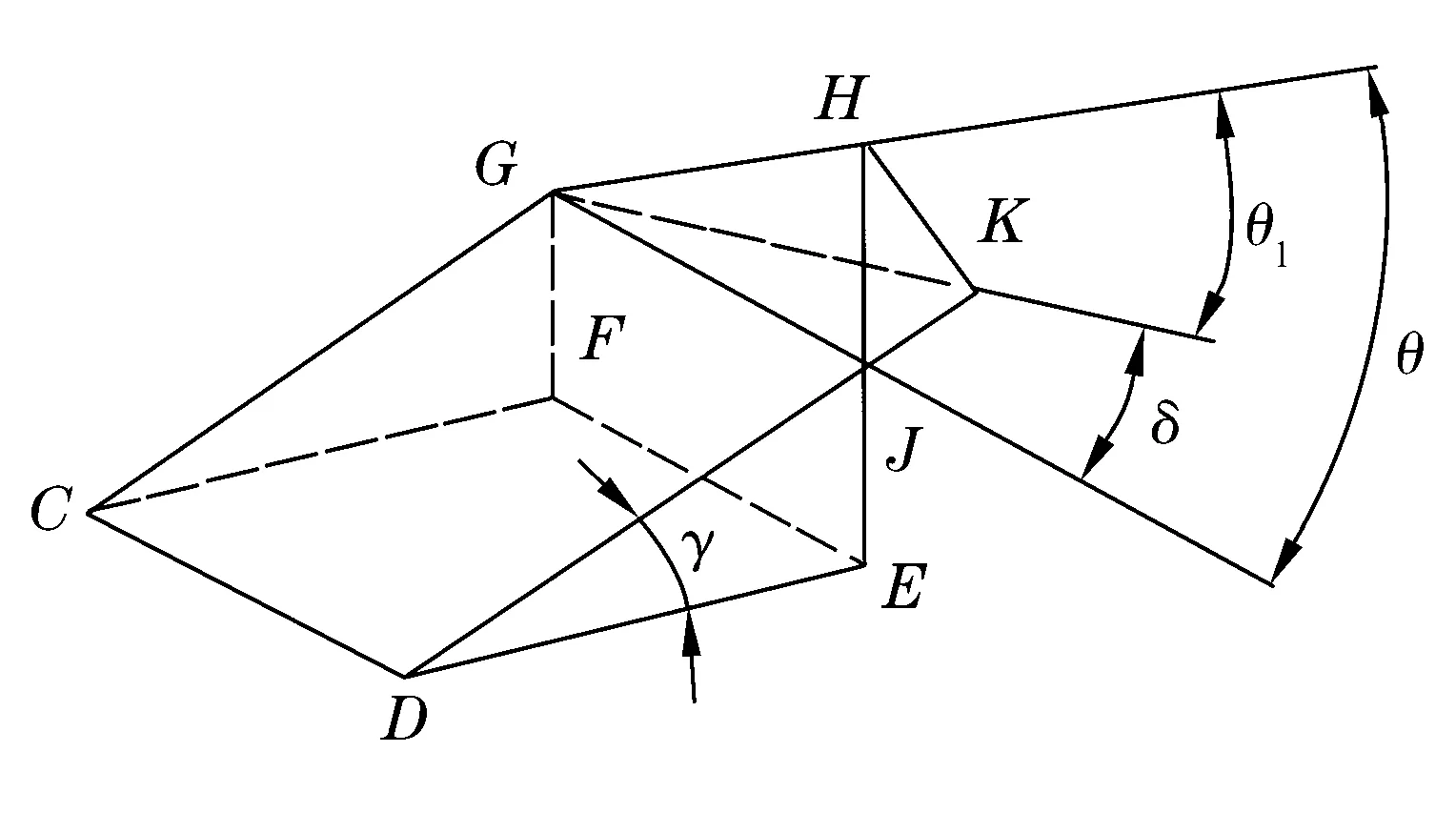
图3 滚子轴线与导辊轴线角度关系示意图

tanδ=tanθsinγ，

sinθ1=sinθcosγ，

式中：δ为经过导辊轴心线和滚子大端圆心的A-A截面内两轴心线的夹角；θ1为经过滚子大端圆心，与A-A截面垂直且与导辊轴线平行的P-P截面内两轴心线投影的夹角。

由(1)式可得

tanδ=tan(α+λ)sinγ，

(2)

sinθ1=sin(α+λ)cosγ。

(3)

图2P-P视图中，导辊螺旋升角η取决于导辊的螺距和直径；由(3)式可知，θ1取决于滚子轴心线倾斜角和滚子与导辊的接触角，不能保证两者相等，因此滚子球基面与导辊挡边螺旋的走向并不一致。例如，取α=2°，γ=16°，λ=0.1°，由(3)式得θ1=2.018 6°；取导辊的螺距和直径分别为60 mm和160 mm，则η=6.807 0°，θ1<η。这种情况下，滚子球基面与挡边的接触点位于图2Q-Q视图所示的网格区域内，而图2A-A视图中的球基面截形线与导辊挡边截形线并不接触。

寻求挡边理想形面需要求出滚子球基面与导辊挡边接触点的准确位置，并对接触点处滚子球基面与挡边螺旋面的局部几何关系进行分析，比较复杂。因此，从工程应用角度考虑，进行简化处理。将图2A-A视图中的滚子球基面截形线上与导辊挡边对应点处的切线，作为挡边的轴向截形线，即把挡边的理想轴向廓形简化为直线廓形。由于挡边扣除越程槽后的高度一般只有2～3 mm, 图2Q-Q视图所示的网格区域并不大，而滚子球基面半径约为滚子大端直径的15倍左右，一般在100～400 mm。因此，接触点在网格区域内变动，滚子球基面上接触点切线倾斜角度的变化很小，简化处理引起的误差也较小。

1.3 挡边简化廓形倾斜角度分析

挡边简化轴向廓形直线对导辊轴线的倾斜角度等于图2A-A视图所示角度ω，可见

ω=β+φ，

(4)

式中：φ为滚子轴向截面内，球基面截形上与导辊挡边接触点处的切线与滚子素线的夹角；β为导辊辊形角。

φ为滚子自身几何参数，主要受滚子半锥角、球基面半径和接触点位置影响。由于接触点位置靠近滚子大端边缘，其实际变动量远小于球基面半径，因此可以用滚子大端半径Rw、滚子球基面半径SR和滚子半锥角α近似计算φ值。根据图2A-A视图所示几何关系，φ的计算公式为

(5)

φ一般略大于90°。

辊形角β的计算有多种公式[4-5]，都比较麻烦。根据图2A-A视图中各角度关系，得

β=α+δ。

(6)

将(2)式代入(6)式得

β=α+arctan[tan(α+λ)sinγ]。

(7)

对该导辊辊形角计算公式与其他计算公式[4-5]进行多种计算条件下的算例对比，结果的一致性非常好，可用于挡边角度计算及导辊辊形角的快速计算。

将(5)式和(7)式代入(4)式，得到

(8)

(8)式即为挡边简化轴向廓形直线与导辊轴线夹角ω的计算公式，可见，ω是钝角。

算例1，以32321E轴承滚子的超精研导辊为例，滚子几何参数为：α=2°，Rw=16.143 mm，SR=439 mm。超精研加工参数取λ=0.1°，γ=16°。由(8)式计算得ω=92.686 5°。

2 导辊挡边的磨削形面

2.1 导辊挡边的磨削形面及其轴向廓形

导辊挡边形面的磨削加工一般在专用的导辊磨床上完成，加工时，导辊在机床工作台带动下旋转并按螺距的要求作轴向移动(还可以作间歇性的轴向进给)，砂轮旋转但轴向固定不动(可以作间歇性的径向进给)。砂轮与导辊的几何关系如图4所示。导辊轴线保持水平且不能调整，砂轮大端中心与导辊轴线等高，砂轮轴线在水平投影面上与导辊轴线平行，在过导辊轴线的铅垂投影面上与导辊轴线存在一个夹角ε，ε就是可根据需要调整的砂轮架垂直摆角。

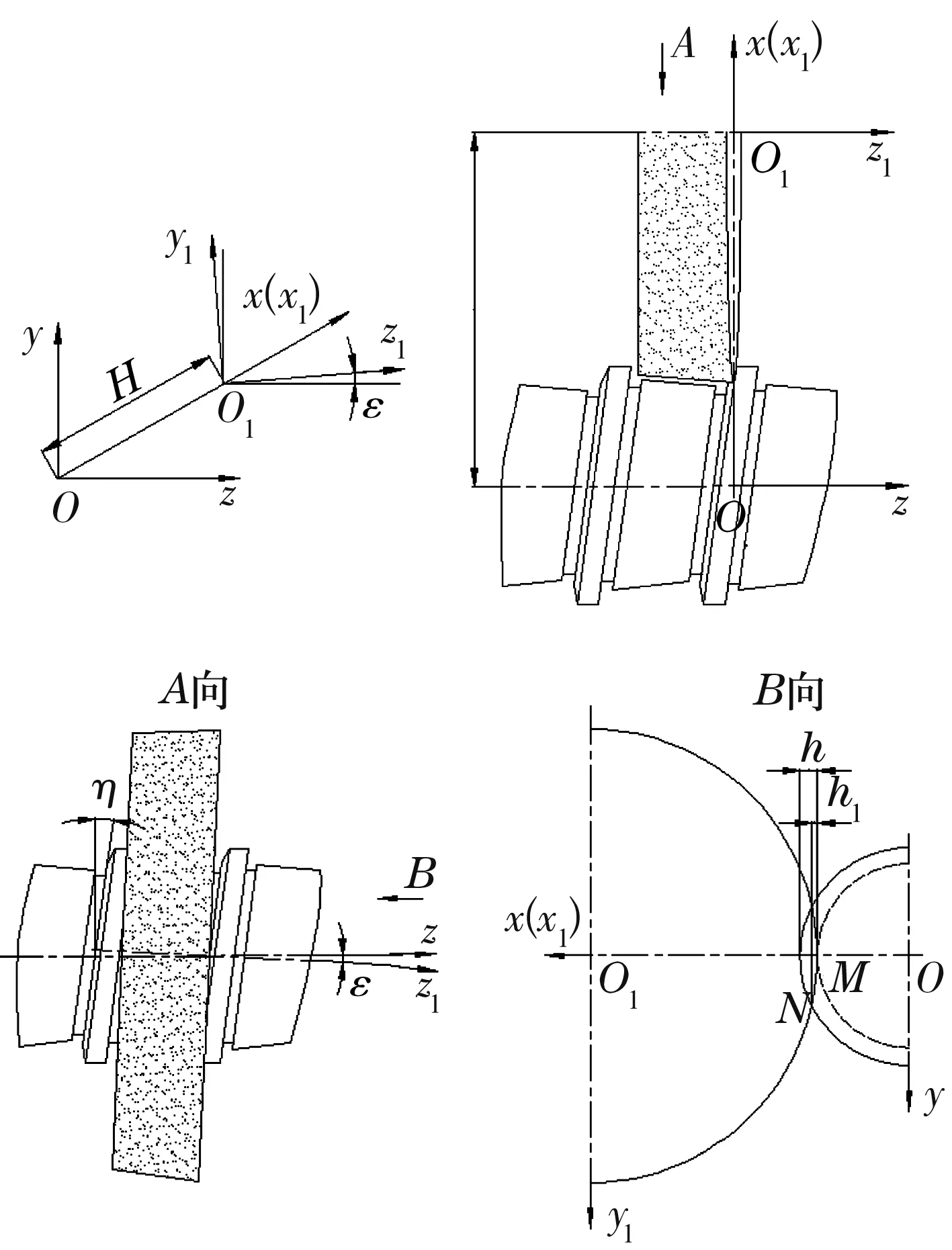
图4 磨削砂轮与导辊几何关系示意图

将图4的A向和B向视图与图2P-P和Q-Q视图对比可以看出，砂轮与导辊挡边的几何关系类似于滚子与导辊挡边的关系，不同之处在于滚子有球基面，而砂轮端面是平面。由于导辊磨床的砂轮是平形砂轮，端面不修整，只修整圆周面，因此，磨削挡边时，起作用的是砂轮大端圆弧，该圆弧与导辊挡边的接触线就是图4中B向视图所示的一段圆弧MN。接触线MN绕导辊轴线作螺旋运动得到导辊挡边的磨削形面。

基于砂轮和导辊挡边几何关系与滚子和导辊挡边关系的相似性，挡边的磨削形面与其理想形面也存在相似性，限于篇幅，此处不详细分析这种相似性，仅分析磨削形面轴向廓形，并与上述简化轴向廓形进行对比。

如图4所示，建立坐标系σ(Oxyz)和σ1(O1x1y1z1),O1为砂轮大端中心，z1轴为砂轮轴线，z轴为导辊轴线，y轴垂直向上，x和x1同轴，O1在x轴的坐标值为H(即导辊挡边高度)。

在坐标系σ1中，接触线MN的方程为

(9)

式中：Rs为砂轮大端半径。

σ1和σ的坐标变换关系为[7]

(10)

利用(10)式将(9)式进行坐标变换，可得在坐标系σ中表示的接触线MN的方程为

(11)

根据图4中B向视图所示几何关系，(11)式中h1为

(12)

式中：h1为中间参数，几何含义见图4B向视图。

对接触线上任意一点P，设其在坐标系σ中的坐标为(x0，y0，z0),则

(13)

跟随P点位置，建立如图5所示的正交坐标系σ2(O2x2y2z2),O2在坐标系σ中的坐标为(0，0，z0),z2轴与z轴同线同向，x2轴经过点P。由图5可知

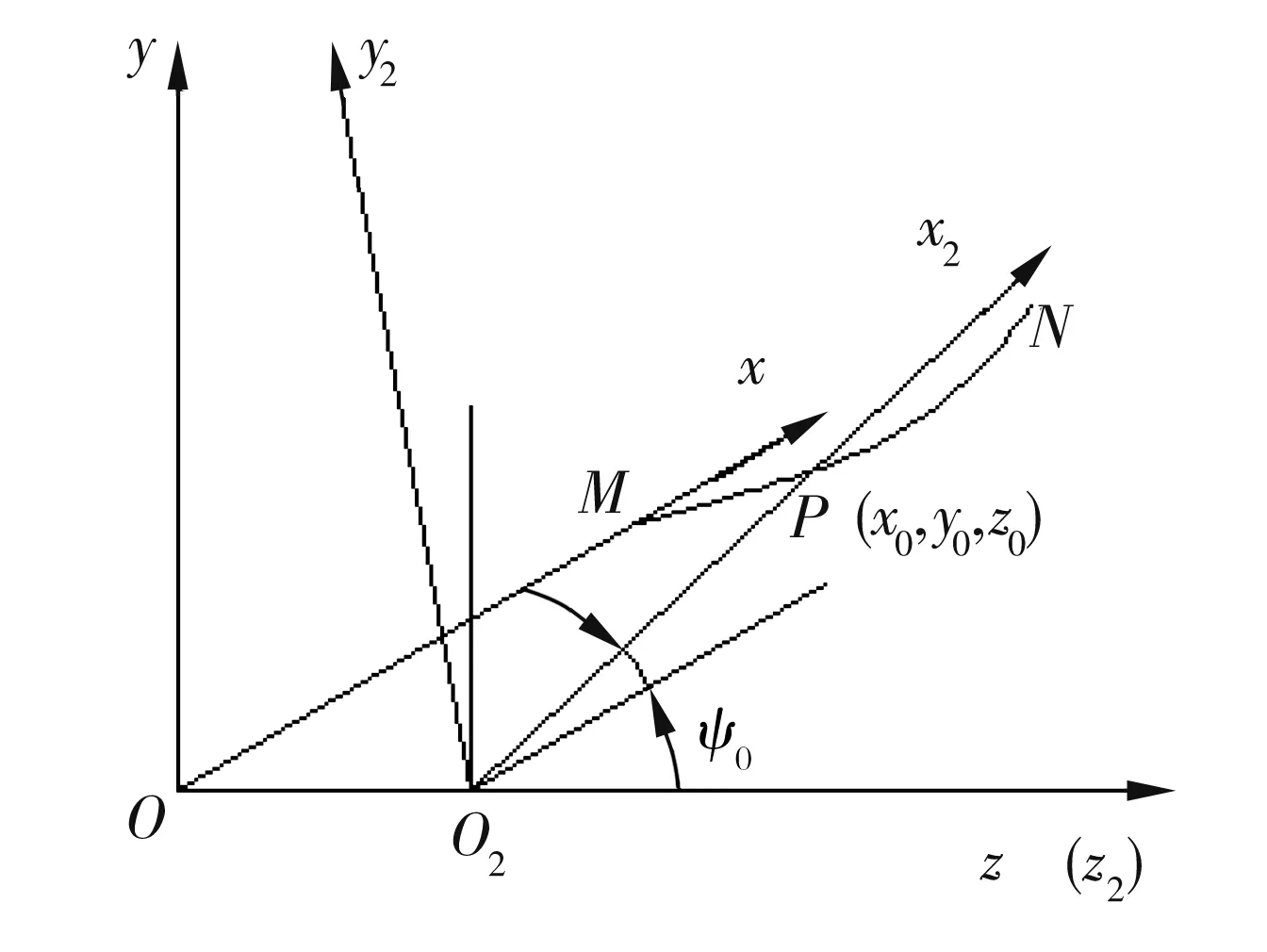
图5 螺旋线和螺旋面方程坐标系

(14)

式中：a为点P到O2的距离；ψ0为x2轴与x轴在O2x2y2平面正投影的夹角。

点P绕z轴或z2轴作螺旋运动形成螺旋线，在σ2中，该螺旋线方程为[8]

(15)

式中：ω0和v0分别为形成螺旋线的匀速圆周运动角速度和匀速轴向移动速度。根据圆柱螺旋线的几何特征，得

(16)

式中：s为导辊的螺距。

σ2和σ的坐标变换关系为

(17)

利用(17)式对(15)式进行变换，利用(14)和(16)式进行整理，并将结果与(13)式并列，可得在坐标系σ中表示的挡边磨削形面方程为

(18)

式中：L为导辊长度。

在(18)式中，令y=0,x=Rz，并将(12)式列入，可得磨削挡边的轴向廓形方程为

(19)

式中：Rz为导辊挡边轴向廓形半径。

根据图4所示砂轮轴与导辊轴的间距关系，得

Rzmin=H-Rs，

(20)

式中：Rzmin为导辊挡边轴向廓形半径最小值。

由(19)式可知，磨削挡边的轴向廓形比较复杂。因此，通过数值分析算例考察其形状和倾斜角度。

算例2，取H=250 mm，Rs=170 mm，h=3 mm，s=60 mm，ε分别取2°，4°，6°和8°，根据(19)式计算得相应的磨削挡边轴向廓形如图6所示，由(20)式计算得Rzmin=80 mm。

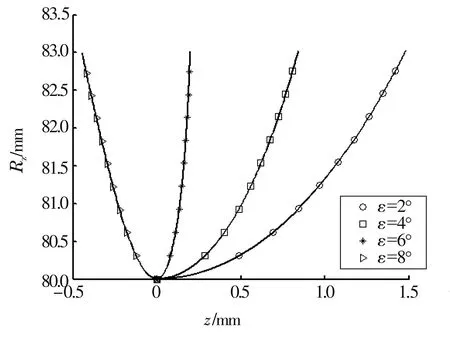
图6 导辊磨削挡边的轴向廓形

由图6可知：

(1) 磨削挡边的轴向廓形并非直线，但可以看作是由一小段曲线和一大段近似直线两部分组成。在Rz最小值附近，廓形非线性比较严重，属于曲线段；而在偏离Rz最小值约0.5 mm后，廓形接近直线，属于近似直线段。这种性质表明导辊挡边磨削中，应使砂轮越过挡边的越程槽约0.5 mm。

(2) 磨削挡边的轴向廓形相对z轴的倾斜方向和角度，对砂轮架垂直摆角ε十分敏感。这种性质指出导辊挡边磨削时合理选择砂轮架垂直摆角ε的重要性。图6中ε=8°时，廓形倾斜方向已经改变。

2.2 砂轮架垂直摆角的选择

将挡边简化轴向廓形(直线)作为设计廓形，其倾斜角度ω由(8)式计算(ω是廓形与z轴反方向的夹角)。算例1中ω=92.686 5°，下面计算磨削廓形近似直线段与z轴反方向的夹角ωm，通过调整砂轮架垂直摆角ε使ωm与ω接近。计算ωm时，取Rz=83 mm和Rz=80.5 mm时廓形上两个点的连线作为近似直线段。

算例2中，在最小挡边半径处，螺旋升角η=6.807 0°。由图4中A向视图可知，当ε=η时，砂轮端面与挡边螺旋走向一致，磨削挡边与导辊轴线夹角接近90°，因此，使ε取值在η附近变动，考察挡边廓形的变化，寻求ωm与ω接近时的ε值。

图7为ε取值在η附近变动时的挡边轴向廓形，计算条件除ε外与算例2相同。各廓形的ωm值见表1。由图可知，当ε=η时，ωm实际上小于90°，与ω并不接近；而ε=5.8°时最接近。据此，进一步减小ε取值的变动范围和变动间隔，得到图8所示ωm与ω更加接近的一组廓形，各廓形的ωm值见表1。

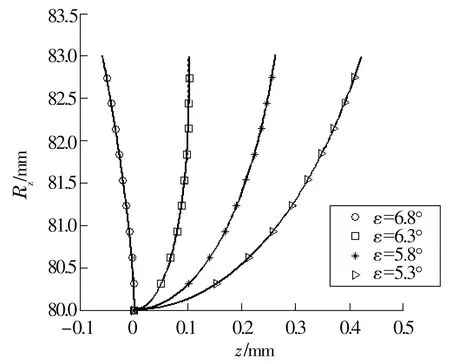
图7 ε取值在η附近变动时的挡边轴向廓形

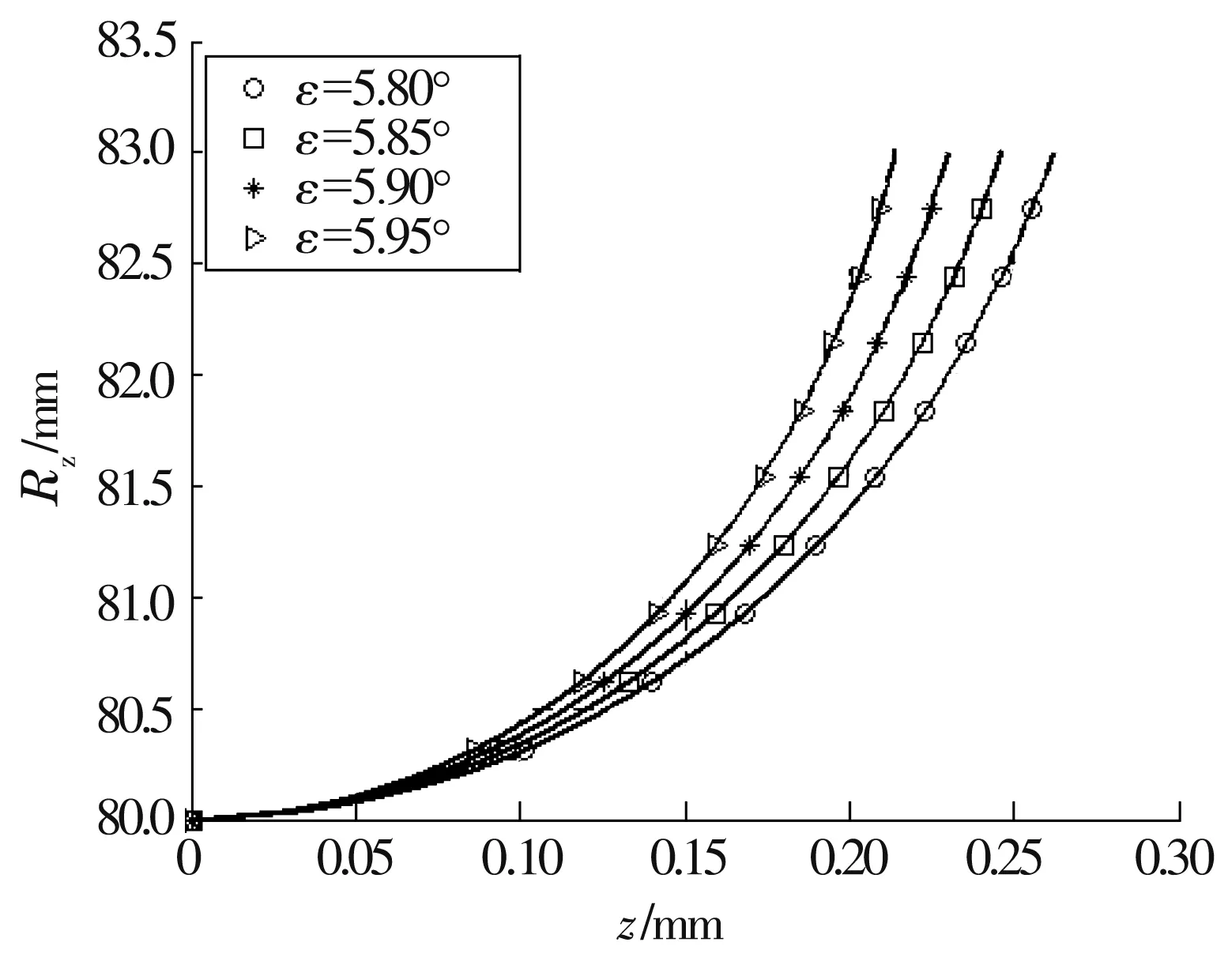
图8 ωm与ω接近时的挡边轴向廓形

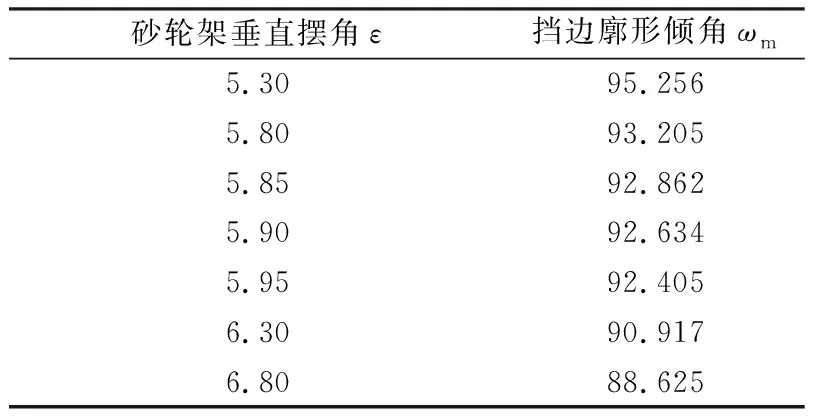
表1 ε取不同值时挡边轴向廓形的倾角ωm(°)

由表1可知，当ε=5.9°时，ωm=92.634°，仅比ω小约0.05°，已相当接近。由图8可知，计算ωm所用的近似直线段放大后仍是曲线，再进一步探索ε使ωm与ω更加接近已无必要。

计算和分析表明，砂轮架垂直摆角ε选择适当时，挡边磨削廓形可以与设计廓形十分接近。

3 结论

(1)导辊挡边轴向廓形可以简化为直线并将其作为设计廓形，廓形直线对导辊轴线的倾斜角度可由(8)式计算得到。

(2)在导辊专用磨床上磨削导辊挡边，其轴向廓形根部约0.5 mm高度范围内非线性严重，其余部分近似为直线；合理选择砂轮架垂直摆角，并使砂轮越过挡边越程槽0.5 mm以上，可以使磨削廓形与设计廓形十分接近。