径向载荷作用下盾构机主轴承的有限元分析

司东宏，刘永刚，韩红彪，李建征，刘红彬

(河南科技大学 a.河南省机械设计及传动系统重点实验室;b.机电工程学院，河南 洛阳 471003)

近年来，随着我国基础建设的迅速发展，盾构施工技术作为一种先进的隧道施工方法广泛应用。盾构机作为盾构施工法中的主要施工机械，若保证在特殊环境中安全、高效的工作，必须具有高可靠性。而盾构主轴承作为盾构机的关键基础零部件，承担盾构刀盘系统与动力系统之间的回转支承任务。盾构主轴承一般为三排圆柱滚子轴承，其工作特点为：转速低、载荷大，受载情况复杂，容易产生较大的变形，从而影响盾构机械的施工安全[1-3]。因此该转盘轴承的设计中，复杂载荷作用下的静力学分析尤为重要，这对深入研究盾构主轴承的承载能力、变形、载荷分布以及预期寿命有重要意义。

目前国内、外对于盾构主轴承的力学性能分析还没有较系统的方法。由于盾构主轴承结构复杂，体积庞大，滚子数多，受载情况复杂，无法使用传统的轴承额定动、静载荷及疲劳寿命计算方法进行选型和设计。若使用解析法建立力学模型则相对复杂，误差较大；而数值计算则可克服这些缺点。有限元法是工程技术领域最常用的数值模拟法。对轴承的联合载荷分析应从单一载荷分析做起，文献[4]已对盾构主轴承在轴向力作用下的受力状态做了深入分析，因此，这里仅用有限元法分析径向力作用下轴承的静力学特性。

1 轴承结构特点

图1为盾构主轴承的结构和承载情况，第1，2排滚子承受轴向力和倾覆力矩，第3排滚子承受径向力。套圈材料为GCr15轴承钢，滚子材料为42CrMo钢。第1排滚子直径为90 mm，滚子长度为90 mm，滚子数为64粒；第2排滚子直径为50 mm，滚子长度为50 mm，滚子数为108粒；第3排滚子直径为45 mm，滚子长度为45 mm，滚子数为128粒。3排滚子沿圆周均匀分布，径向力作用于轴承内圈。此时只有第3排滚子承受径向载荷。故以下分析均是对第3排滚子进行的。

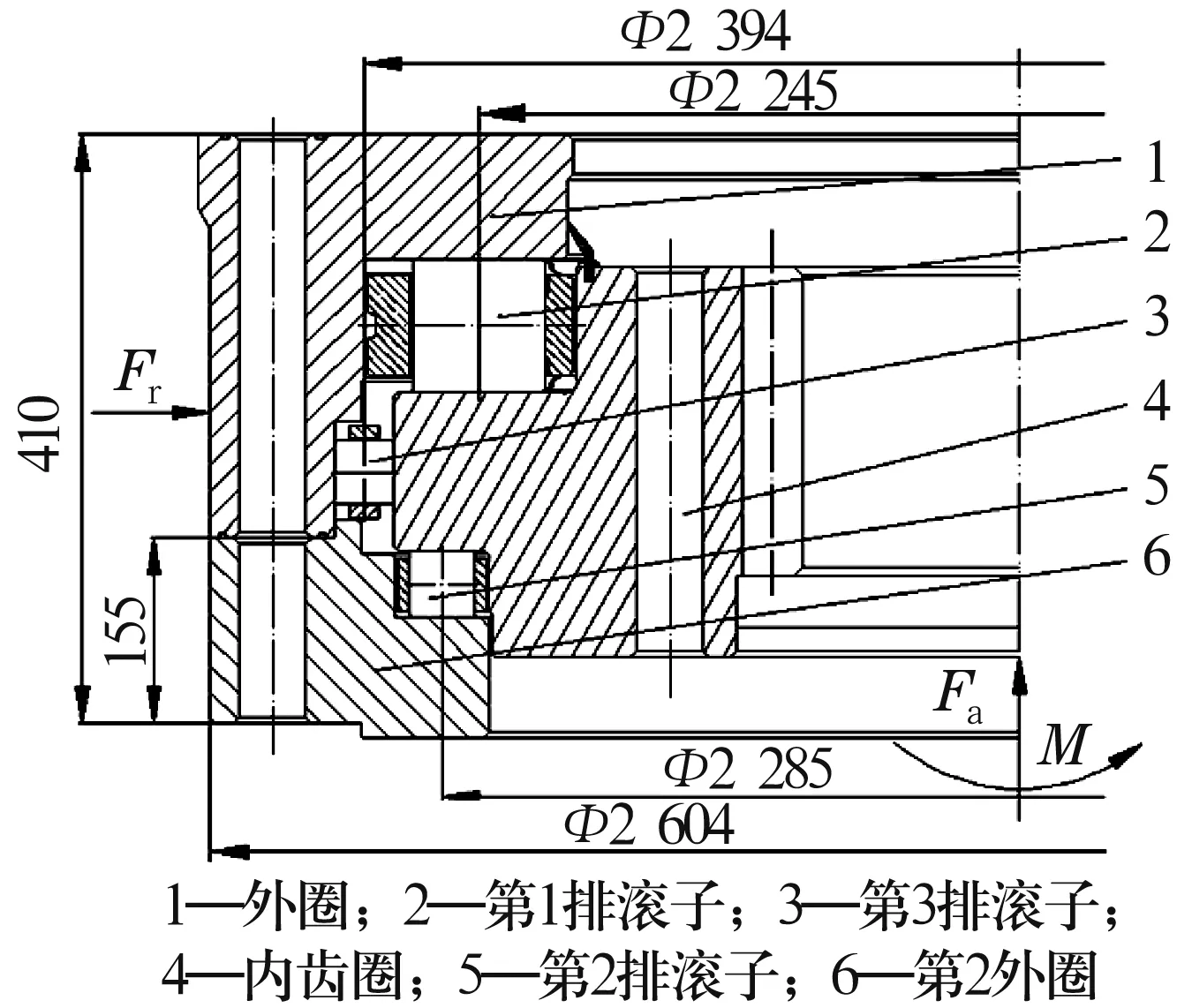
图1 轴承结构及受载状况

2 载荷分布和接触应力

在对该轴承进行分析时，为模拟最不利工况，取最大径向力Fr=2 500 kN。任意角位置ψ处滚子的接触载荷为

(1)

式中：Q0为径向载荷作用下最大滚动体载荷；δrmax为滚子的径向最大变形量；Gr为径向游隙；对于圆柱滚子轴承t=1.1。

根据Hertz接触理论，滚子接触处的最大接触应力为

(2)

式中：E为弹性模量；ν为泊松比；l为滚子的长度；∑ρ为曲率和。

从滚子轴线至内圈或外圈的弹性趋近量为

(3)

3 有限元分析

3.1 基本假设

对于尺寸较大，滚子数较多，接触部位较多的非线性分析，建立一个完整的有限元模型需要较多的内存资源，也不利于效率的提高，为了获得较高的计算精度并减小计算规模，在能够反映轴承的主要力学特性条件下，对轴承进行如下简化[4]：

(1)忽略保持架、固定螺钉、润滑和密封圈等因素对静力学分析的影响；

(2)忽略倒角、过度圆弧等部分结构尺寸的影响；

(3)忽略轴承接触分析过程中塑性变形的影响，假定轴承变形在弹性范围内；

(4)轴承内齿圈与圆周分布的8个小齿轮啮合，其载荷采用节点耦合的方式施加于内齿圈节点上；

(5)只有径向力作用时，该轴承只有第3排滚子受力，根据圣维南定理可只取该排滚子和与其接触的内、外圈部分进行分析，而不考虑其他两排滚子和与其接触的内、外圈部分。

3.2 有限元模型的建立

由于模型和所受载荷都具有对称性，为了减小计算规模，便于建立有限元模型，取轴承的一半和单个滚子来进行分析。对于轴承一半模型的分析，外加载荷取径向力Fr的一半即可。对于单个滚子分析模型的接触载荷由 (1)～(3) 式确定[5]。

采用ANSYS建模工具建立三维几何模型，所选单位为m，内、外套圈及滚子的材料均为轴承钢，其密度为7.8×103kg/m3，弹性模量为206 GPa，泊松比ν为0.3。为了获得较高的分析精度，内、外圈及滚子的网格划分均采用SOLID 45实体单元。对内、外圈采用扫略方式生成有限元网格，滚子采用映射方式生成网格，并对局部接触区域进行网格细化。接触方式采用面-面接触，接触单元和目标单元分别采用CONTA174和TARGE170单元。两个有限元模型分别如图2和图3所示。

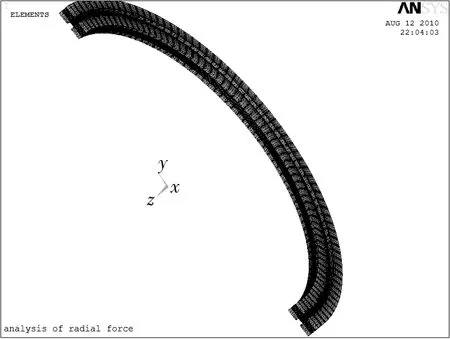
图2 二分之一轴承有限元网格模型

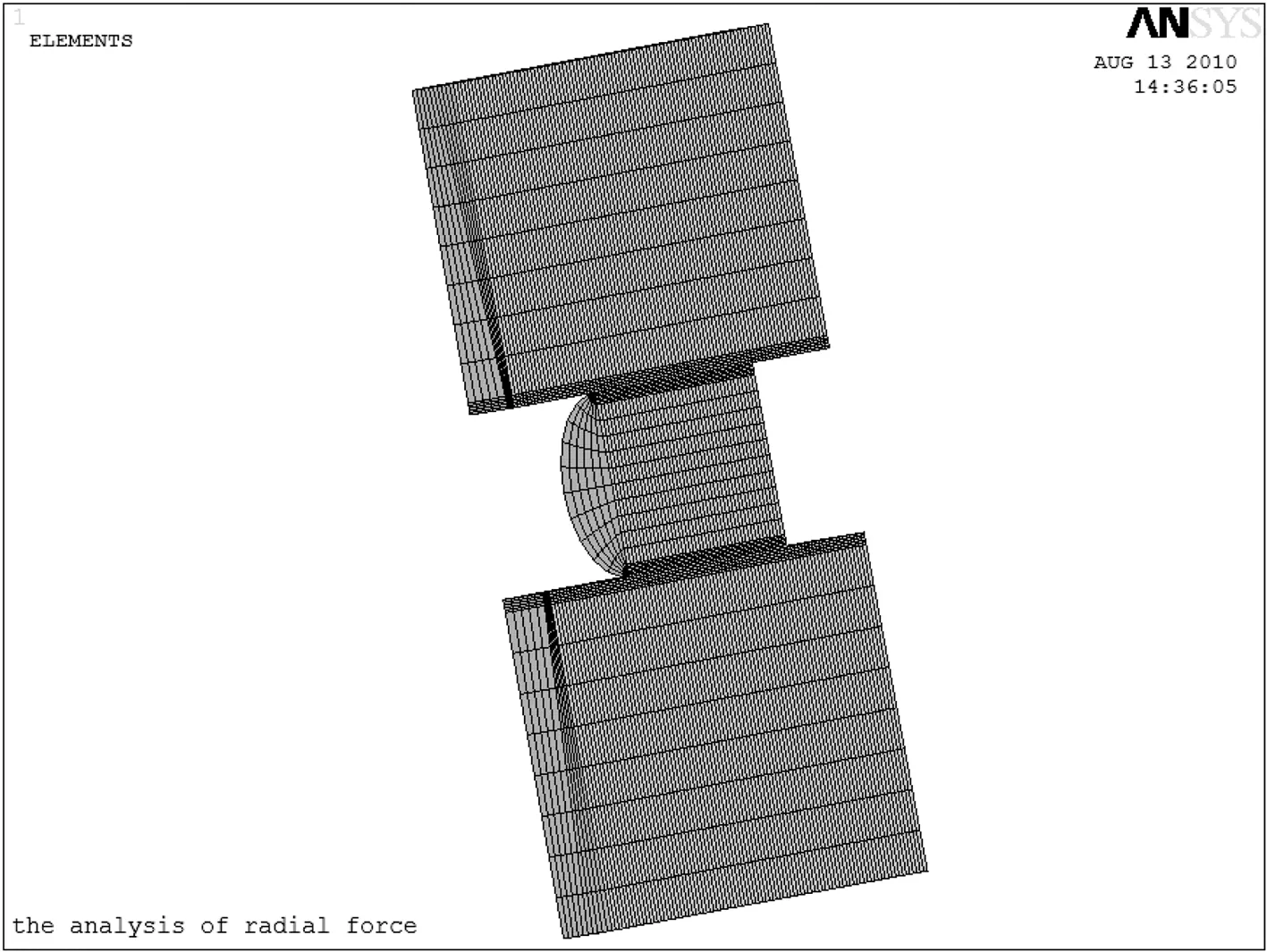
图3 单个滚子有限元网格模型

3.3 约束条件及载荷的施加

根据轴承的实际载荷，其载荷约束边界条件按如下方式施加：

(1)通过约束外圈外圆节点的所有自由度，模拟轴承外圈的固定约束；

(2)仅径向载荷作用时，其轴承的受力为对称形式，建模时取一般计算分析，故在其对称面施加对称约束边界条件；

(3)为模拟保持架的作用，在柱坐标下约束滚子与内、外圈的接触线上所有节点的圆周方向的转动自由度；

(4)耦合内圈内表面上的所有节点在x，y方向的自由度，径向力以集中力的形式施加在主节点上。

4 仿真结果分析

通过有限元计算后处理，可以得到二分之一轴承和单个滚子两种计算模型的静力学计算结果，分别如图4～图7所示。

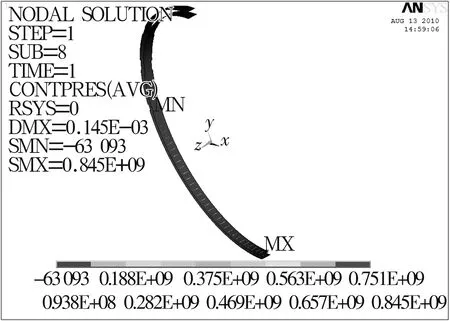
图4 套圈的接触应力云图

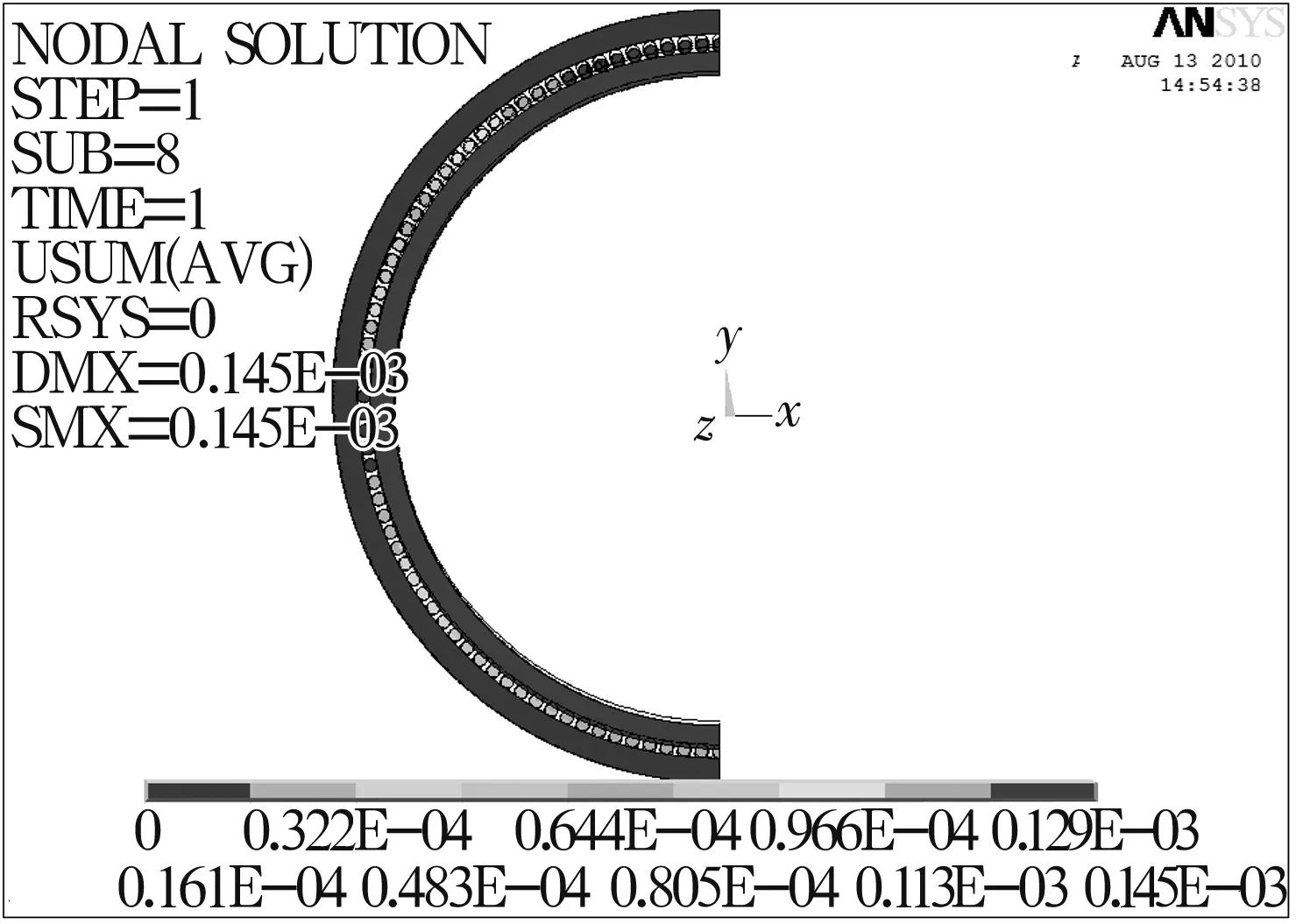
图5 套圈位移变形云图

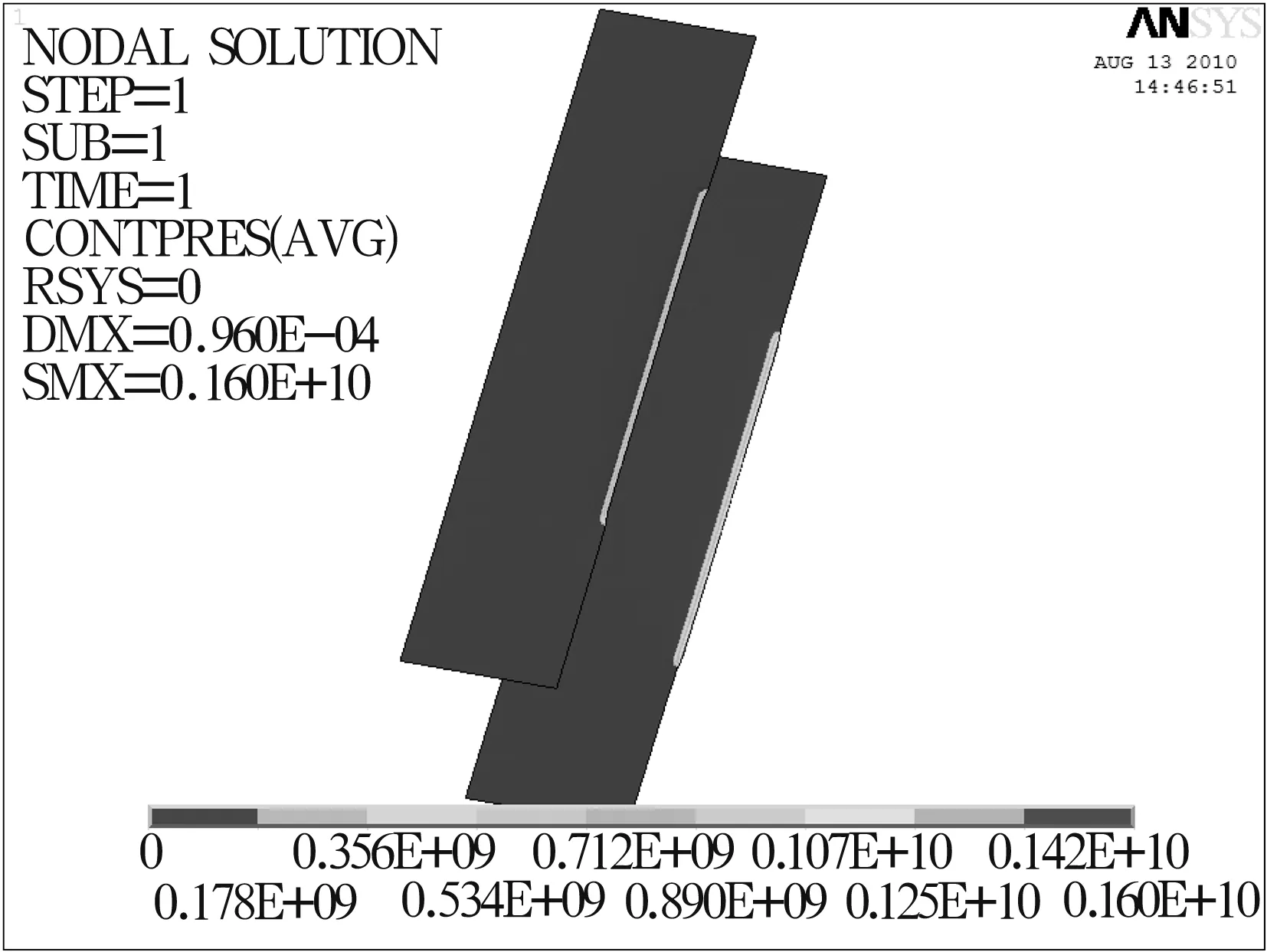
图6 单个滚子的接触应力云图

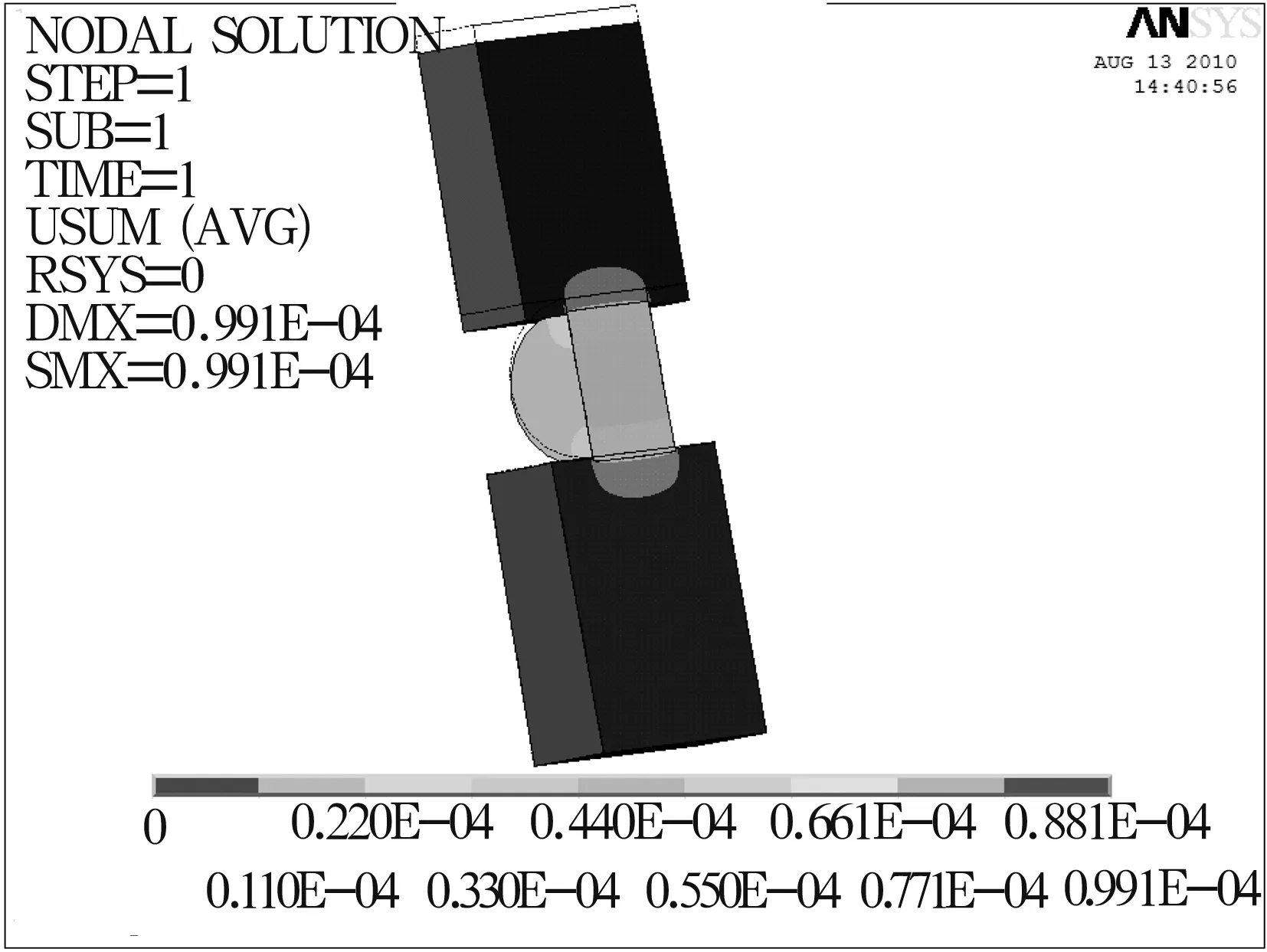
图7 单个滚子的位移变形云图

4.1 二分之一轴承模型的计算分析

由图4可以看出，在径向力作用下，上半圈的滚子不受载，而下半圈的滚子受载，且滚子与内、外圈的接触应力关于径向力作用线对称分布并向两边逐渐减小，最大接触应力在径向力作用线上的滚子与内圈接触处。上述应力的分布情况比较符合Stribeck理论，说明分析结果比较准确。

由以上分析结果可以看出径向力作用下轴承的接触应力分布，但应力分布与变形的有限元分析结果与Hertz理论计算结果相差较大。这是网格划分的质量和密度影响的结果，对于二分之一轴承模型，虽然已经在假设的前提下简化了分析模型，但考虑到计算的收敛及速度，网格划分相对稀疏。因此，在划分网格时要考虑模型的大小、计算精度及速度等，根据实际情况尽量生成较密的网格。

4.2 单个滚子的计算分析

由图6～图7可以看出径向力作用下单个滚子与内、外圈的接触应力分布情况，应力最大值出现在内圈与滚子的接触区域。除边缘外，滚子与滚道接触处的接触应力分布比较均匀。滚子与滚道接触半宽中心位置的接触应力比其他区域明显偏高，这是由于受载后滚子与滚道产生接触变形，接触应力迅速增大到最大值，产生了边缘效应[6]。边缘效应区域接触应力的大小、方向与滚道及滚子接触部分的弧度以及各自倒角形状、半径大小有关，建模一般不考虑这些，因此出现这种现象是可以理解的。

表1列出了第3排最大承载滚子的有限元计算结果和Hertz理论计算结果。从表1中可以看出，两种方法计算所得的最大接触应力和接触变形总量比较接近，但还存在一定的差异。这主要是有限元分析时轴承的简化假设、网格划分、接触算法及接触参数选择等因素造成的。

表1 有限元解和Hertz理论解的比较

5 结束语

所研究的盾构机主轴承为大尺寸、多接触和低速重载的滚动轴承。针对这一特征，建立了该轴承在径向力作用下的有限元计算模型，根据二分之一轴承模型的计算结果，可以得出轴承在径向载荷作用下滚子与内、外圈间的接触应力分布；但考虑到计算的收敛及速度，简化后的模型网格划分相对稀疏，因此计算结果不够精确，只能为定性分析提供参考。在单个滚子的有限元计算分析中，由于模型相对较小，通过对网格精细处理，得到了与经典Hertz理论相当吻合的计算结果。说明在计算资源允许的情况下，采用有限元数值模拟分析可以替代传统的Hertz理论分析，从而为后续的加载倾覆力矩和联合载荷的轴承有限元分析打下基础。