包含式半正则空间

张冠



包含式半正则空间

张冠

（五邑大学 数学与计算科学学院，广东 江门 529020）

在-Fuzzy拓扑空间中用半开集取代开集，引入了包含式半正则空间和包含式半正规空间的概念，给出了它们的一些性质，并给出了推广型Urysohn引理的证明.

-Fuzzy拓扑空间；半开集；包含式半正则空间；包含式半正规空间

1 引言及预备知识

文献[1]给出了-Fuzzy拓扑空间的包含式正则空间与包含式正规空间，本文用半开集[2]取代开集定义了两类空间，称之为包含式半正则空间与包含式半正规空间，并给出了它们的一些基本性质.

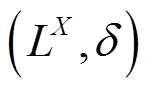
2 包含式半正则空间与包含式半正规空间

显然包含式半正则空间必然是包含式正则空间.

定理1 包含式半正则空间的开子空间是包含式半正则空间.

显然包含式半正规空间必然是包含式半正则空间.

定理2 包含式半正规空间的既开又闭的子空间是包含式半正规空间.

证明与定理1相似.

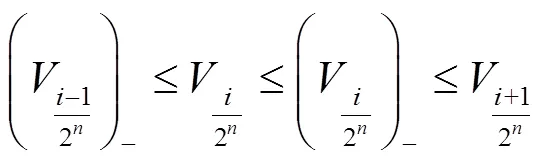
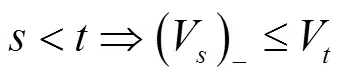
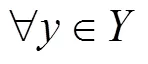
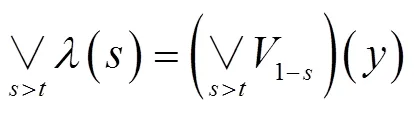
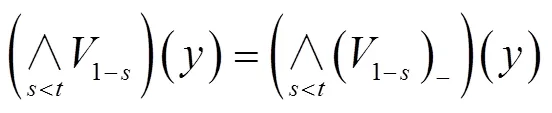
[1] 王国俊. L-Fuzzy拓扑空间论[M]. 西安：陕西师范大学出版社，1988.

[2] 白世忠，胡兰芳. 拓扑分子格中的半开元、半内部和不定序同态[J]. 徐州师范学院学报：自然科学版，1992, 10(2): 9-15.

[3] 艾为鸿. L-Fuzzy拓扑空间中的半开集与半同胚序同态[J]. 抚州师专学报，1990, 25(2): 11-18.

[4] 白世忠. 拓扑分子格上的半连续和几乎连续序同态[J]. 延安大学学报：自然科学版，1990, 13(1): 26-33.

[5] 熊金城. 点集拓扑学[M]. 北京：高等教育出版社，1978.

[6] BAI Shizhong, WANG Wanliang. Fuzzy non-continuous mappings and fuzzy pre-semi-separation axioms [J]. Fuzzy set and systems, 1998, 94: 261-268.

[7] 白世忠. 拓扑分子格的弱T~*分离公理[J]. 五邑大学学报：自然科学版，2004, 18(2): 1-4.

[责任编辑：熊玉涛]

Inclusive Semi-regular Spaces

ZHANGGuan

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

By using semi-open sets instead of open sets in-fuzzy topology spaces, two new separation axioms were introduced. Then some of their properties and the proof of generalized Urysohn lemma were given.

-fuzzy topology spaces; semi-open sets; inclusive semi-regular spaces; inclusive semi-normal spaces

1006-7302（2013）03-0012-03

O189.1

A

2013-03-21

国家自然科学基金资助项目（No.61070150）；广东省自然科学基金资助项目（S2012010008833）；广东高校科技创新项目（2012KJCX0101）；江门市科技计划项目（〔2012〕156）

张冠（1986—），男，河南周口人，在读硕士生，研究方向为格上模糊拓扑.