度量空间中满足有理不等式多个映象的公共不动点定理
2013-07-16吴志和马泽霞林锋锋陈仕洲
吴志和,马泽霞,林锋锋,陈仕洲
吴志和,马泽霞,林锋锋,陈仕洲
(韩山师范学院 数学与应用数学系,广东 潮州 521041)
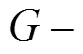
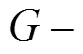
1 引言和预备知识
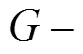
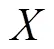
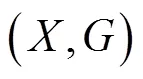
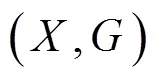
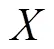
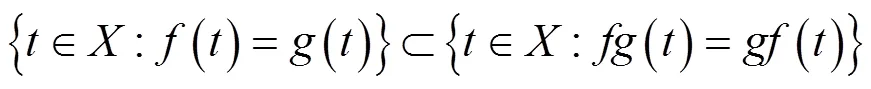
显然,可交换映象必是相容映象和次相容映象.
2 主要结果
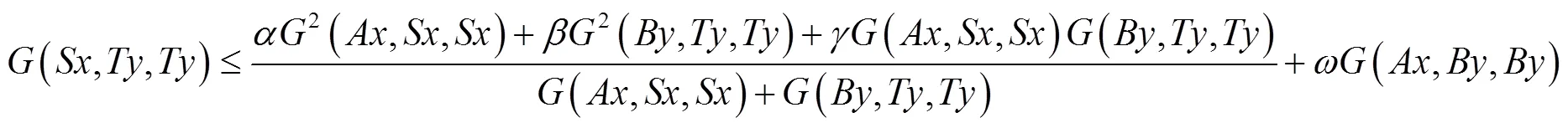
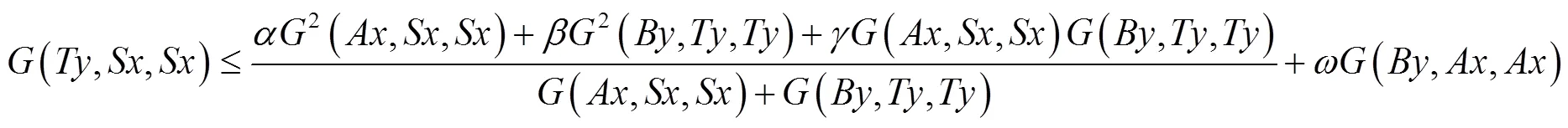
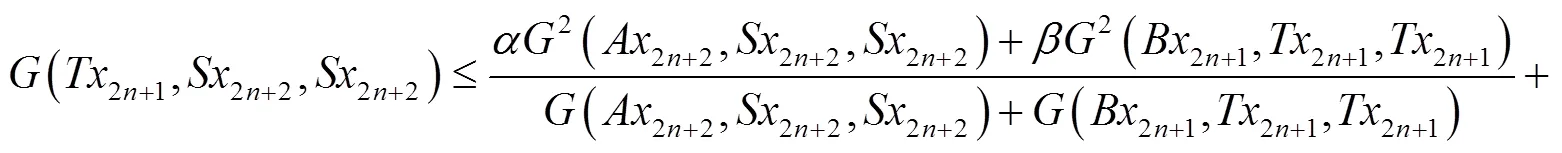
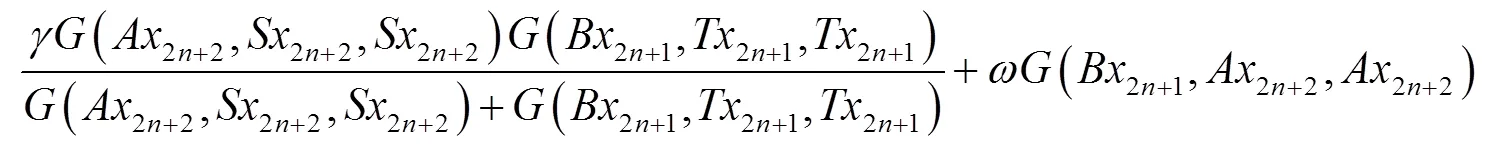
整理后得:
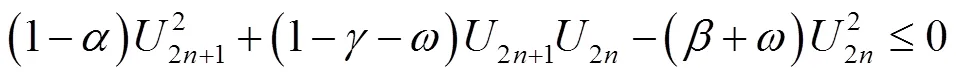
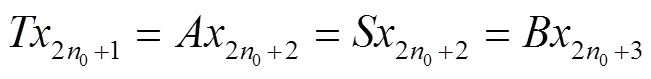
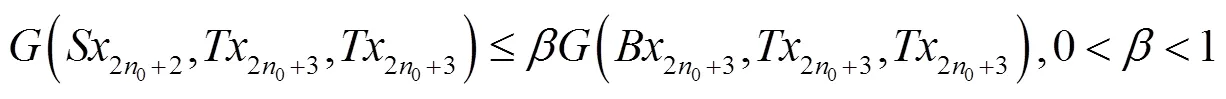
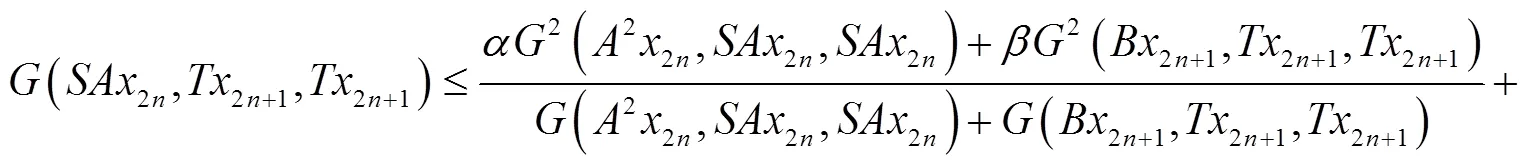
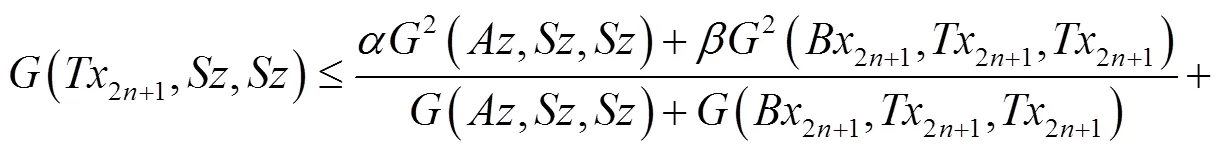
注记1 定理1是文献[2]主要结果(定理1)的推广,现举例说明定理1的真实性.
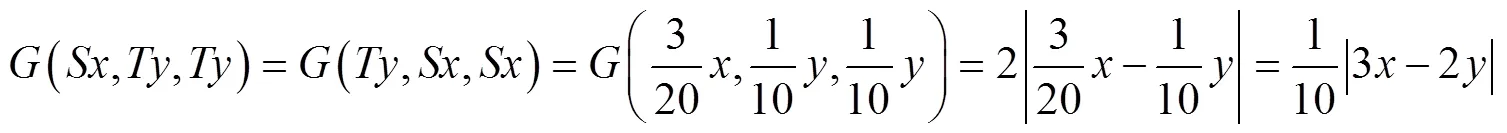
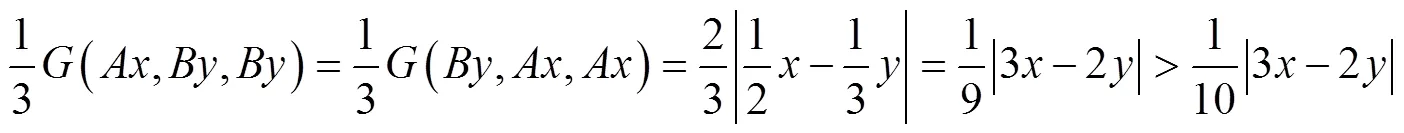
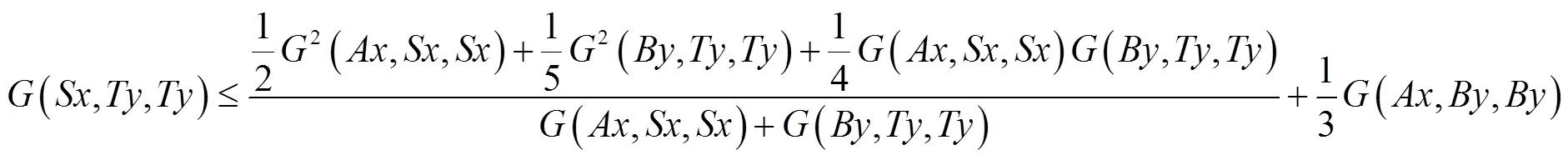
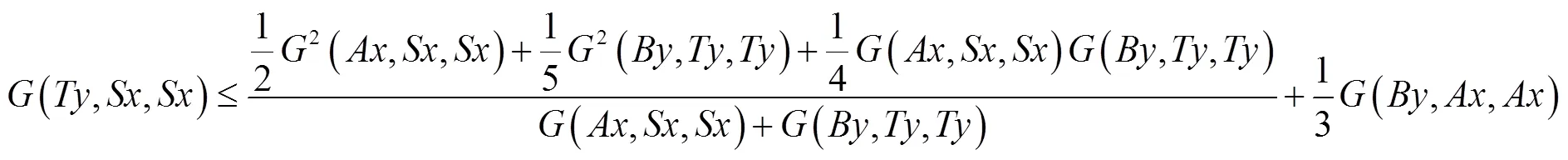
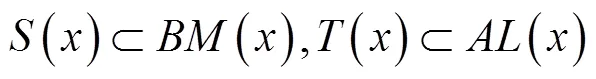
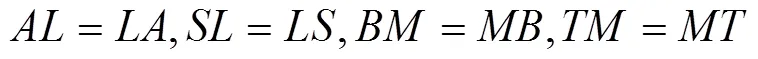
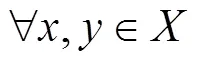

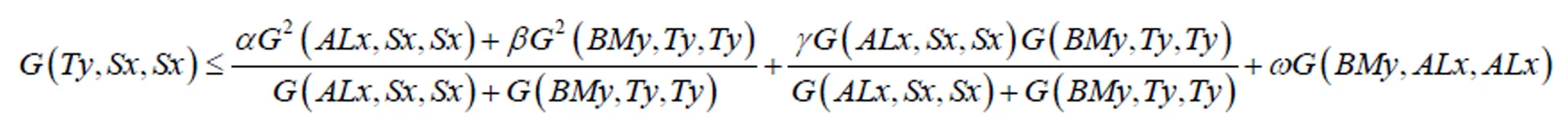
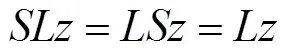
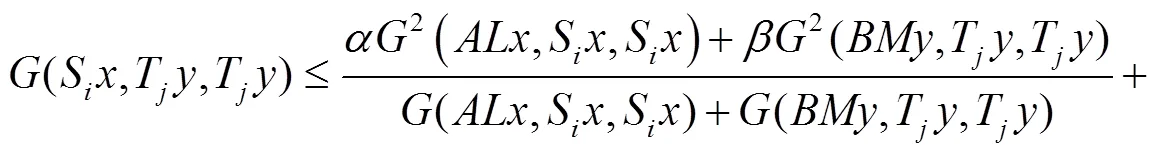
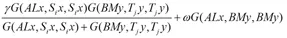
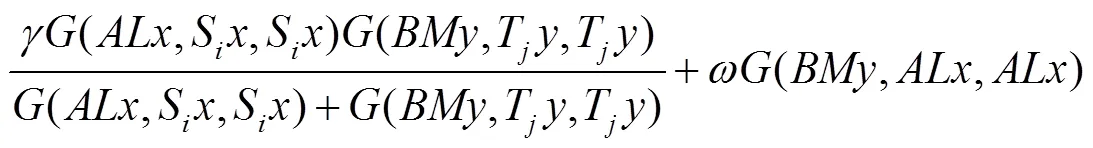
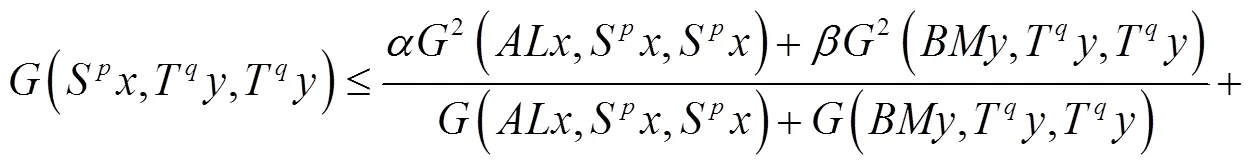
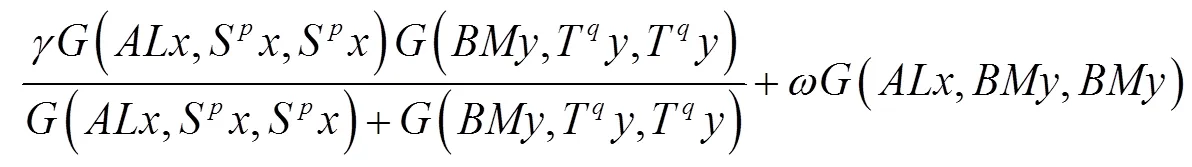
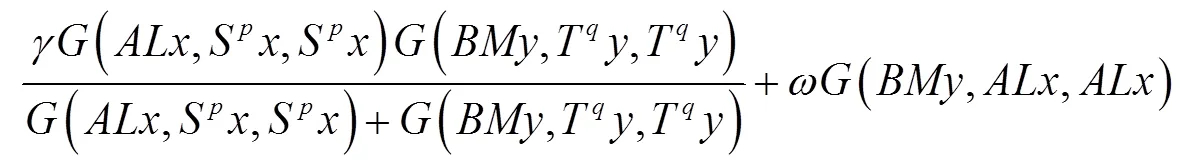
[1] MUSTAFA Z, SIMS B. A new approach to a generalized metric spaces [J]. Nonlinear Convex Anal, 2006, 7: 289-297.
[2] 李连富. 满足有理不等式四个映射的公共不动点定理[J]. 辽宁师范大学报:自然科学版,2011, 34(1): 25-29.
[4] 刘立山. (次)相容映象的公共不动点定理与广义Ishikawa迭代逼近定理[J]. 曲阜师范大学学报:自然科学版,1990, 16(2): 40-44.
[6] 张丹. 一类新的压缩条件下6个自映象的公共不动点定理[J]. 信阳师范学院学报:自然科学版,2011, 24(2): 172-177.
[7] 张石生. 不动点理论及应用[M]. 重庆:重庆出版社,1984.
[8] 朴勇杰,金月曦.-空间上满足收缩型条件的映射族的唯一公共不动点[J]. 科学系统与数学,2012, 32(5): 601-609.
[责任编辑:熊玉涛]
The Common Fixed Point Theorem for Some Mappings Satisfying a Rational Inequality in-metric Spaces
WUZhi-he, MAZe-xia, LINFeng-feng, CHENShi-zhou
(Department of Mathematics and Applied Mathematics, Hanshan Normal University, Chaozhou 521041, China)
1006-7302(2013)03-0015-06
O189;O177
A
2013-01-09
韩山师范学院大学生创新性实验(实践)项目( No.2012-71);韩山师范学院理科团队项目(LT201202).
吴志和(1991—),男,广东汕头人,在读本科生,从事泛函微分方程研究;陈仕洲,副教授,通信作者,从事泛函微分方程研究.
