连续配筋水泥混凝土路面的临界荷位＊

白 桃，黄晓明，李 昶，张德育，祝谭雍

（东南大学 交通学院，江苏 南京 210096）

从1989年中国第一条连续配筋水泥混凝土路面在盐城出现以来，连续配筋路面在国内的应用并不广泛.但随着交通重载情况的日益严重，以及道路工程全寿命费用评价的逐渐推广，连续配筋路面的应用前景亦逐步变得明朗起来.

中国目前的连续配筋水泥混凝土路面的设计计算方法[1］是简单地沿用国外以前的设计思路，然后稍加改进而成.它只考虑了温度荷载，却没有考虑车轮荷载.相较而言，美国现今的设计方法已经将车辆荷载以分级输入的方式计入路面板的疲劳损伤[2］.

正常情况下，连续配筋路面浇注完成之后，随着环境温度的改变，以及水泥水化过程的不断进行，CRCP路面板基本会在一两年内横向断裂形成一个个单独的长板条[3］.如果板条的应力计算只考虑温度应力，那么在受到板体周边约束的情况下，板条中出现温度应力最大的地方应该是板体正中间的上下表面.相应地，在环境温度的反复作用下，这些单个长板条会在正中间发生纵向断裂.而事实上，CRCP的特有破坏方式却是小板段的Punchout破坏，其发生位置一般在板条靠近路面边缘1m左右的地方，也就是轮载作用附近.这就从直观上说明了：研究CRCP的Punchout破坏不能不考虑荷载作用因素.另外，在CRCP的温度场和车轮荷载的耦合计算中，车轮荷载对板体的应力作用是不能忽视的.国内外通用的CRCP板厚设计原则是：与同等设计交通量下普通水泥混凝土板的设计厚度一致[4］，配筋只是用来控制裂缝的分布形态.配筋控制裂缝分布，裂缝分布控制板间传荷，传荷又影响荷载应力，并最终反映到CRCP的破坏上面.所以，从这个方面来讲，研究CRCP的荷载应力，在考虑车辆荷载的情况下合理配筋，以维护CRCP的良好工作性能，较好地延缓脱空和破坏极限状态的出现，是非常有必要的.

以美国的连续配筋设计方法为例，它的设计方法大多数公式都是建立在实测数据的统计分析之上，具体的计算模型也是外界所无法获取的，加上地域气候的差距，其成熟的设计方法是无法直接拿过来使用的.而现实是中国目前CRCP的有用实测数据少之又少，无法支撑计算公式的统计获取.所以，参照已有的普通水泥混凝土板设计方法，将温度应力和荷载应力分开进行理论计算，找出对应的临界荷位，然后进行叠加，不失为一个可行的方法.本文即对CRCP的临界荷位做相关研究.

1 理论背景

1.1 板间传荷定义

计算CRCP板体的荷载应力，就必须考虑横缝处板体之间的相互传力作用，这是CRCP结构计算中的难点.本文在计算中将CRCP的板体传荷作用分为两部分分别进行考虑，一部分是钢筋的传荷，另一部分是横缝断面上的混凝土嵌锁传力.

1.1.1 钢筋传荷

通常，普通接缝混凝土路面中的传力杆长度为40～60cm[5］，即埋入单块混凝土板的长度为20～30cm，而发生Punchout破坏的板长一般在30～60 cm.如果将CRCP从某一个裂缝处断开来看，左右两边埋入混凝土的钢筋都足以满足传力杆的锚固长度，可以在裂缝处将CRCP的钢筋竖向传荷类比于普通水泥混凝土路面传力杆的竖向传荷计算.其与普通混凝土板的特别之处在于CRCP的钢筋还可以提供沿路面纵向的传力作用.但本文只关心裂缝处的竖向传力，CRCP裂缝两端的混凝土板在本文中被看作是一个存在许多横向裂缝的整体板.

Friberg于1940年根据Timoshenko理论提出的传力杆力学模型[6］是混凝土路面中传力杆设计的理论基础.该模型将传力杆视为埋设在弹性介质（指传力杆周围混凝土）上的梁.钢筋的传荷刚度包括混凝土对钢筋的支撑刚度DCI和钢筋自身的剪切刚度C两部分[7］.如表1所示.

表1 钢筋传荷刚度定义Tab.1 Steel stiffness definition of load transfer

由于在实际中，很少出现钢筋拉断的情况，因此，在本文中不考虑钢筋在横缝处的应力计算.在不关注传力杆与周围混凝土接触界面的应力分布时，可假设钢筋在横缝处断开，横缝两侧埋设于混凝土内的钢筋与周围混凝土完全绑定，整体计算；而在横缝处，将钢筋端头对应的混凝土节点以弹簧连接，各方向上的弹簧刚度取钢筋传荷刚度.

1.1.2 混凝土传荷

目前，由于中国基本上所有的高速公路都使用的是半刚性基层，参照文献[1］设计方法，半刚性基层路面板嵌锁刚度为：

式中：AGG为裂缝处集料嵌锁刚度；k为地基反应模量，Pa/m；l为相对刚度半径；Jc为裂缝刚度系数；s为裂缝的抗剪能力；hpcc为CRCP板厚，m.

在有限元分析中，路面实体模型经过离散化生成单元后，混凝土板横缝处侧面的结点可分为板角结点、板边结点和板中结点.通过在对应结点设置弹簧单元，并使弹簧刚度方向与裂缝剪力方向一致，即可实现裂缝处集料嵌锁作用的传荷模拟.按照3种不同类型结点对接缝刚度的贡献面积，将裂缝的总刚度分配到每个弹簧单元上[8］.在混凝土传荷刚度计算中排除钢筋所占节点，如图1所示.

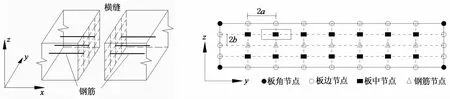
图1 节点刚度分配示意图Fig.1 Diagram of node stiffness distribution

在混凝土的刚度分配中，将板中钢筋节点排除在外，则混凝土3种位置按照结点的贡献面积进行接缝刚度分配.各类型节点的刚度贡献面积分别为：板角ab，板边2ab，板中4ab.

刚度分配面积之比为1∶2∶4，相应节点的分配刚度可以分别设置为k，2k，4k.3种位置节点数量分别为：板角4，板边2（Nh＋Nl－4），板中 （Nl－2）（Nh－3）.所以，k×4＋2k×2（Nh＋Nl－4）＋4k×（Nl－2）（Nh－3）＝qλ.整理得：

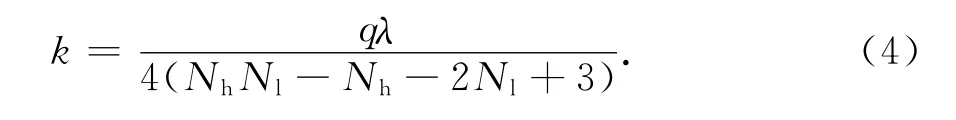
式中：q为断面传荷刚度，文中取为AGG，Pa；λ为裂缝宽度，文中取板宽；Nh为断面节点的行数；Nl为断面节点的列数.

所得的节点刚度计算公式如表2所示.

表2 节点刚度计算公式Tab.2 Calculation formula of node stiffness

1.2 轮载模拟

假设车辆的轮载均匀分布在接触面积上，文献[9］认为每个车轮与路面接触的大致形状可由1个矩形和2个半圆形组成，其接触面积Ac＝π（0.3L）2＋（0.4L）（0.6L）＝0.52L2.为方便计算，将椭圆面积等效成规则矩形面积，如图2所示.

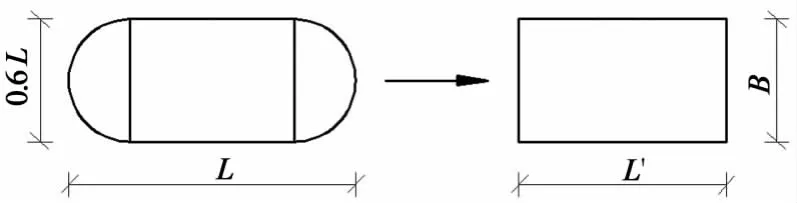
图2 轮载面积转化示意图Fig.2 Diagram of load area transformation

本文计算行车荷载采用规范规定的标准双轮轴载F＝100kN，胎压为p＝700kPa，接触面积Ac可由每个轮胎承受的荷载除以胎压求得，则

考虑到有限元计算中网格划分需求，经过试算后，将轮载区域尺寸定为0.22m×0.16m，与Ac的差值在左右，满足计算精度要求.轮载区域如图3所示.

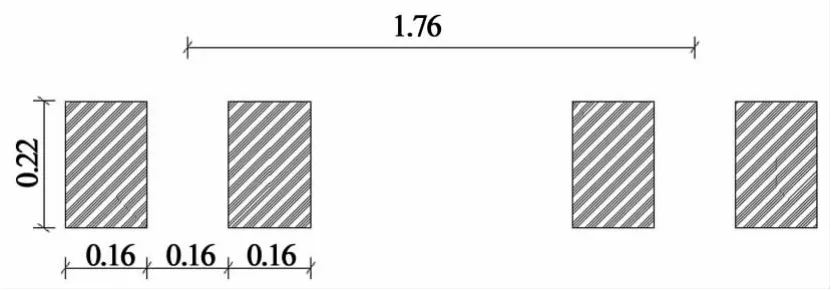
图3 轮载区域图Fig.3 Distribution of load area

2 有限元模型及其验证

2.1 基本假定及单元选用

基本假定：

1）混凝土和钢筋是各向同性、均质的弹性材料，地基选用Winkler地基.

2）钢筋和混凝土是完全理想联接的，没有滑移，使用植入方式处理.

3）路面选用三板系统，如图4所示，中间板段长度根据需要为0.5～3m，其中两边板端部除竖直方向外，其他方向都约束住.事实上三板系统中两边板跟中间板段长度差不多，但是，本文计算主要是为了降低边界约束对裂缝传力的影响，所以，将边板看作一个（带裂缝的）整体来进行计算.

4）路面板单元采用二十节点六面体二次完全积分单元，钢筋采用二节点杆单元.

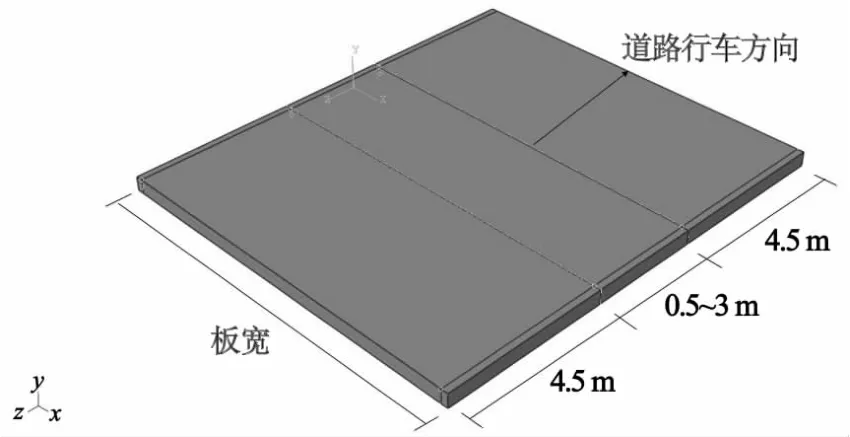
图4 CRCP有限元模型计算示意图Fig.4 FEM model of CRCP

单元选用：

如图1所示，在3种混凝土节点上设置弹簧单元，赋予z轴向弹簧刚度为各节点的节点刚度（表2）.在钢筋节点上设置3个方向上的弹簧单元，其中，y和z向分别为钢筋切向刚度，x向为纵向刚度，见表1.

2.2 轮载分布

实际工程中，多车道混凝土路面大多选择分幅施工，通过减小单幅混凝土板块的宽度以减小温度效应.同时，单车道混凝土路面比较少见.因此，本文选择双车道混凝土路面进行研究.为计算连续配筋路面的临界荷位，本文选取如5所示的8个荷载位置分别进行荷载应力计算.

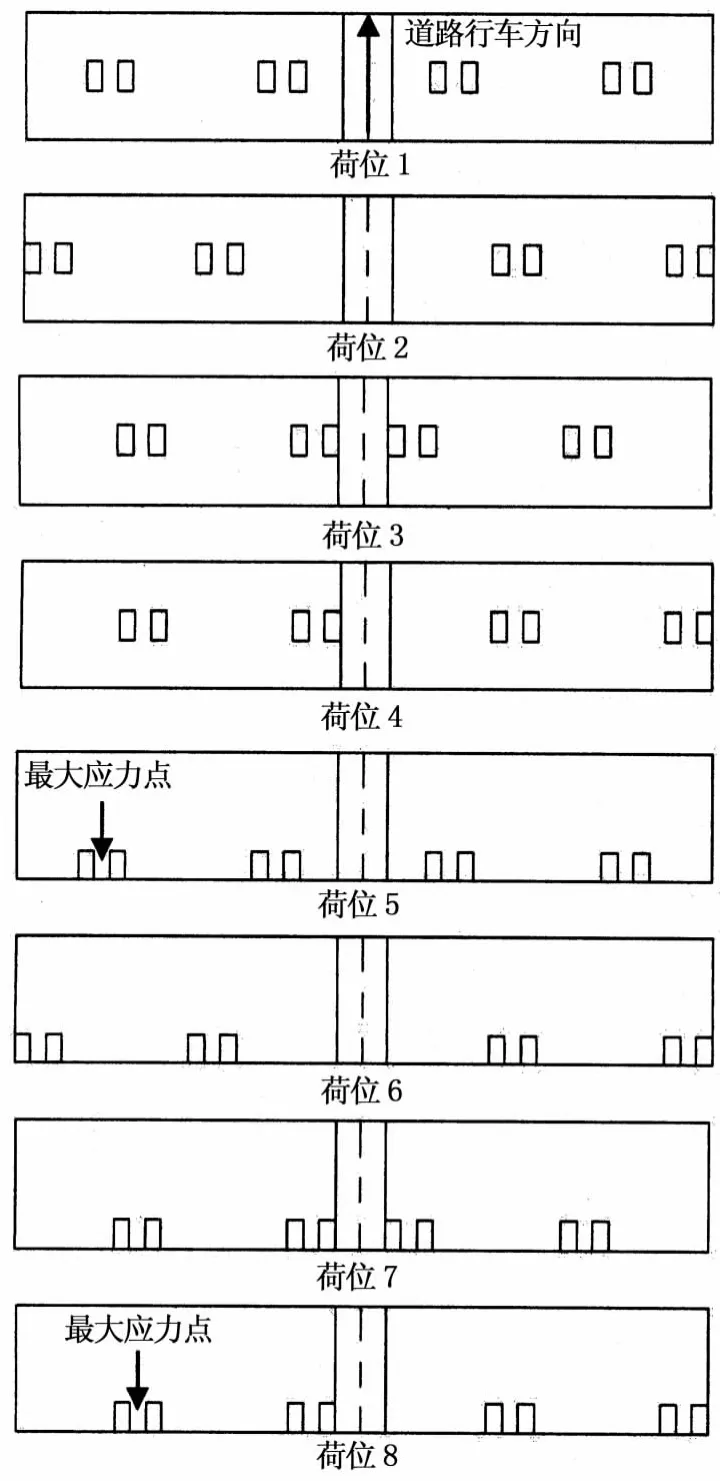
图5 中间板块荷载位置示意图Fig.5 Load position of middle plate

其中，荷位1～4是轮载作用于中间板块正中间的情况，对应于荷位1～4，荷位5～8位于横缝边缘.图中各板块正中间的双竖线表示两车之间的安全距离.考虑到荷载划分的方便，本文取此双线之间的距离为0.45m.

2.3 模型验证

由于连续配筋路面在道路纵向上是连续的，因此当图4中中间板块受到轮载作用时，其变形会传导到相邻两侧板上.也就是说，中间板块的变形对两侧板存在一定长度的影响区间，此区间长度即决定本计算中两边板的长度取值.当边板中存在横向裂缝时，边板的整体刚度削弱，区间长度会有所调整，但是本文只关心取定长度下边板边缘区间段受力为零.由于参数变化，每一种参数组合对应一个区间长度.但是很明显，当中间板块长度和横向裂缝宽度越小时，边板受影响的区域越大.取中间板段宽0.5 m，裂缝宽度0.1mm，板厚0.24m，板中配筋，钢筋间距0.16m，钢筋直径18mm，边板宽分别取1.5，2.5和4.5m进行计算，材料参数见表3[10］.按图5中的荷位1进行边板影响区域计算.

表3 材料参数表Tab.3 Material parameters for calculation

经计算，两边板在板长方向上出现的最大应力点的连线垂直于横向裂缝，并经过外侧车轮轮迹中心点.对左边板，以裂缝处为应力取值点初始位置，在垂直裂缝方向上间断取点，取值点连线经过应力最大点，各点的应力点如图6所示.

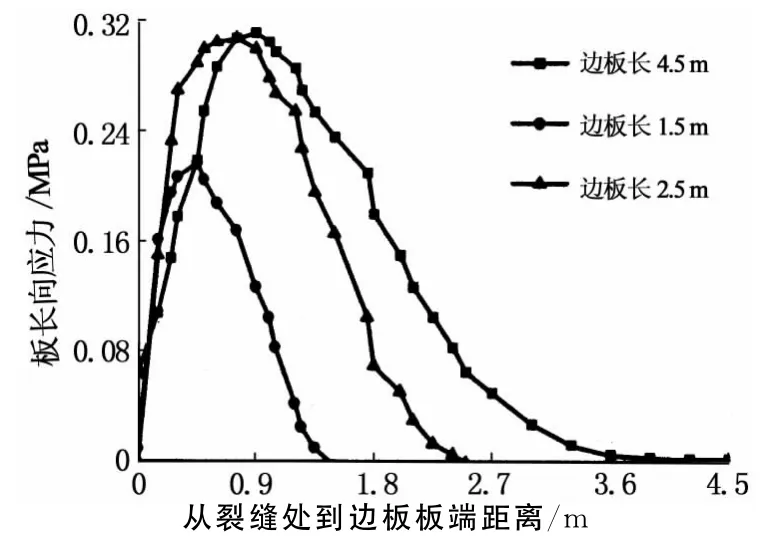
图6 边板在板长方向上的拉应力分布Fig.6 Tensile stress distribution along the length direction in the side plate

由图6可知，当边板长分别为1.5和2.5m时，在接近边板端部处应力迅速递减为零，虽然符合模型边界条件，但是这一现象也表明中间板块荷载对边板端部处存在一定影响，也即边板长度取值不够.也就是说，如果此时限定边板端部位移为零，则边界条件必定会对整个系统中的应力产生影响，从而影响计算结果的精确性.而当板长为4.5m时，板长向应力在4m处即趋于零，并在4～4.5m内板体应力都为零，表明荷载对边板的影响位置最大在4 m左右，本文选取4.5m，满足要求.

3 临界荷位计算

当边板长度取定之后，也就确定了本次计算所需的所有参数.按图5中的8种荷载位置对三板块系统进行应力计算，确定中间板块的最大板宽向拉应力的荷载位置，即为临界荷位.在取定边板长度为4.5m情况下，变化中间板块的长度，分别为0.5，1，2和3m，其他参数同2.3节.计算所得结果如表4所示.从表4可以看出，当板长较大（≥1.0m）时，与板宽向应力相比，板长向应力为主要应力.而当板长较小（0.5m）时，板宽向应力成为主要应力.同实际情况相对应，在CRCP横向裂缝不断产生、板长不断减小的过程中，板长向拉应力逐渐减小，从而使板宽向应力成为小板段CRCP中的控制应力.这符合CRCP寿命周期中的行为方式：即当板块板长较大时，板体在荷载和温度的共同作用下在长度方向上不断开裂，当板体长度减小为一定（0.3～0.6m）时，CRCP将不再在板长向上发生断裂，反而会在荷载作用下出现板宽向的小板条断裂，即punchout破坏.

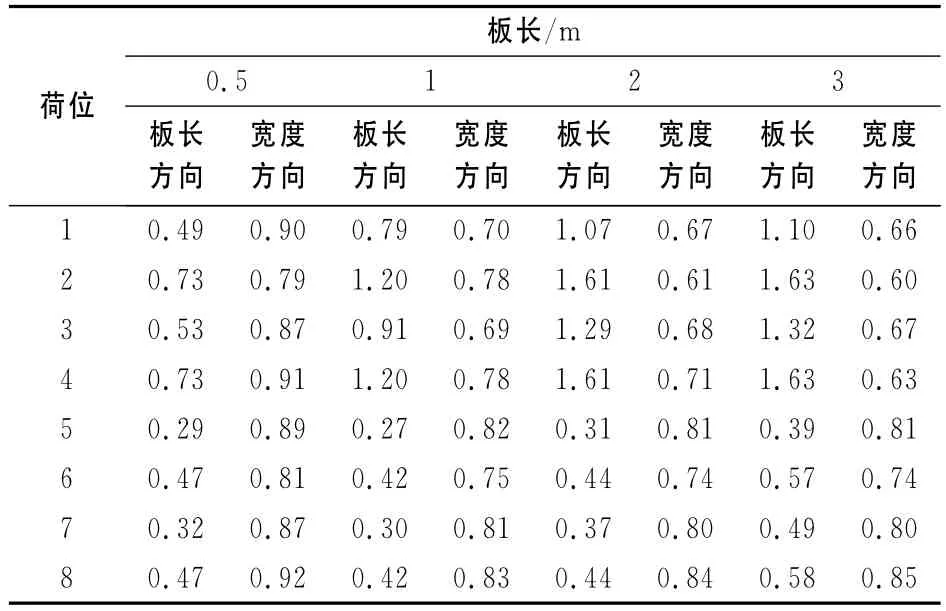
表4 不同荷位和板长下中间板段的最大拉应力Tab.4 The maximum stress of middle plate when plate length and load position change MPa

总体来说，板宽向应力随板长变化改变不大.但是，不同板长情况下，荷位8在板宽向的应力在与其他荷位的比较中总是最大的，也就是说，荷位8为所求的临界荷位.此时，板宽向最大拉应力位于左车道外侧车轮板底轮迹中心处（见图5），距离路面板边缘为1.43m.

当中间板条较小时（0.5～1.0m），从表4中可以看出，荷位5相较于荷位6和荷位7，与荷位8非常接近.荷位5情况下，板宽向最大应力也是出现于左车道外侧车轮板底轮迹中心处（见图5），距离路面板边缘0.95m.荷位8和荷位5情况下，最大板宽向应力的发生位置与实际中punchout的发生位置（距路面板纵向边缘1.0～2.0m）能很好地吻合.考虑行车道划分，正常行驶的轮迹分布是以荷位1和荷位5为中心的类似正态分布.在混凝土疲劳计算中，需考虑荷载位置在路面横断面上的概率分布，对各位置处的损伤进行累计计算，而推荐荷位8作为路面承载力检验的核算位置.

4 结 论

以三板系统模拟连续配筋水泥混凝土路面，计算获得了路面的临界荷位.CRCP裂缝处钢筋和混凝土的传荷刚度计算公式的确定，为模拟CRCP荷载应力计算提供了关键参数.在此基础上，大量计算结果表明：

1）三板系统中，当边板长度大于4m时，边界条件将不对应力计算产生影响.本文中边板长度4.5m满足计算要求.

2）连续配筋路面中，板宽向最大应力位置发生于本文荷位8情况下左车道外侧车轮板底的轮迹中心处.

3）连续配筋混凝土路面的临界荷位为图5中的荷位8，在混凝土疲劳计算中，需考虑荷载位置在路面横断面上的概率分布，对各位置处的损伤进行累计计算，而推荐荷位8作为路面承载力检验的核算位置.

[1]JTG D40—2002 公路水泥混凝土路面设计规范[S］.北京：人民交通出版社，2003：92－94.JTG D40—2002 Design specification of cement concrete pavement design for highway[S］.Beijing：China Communications Press，2003：92－94.（In Chinese）

[2]ARA，Inc，ERES Division.Mechanistic－empirical design guide 2002，appendix LL：punchouts in continuously reinforced concrete pavement [S］.Illinois，USA：505West University Avenue，Champaign，2003.

[3]白桃，黄晓明，李昶，等.连续配筋水泥混凝土路面温缩应力简化公式研究[J］.湖南大学学报：自然科学版，2011，38（6）：1－5.BAI Tao，HUANG Xiao－ming，LI Chang，etal.Simplified formula research on temperature contraction stress of continuously reinforced concrete pavement[J］.Journal of Hunan University：Natural Sciences，2011，38（6）：1－5.（In Chinese）

[4]邓学均，陈荣生.刚性路面设计[M］.2版.北京：人民交通出版社，2005：425－427.DENG Xue－jun，CHEN Rong－sheng.Rigid pavement design[M］.2nd ed.Beijing：China Communications Press，2005：425－427.（In Chinese）

[5]邓学钧.路基路面工程[M］.3版.北京：人民交通出版社，2006：423－425.DENG Xue－jun.Subgrade and pavement engineering[M］.3rd ed.Beijing：China Communications Press，2006：423－425.（In Chinese）

[6]FRIBERG B F.Design of dowels in transverse joints of concrete pavements[J］.Transactions of the American Society of Civil Engineers，1940，105：1076－1095.

[7]唐益民.连续配筋水泥混凝土路面荷载应力分析[D］.南京：东南大学交通学院，1996：12－13.TANG Yi－min.Research on the load stress of continuously reinforced concrete pavement[D］.Nanjing：School of Transportation，Southeast University，1996：12－13.（In Chinese）

[8]周正峰，凌建明，袁捷.机场水泥混凝土道面接缝传荷能力分析[J］.土木工程学报，2009，42（9）：112－118.ZHOU Zheng－feng，LING Jian－ming，YUAN Jie.3－D finite element analysis of the load transfer efficiency of joints of airport rigid pavement[J］.China Civil Engineering Journal，2009，42（9）：112－118.（In Chinese）

[9]王斌，杨军.移动荷载作用下连续配筋混凝土路面三维有限元分析[J］.东南大学学报：自然科学版，2008，38（5）：850－855.WANG Bin，YANG Jun.Effects of vehicle dynamic loading on CRCP by 3Dfinite element method[J］.Journal of Southeast University：Natural Sciences，2008，38（5）：850－855.（In Chinese）

[10］白桃.连续配筋水泥混凝土温度应力研究[D］.南京：东南大学交通学院，2010：14.BAI Tao.Research on the thermal stress of continuously reinforced concrete pavement[D］.Nanjing：School of Transportation，Southeast University，2010：14.（In Chinese）