600MW循环流化床锅炉水冷壁设置防磨梁后炉内气固流场的数值研究

夏云飞， 程乐鸣， 张俊春， 王勤辉， 方梦祥

（浙江大学 热能工程研究所，能源清洁利用国家重点实验室，杭州310027）

大容量、高参数化是循环流化床锅炉的发展方向之一［1］，但循环流化床锅炉受热面存在的磨损问题影响其运行安全性、稳定性和综合效益.

在循环流化床锅炉炉膛内，固体颗粒沿水冷壁表面向下加速流动，长期冲刷水冷壁表面会造成水冷壁管磨损.水冷壁的磨损速率与其表面颗粒流速度的3～3.5次方及贴壁颗粒浓度成正比［2］.

在炉膛水冷壁边壁上设置多阶式防磨梁可以有效地破坏高浓度贴壁颗粒下降流，减小颗粒的下降速度，从而抑制水冷壁受热面磨损［3－5］.该技术已开始应用于300MW循环流化床锅炉.西安热工研究院［3］和浙江大学［4］等已提出不同结构形式的防磨梁（见图1）.

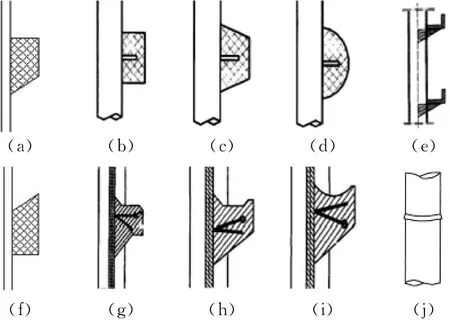
图1 各种形式的防磨梁Fig.1 Structural diagram of various anti－wear beams

在循环流化床锅炉水冷壁壁面设置防磨梁后，防磨梁对炉内气固流场（特别是固体颗粒沿壁面的流动）产生影响，从而影响循环流化床锅炉炉内的传热、燃烧和产物生成等特性，如一些循环流化床锅炉安装防磨梁后出现床温升高、排烟温度上升或减温水量增加等现象.

在600MW循环流化床锅炉研发中，了解和掌握循环流化床锅炉炉膛壁面设置防磨梁对炉内流场的影响是锅炉设计和安全运行的基础.600MW循环流化床锅炉炉膛面积较大，实炉测试困难，模化试验存在缩小效应问题，采用数值模拟计算来了解其流场和变化规律是一个比较理想的选择.

在大型循环流化床锅炉炉内流场数值模拟的文献中，大多数研究是针对空炉甚至其二维模型、局部区域模型或冷态试验台模型进行模拟［6－10］的.针对水冷壁壁面设置防磨梁后对炉内气固流场影响的数值研究较少.

笔者以600MW裤衩腿循环流化床锅炉为研究对象，利用Fluent软件，运用结合颗粒动力学的双流体模型对加装梯形防磨梁前、后炉内气固流体动力特性进行数值模拟，分析防磨梁结构对炉内气固流场和壁面磨损的影响.

1 模型及结果处理方法

1.1 几何模型和网格划分

基于某600MW裤衩腿循环流化床锅炉，建立计算几何模型，宽度沿y轴方向（左墙为负方向，右墙为正方向），宽度W 为15.03m；深度沿x轴方向（后墙为负方向，前墙为正方向），深度D为27.9m；高度沿z轴方向，高度H 为55m.二次风风口分上、下2层布置在炉膛下部裤衩腿壁面上，6个分离器沿炉膛宽度方向布置，对应的返料口环绕分布于裤衩腿外围四周.梯形防磨梁设置在炉膛稀相区四周水冷壁上（见图2），呈多阶阶梯式布置，其中防磨梁向炉内凸起的高度S＝50mm.

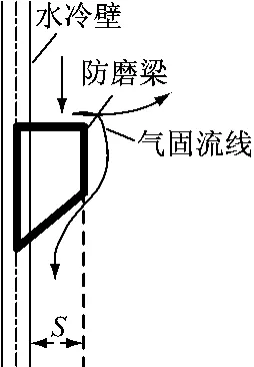
图2 梯形防磨梁示意图Fig.2 Schematic diagram of a trapezoidal anti－wear beam

炉膛几何模型和网格划分如图3所示.在网格划分中，加装防磨梁前、后炉膛中间稀相区和炉膛出口均采用六面体结构化网格，稀相区壁面区域网格局部加密；裤衩腿区域为四面体非结构化网格，返料管和二次风管区域采用楔形网格.此外，对防磨梁附近区域进行了网格局部加密，同时采用渐变网格以保证主体网格与加密网格的过渡性和解的正确性.

1.2 计算模型及参数

目前，循环流化床锅炉炉内气固两相流动特性数值模拟的数学模型主要有用欧拉方法描述的连续介质模型和用拉格朗日方法描述的颗粒轨道群模型［6，11］.其中，计算量相对较小、结合颗粒动力学［12－13］且基于欧拉方法的双流体模型应用较广泛［6，10－11］.

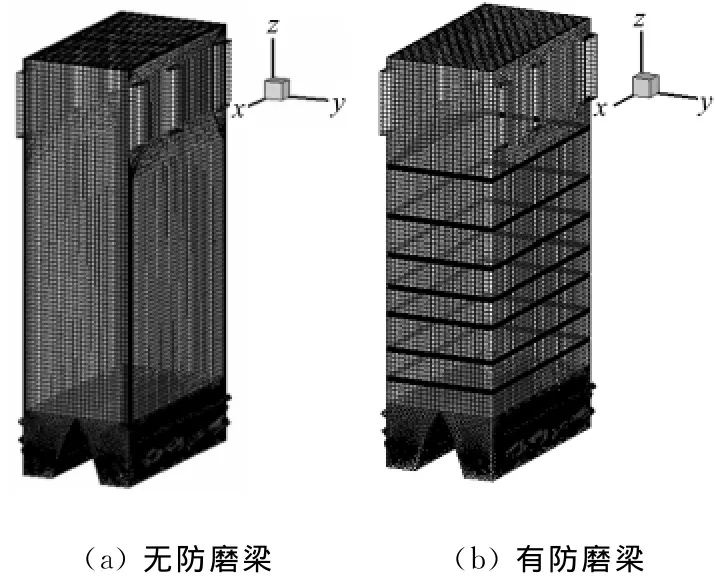
图3 炉膛几何模型和网格划分Fig.3 Geometric model and grid division of the furnace

计算中设置气固两相流动为非稳态流动，气相和固相湍流模型分别采用RNG k－ε模型和Per Phase k－ε模型；采用控制容积法离散控制方程，流体压力－速度耦合基于Simple算法；采用在气固两相流模拟中应用广泛的Gidaspow曳力模型［10，14］描述 气 固 两 相 间 的 动 量 传 递［8，10］，相 比 于 其 他 模型［11，15］，该曳力模型能够较好地得到炉膛气固流场径向分布和炉膛贴壁区域气固流动情况，且计算量相对较小；气相壁面条件设置为无滑移边界条件，固相为部分滑移边界条件；一次风风口和二次风风口采用速度入口边界条件，炉膛出口为压力出口边界条件.

在模拟计算中，炉膛表观气速为5.4m／s，二次风风率为0.54；采用的颗粒粒径为0.4mm，设置其密度为2 400kg／m3.气固两相从炉膛出口运行至返料口的过程（即循环流化床锅炉外循环）通过UDF实现［11］，每个炉膛出口对应2个返料口.

模拟中假定炉内温度呈890℃单一分布.由于二次风进入炉膛后经过轴向膨胀和径向扩散过程，计算中基于二次风与炉膛中心风的动量比相等原则，采用二次风风口矫形理论对二次风风口尺寸进行修正［11］.

1.3 数值模拟结果的处理方法

在外循环返料口处设立监视器，记录整个非稳态过程返料口的返料质量流率qm，以返料质量流率是否稳定作为炉内流场是否稳定的判定条件.如图4所示，在模拟计算时间t＝70s后，返料质量流率基本稳定，对t＝70s后约30s时间内每隔0.1s时的流场样本进行时均处理，得到流场分布.

为得到防磨梁对距离壁面不同位置处贴壁颗粒下降流的影响，采用所取数据点的位置和相应近壁面的水平距离与S之比Ln（n＝1，2，3）进行分析，它表示所取数据点在炉膛中与壁面及防磨梁的相对径向位置.表1给出了Ln值和对应的数据点在炉膛中的径向位置.

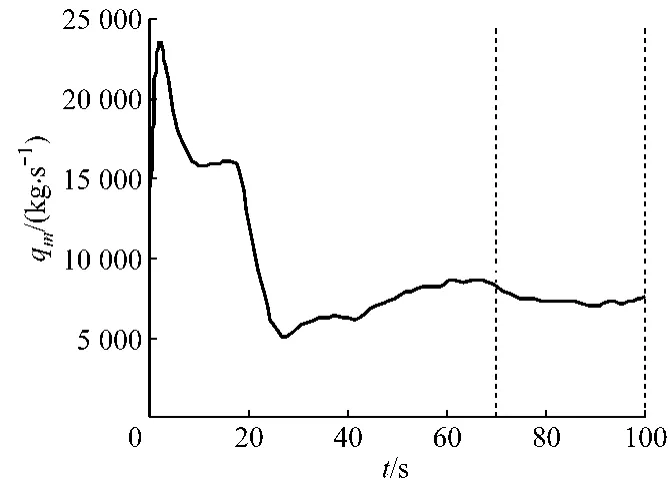
图4 返料口固相质量流率随时间的变化Fig.4 Variation of solids mass flow at feed back inlet with time

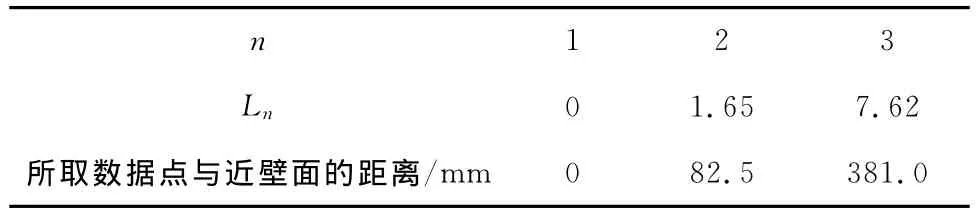
表1 Ln值Tab.1 Lnvalues

2 结果及分析

2.1 防磨梁对炉内颗粒平均质量浓度及轴向速度分布的影响

图5为加装防磨梁前、后炉膛颗粒平均质量浓度ρs沿轴向的无因次分布.总体上，炉内颗粒质量浓度呈上稀下密的典型分布.加装防磨梁后，炉膛颗粒平均质量浓度在稀相区下部区域（图5中h／H＝0.38左右以下区域）略有减小，而在稀相区上部区域（图5中h／H＝0.38左右以上区域）略有增大.这是因为阶梯式防磨梁的存在使得沿壁面下滑部分颗粒遇到防磨梁的阻挡后折向炉膛中心区域，这些颗粒被上升气流再次托起扩散（见图6），使得更多的颗粒留在炉膛稀相区中上部区域；相反，原先贴壁下降流颗粒减少，炉膛稀相区下部区域颗粒平均质量浓度有所减小.此外，加装防磨梁后炉膛稀相区中上部中心区域颗粒体积分数比无防磨梁时大，如图7所示，加装防磨梁后在z＝30m和z＝40m截面上炉膛中心区域颗粒的体积分数有所增大，而在z＝10m截面上颗粒的体积分数则减小.

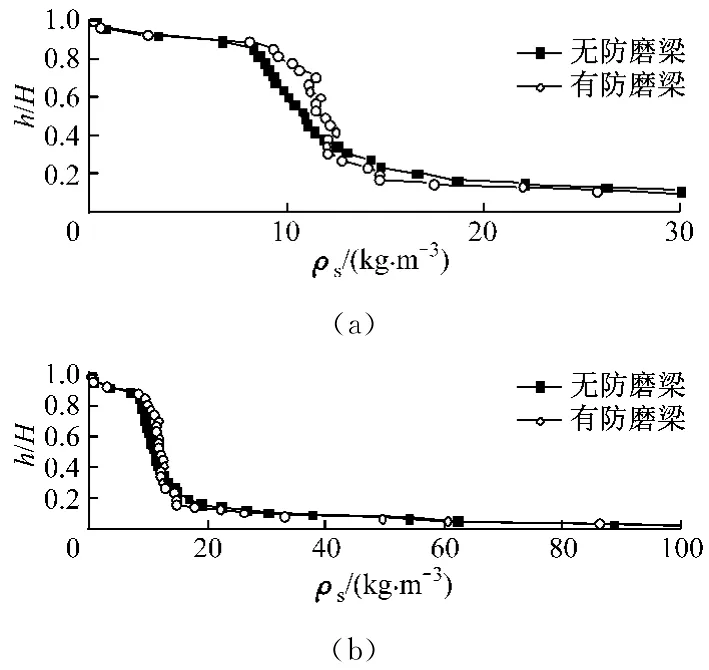
图5 炉膛颗粒平均质量浓度沿轴向的分布Fig.5 Axial profiles of average solids mass concentration in the furnace

图6 防磨梁对贴壁颗粒流体积分数的影响Fig.6 Effect of anti－wear beams on volume fraction of granular flow adherent to the wall

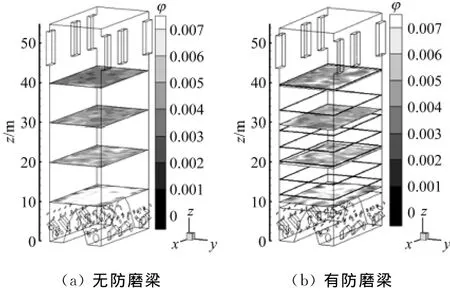
图7 炉膛不同高度截面上颗粒的体积分数分布Fig.7 Distribution of solids volume fraction at different furnace heights

图8为加装防磨梁前、后炉膛横截面颗粒轴向速度υs沿炉膛宽度方向的无因次分布.由于稀相区下部气固流动受到裤衩腿结构的影响，颗粒轴向速度呈“M”型分布，如在h／H＝0.18截面上，中心区域颗粒速度小于两侧颗粒速度，CHENG Leming等［16］针对带六分离器裤衩腿循环流化床锅炉炉内气固流动特性的试验研究也得到了类似的结论.但防磨梁的存在改变了气固局部流场，减弱了流场“M”型分布的趋势.此外，由于受到左右墙分离器入口的影响，在相同高度处对炉膛中心区域的抽吸作用弱于靠近炉膛出口两侧区域，从而使得这种结构一直延伸到稀相区的上部，如有防磨梁炉膛h／H＝0.73截面所示.

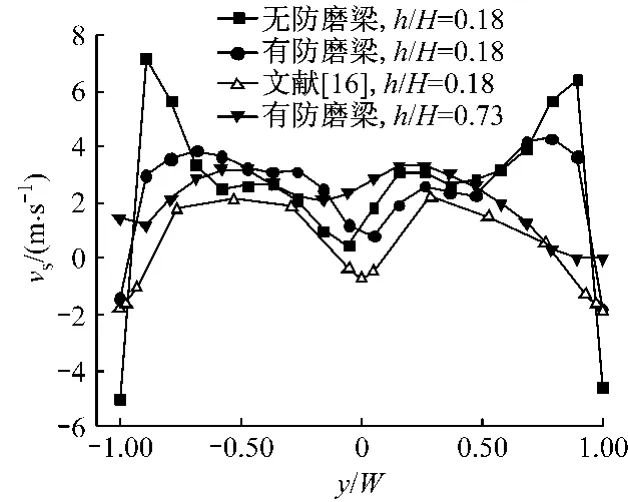
图8 颗粒轴向速度沿炉膛宽度方向的分布Fig.8 Profiles of solids axial velocity along furnace width

2.2 防磨梁对贴壁区域颗粒轴向速度分布的影响

图9为加装防磨梁前、后炉膛壁面颗粒的轴向速度分布.由图9可以看出，炉膛贴壁区域存在颗粒下降流；加装防磨梁后，炉膛前墙与右墙水冷壁表面颗粒轴向速度的分布规律相似.

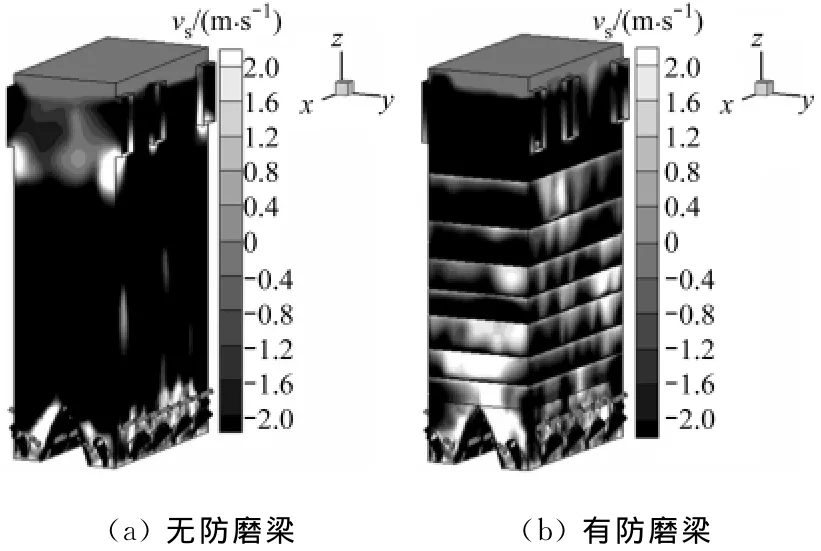
图9 炉膛壁面颗粒轴向速度分布Fig.9 Profiles of solids axial velocity on furnace wall

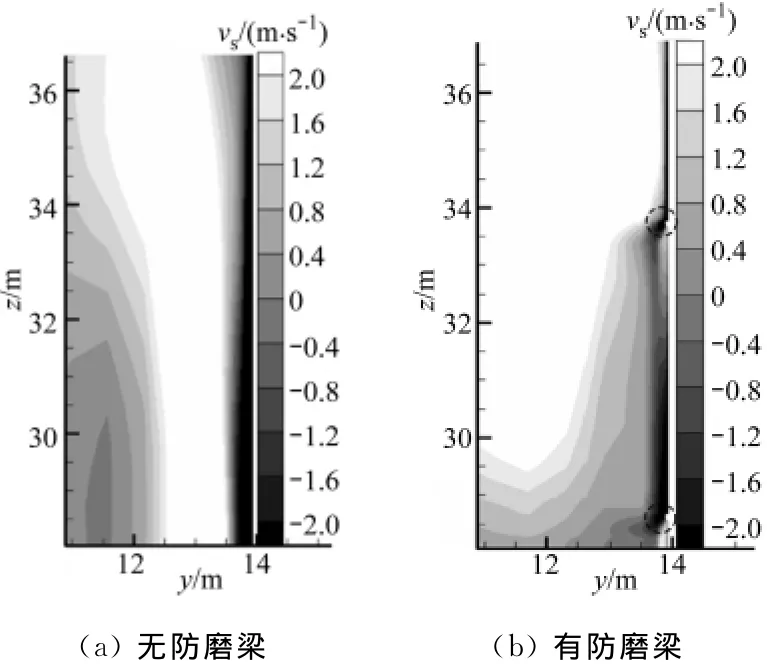
图10 防磨梁局部区域颗粒轴向速度分布Fig.10 Profiles of solids axial velocity in local region around anti－wear beams

图10为防磨梁局部区域颗粒的轴向速度分布，圈出部分为防磨梁区域.由图10可以看出，防磨梁的存在破坏了贴壁颗粒下降流，使得贴壁颗粒下降速度和回流区厚度减小，减弱了颗粒速度项对壁面的磨损作用；在2个防磨梁间段，贴壁颗粒流下降速度和回流区厚度逐渐增大，在接近下层防磨梁时均达到最大值；S范围内的贴壁颗粒下降流在遇到防磨梁之后，下降流速度骤减，部分颗粒因防磨梁的阻挡而折向炉膛中心，被上升气流托起冲散，如图11所示.

由图11可知，遇到防磨梁而折向炉膛中心的部分颗粒被上行的流化风托起一段距离后再沿壁面下落，如此反复循环形成涡流，可能会导致该部位磨损相对加剧.随着炉膛高度的减小，壁面区域颗粒质量浓度和粒度均增大，涡流造成的磨损将会加剧.

图11 防磨梁局部区域颗粒速度矢量分布Fig.11 Distribution of solids velocity vector in local region around anti－wear beams

图12为加装防磨梁前、后炉膛壁面颗粒轴向速度沿高度方向的分布，正速度颗粒流不属于贴壁下降流.L3区域因距离炉膛壁面相对较远，防磨梁对流场的影响很小；随着与炉膛壁面距离的减小，未加装防磨梁炉膛贴壁颗粒下降流速度增大，下降流区域增大，防磨梁对颗粒下降流的影响也逐渐增强，规律性更加明显并呈现出相似性.

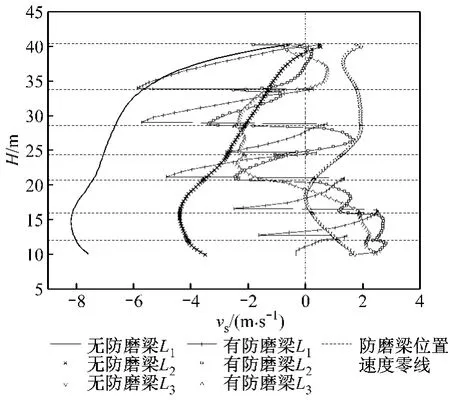
图12 炉膛壁面颗粒轴向速度沿高度方向的分布Fig.12 Profiles of solids axial velocity on the wall along furnace height

图12中L1区域数据表示紧贴水冷壁表面网格区域内颗粒流轴向速度的分布情况，其中颗粒轴向速度为负值的颗粒流是贴壁下降流的一部分.由图12可以看出，沿水冷壁表面，贴壁颗粒下降流在遇到防磨梁后速度骤减至0，甚至反弹向上运动，并在防磨梁及其以下一段区域无下降流存在；当贴壁颗粒下降流在防磨梁下沿的某个位置（速度零点）重新形成时，速度很小，壁面摩擦阻力较小，速度加速度比无防磨梁时有所增大，贴壁颗粒下降流加速下滑直至遇到下一层防磨梁；当壁面加装防磨梁后，此区域的贴壁颗粒下降流速度总体减小幅度较大，且随着高度的减小和防磨梁层数的增加，下降速度减小幅度增大，最大下降速度平均为－2m／s左右，有效减小了对水冷壁壁面的磨损.此外，由于防磨梁阻挡了部分贴壁颗粒下降流，防磨梁下一段区域出现少量颗粒低压区，炉膛中心区域颗粒可能会补充进入此区域并向上流动（见图11），所以此区域内出现了少量的颗粒上升流现象，改变了传统的贴壁下降流状态.

图13为加装防磨梁前、后炉内不同高度壁面附近颗粒轴向速度分布，其中Z1为H＝29m（由上往下第三层防磨梁上沿）高度的数据，Z2为H＝12.8 m（第七层防磨梁上沿）高度的数据，与壁面距离由小到大依次为L1、L2和L3.根据L1数据，并结合图12可知，加装防磨梁炉膛贴壁颗粒下降流越往下，其总体速度越小，对原本磨损严重的稀相区中下部、过渡区水冷壁管的磨损改善尤为明显，这与无防磨梁炉膛贴壁颗粒下降流沿轴向越往下速度越大、对水冷壁管磨损越大的变化趋势相反；根据L2和L3数据，随着与壁面距离的增大，贴壁颗粒下降流受防磨梁的影响逐渐变得无规律.

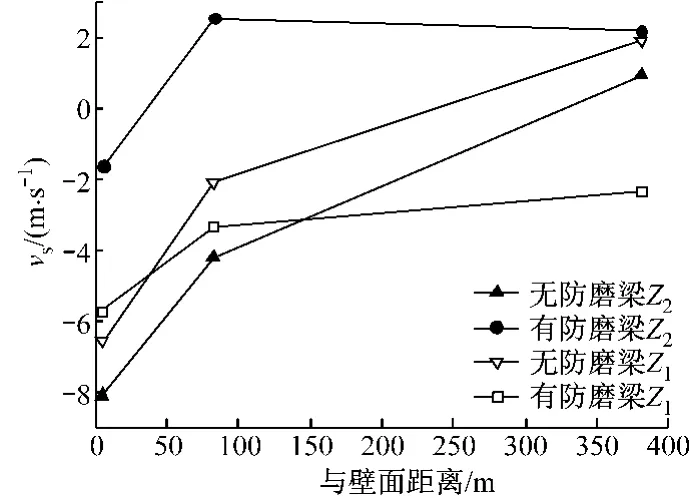
图13 炉膛不同高度壁面颗粒轴向速度分布Fig.13 Profiles of solids axial velocity on furnace wall at different heights

2.3 防磨梁对贴壁区域颗粒浓度分布的影响

图14为防磨梁局部区域颗粒体积分数的分布，可以看出在炉膛壁面加装防磨梁后，边壁颗粒回流高浓度区受到破坏，贴壁颗粒流在未遇到防磨梁前，颗粒体积分数逐渐增大，但遇到防磨梁后，部分颗粒流被防磨梁阻挡转向炉膛中心进行扩散；贴壁颗粒体积分数在防磨梁上沿及周围部分区域达到最大，在防磨梁下沿最小，当贴壁颗粒下降流在防磨梁下沿某个位置重新形成后，颗粒沿炉膛边壁又重新汇聚，贴壁颗粒体积分数在下一防磨梁上沿达到最大.

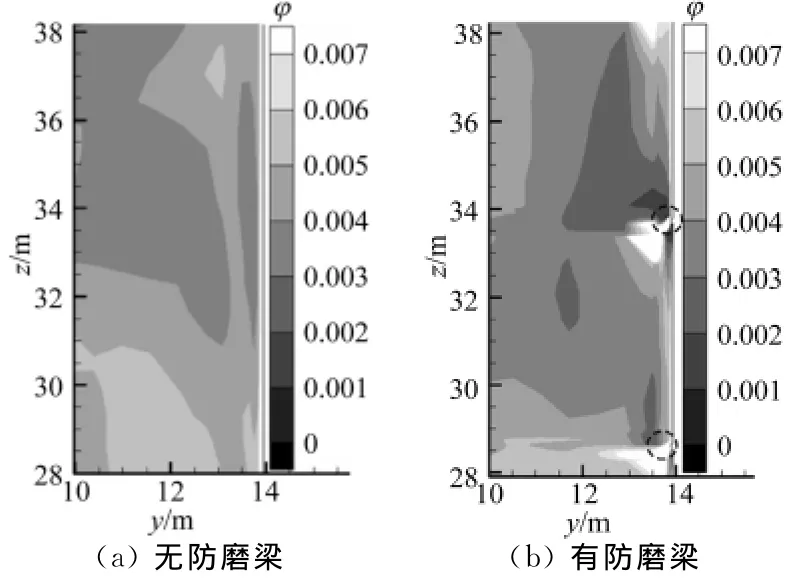
图14 防磨梁局部区域颗粒体积分数的分布Fig.14 Profiles of solids volume fraction in local region around anti－wear beams

图15为加装防磨梁前、后炉膛L1区域颗粒质量浓度ρs1沿轴向的分布.由图15可以看出，加装防磨梁后，沿水冷壁表面，当贴壁颗粒下降流在防磨梁下沿某个位置（图12中L1区域数据速度零点位置）形成并向下流动时，颗粒质量浓度较小，外围颗粒加入此区域贴壁颗粒下降流的趋势增加，2层防磨梁之间贴壁回流颗粒质量浓度的增加速度大于无防磨梁时此区间颗粒质量浓度的增加速度.此区域中不同2层防磨梁之间颗粒质量浓度分布存在差别，如最下层防磨梁，由于其炉膛高度较低，颗粒质量浓度受密相区影响较大，质量浓度较大，颗粒呈反向聚集趋势；最上层与第二层防磨梁之间，贴壁颗粒下降流仅受防磨梁阻挡一次，总体壁面颗粒质量浓度比其以下几层防磨梁之间区域的颗粒质量浓度大.

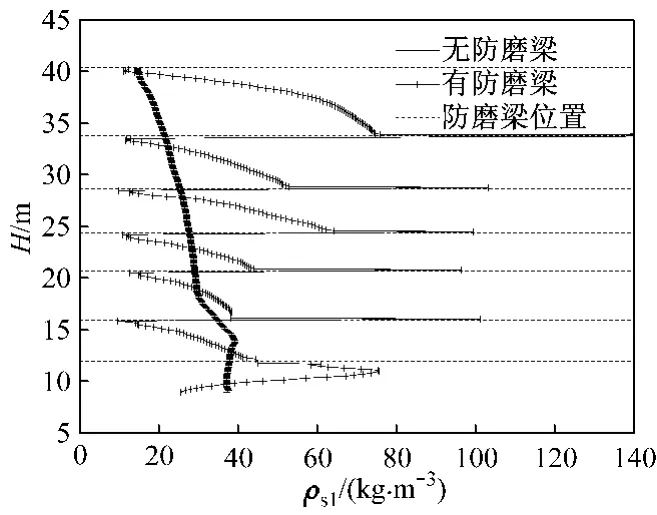
图15 炉膛L1区域颗粒质量浓度的轴向分布Fig.15 Axial profiles of solids mass concentration in the region of L1

2.4 防磨梁的防磨效果

研究表明，壁面磨损量与烟气速度的n次方成正比，与壁面附近固相的质量浓度成正比［2］.岑可法等［2］给出了不同烟气速度下n的取值范围.由于颗粒的粒径相对较大，表观气速较低，因此本文计算中n取3.

加装防磨梁前、后炉膛水冷壁磨损量的变化主要取决于水冷壁表面颗粒流速度和质量浓度的变化.忽略其他因素对壁面磨损的影响，根据加装防磨梁前、后炉膛水冷壁相对磨损量E0［10］（E0＝ρs1×υs1）数值的变化对防磨梁防磨效果进行定性分析.

图16为加装防磨梁前、后炉膛水冷壁相对磨损量沿轴向的分布.由图16可以看出，防磨梁的存在总体上减轻了贴壁颗粒流对水冷壁壁面的磨损，降低的磨损量约为无防磨梁炉膛水冷壁磨损量的30%；每2层防磨梁之间，由上向下磨损量逐渐增大，邻近上一层防磨梁下沿区域的磨损量最小，靠近下一层防磨梁区域的磨损量最大；同时防磨梁结构导致部分颗粒流转向，甚至产生涡流，使得防磨梁附近壁面区域的磨损量大于远离防磨梁壁面区域的磨损量，所以加装防磨梁后，防磨梁附近壁面区域的磨损应引起重视.

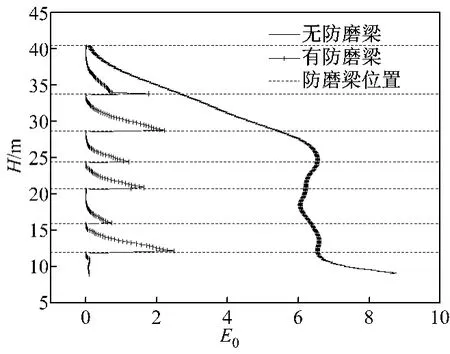
图16 炉膛水冷壁相对磨损量的轴向分布Fig.16 Axial profiles of wear values of furnace wall

3 结 论

（1）对于“裤衩腿”炉膛结构，设置防磨梁后炉膛颗粒轴向速度呈“M”型分布，与无防磨梁时的轴向速度分布类似，但防磨梁的存在削弱了颗粒轴向速度呈“M”型分布的趋势.

（2）防磨梁破坏了高浓度贴壁颗粒下降流，使其下降速度减小，回流区厚度减小；受防磨梁阻挡折向炉膛中心区域的颗粒使得炉膛颗粒平均质量浓度在稀相区下部区域略有减小，上部区域略有增大.

（3）多阶防磨梁将贴壁颗粒下降流分隔成相似的几段颗粒速度和质量浓度增加的下降流，贴壁颗粒下降流在防磨梁下沿某个位置时的速度和质量浓度最小，至下一层防磨梁上沿时速度和质量浓度均达到最大值.2层防磨梁之间特别是S范围内，贴壁回流颗粒的质量浓度和下降速度增加速度均大于无防磨梁时此区间回流颗粒的质量浓度和下降速度的增加速度.

（4）加装防磨梁后，贴壁颗粒流对壁面的磨损量总体上有所减小，但防磨梁附近壁面区域的磨损量相对较大.

［1］程乐鸣，周星龙，郑成航，等.大型循环流化床锅炉的发展［J］.动力工程，2008，28（6）：817－826.CHENG Leming，ZHOU Xinglong，ZHENG Chenghang，et al.Development of large－scale circulating fluidized bed boiler［J］.Journal of Power Engineering，2008，28（6）：817－826.

［2］岑可法，倪明江，骆仲泱，等.循环流化床锅炉理论设计与运行［M］.北京：中国电力出版社，1997：676－686.

［3］西安热工研究院有限公司.一种带有防磨装置的循环流化床锅炉炉膛：中国，200520118121.2［P］.2007－01－03.

［4］浙江大学.循环流化床反应器内壁面的防磨结构：中国，200820083290.0［P］.2009－01－28.

［5］蒋敏华，肖平.大型循环流化床锅炉技术［M］.北京：中国电力出版社，2009：307－318.

［6］姬广勤.循环流化床锅炉内气固两相流动特性的试验与数值研究［D］.青岛：中国石油大学（华东），2009.

［7］CABEZAS G L，MILIOLI F E.Numerical study on the influence of various physical parameters over the gas－solid two－phase flow in the 2Driser of a circulating fluidized bed［J］.Powder Technology，2003，132（2／3）：216－225.

［8］HARTGE E U，RATSCHOW L，WISCHNEWSKI R，et al.CFD－simulation of a circulating fluidized bed riser［J］.Particuology，2009，7（4）：283－296.

［9］郭贞，郭庆杰，刘宝勇，等.循环流化床底部区域流动特性的数值模拟［J］.中国粉体技术，2008，14（6）：13－17.GUO Zhen，GUO Qingjie，LIU Baoyong，et al.Simulation of flow characteristics in bottom zone of a circulating fluidized bed［J］.China Powder Science and Technology，2008，14（6）：13－17.

［10］马志刚.无烟煤循环流化床内流动、燃烧与磨损的研究［D］.杭州：浙江大学，2007.

［11］王超.600MW超临界CFB锅炉炉膛气固流动特性的数值模拟研究［D］.杭州：浙江大学，2011.

［12］CHAPMAN S，COWING T G.非均匀气体的数学理论［M］.北京：科学出版社，1985.

［13］DING J，GIDASPOW D.A bubbling fluidization model using kinetic theory of granular flow［J］.AIChE Journal，1990，36（4）：523－538.

［14］郑成航，程乐鸣，周星龙，等.300MW单炉膛循环流化床锅炉二次风射程的数值模拟［J］.动力工程，2009，29（9）：801－805.ZHENG Chenghang，CHENG Leming，ZHOU Xinglong，et al.Numerical simulation of secondary air penetration depth in a 300MW single－furnace circulating fluidized bed boiler［J］.Journal of Power Engineering，2009，29（9）：801－805.

［15］SHAH M T，UTIKAR R P，TADE M O，et al.Hydrodynamics of an FCC riser using energy minimization multiscale drag model［J］.Chemical Engineering Journal，2011，168（2）：812－821.

［16］CHENG Leming，ZHOU Xinglong，WANG Chao，et al.Gas－solid hydrodynamics in a CFB with 6cyclones and a pant－leg［C］／／10th International Conference on Circulating Fluidized Beds and Fluidization Technology.Oregon，USA：［s.n.］，2011：497－504.