易变质商品的二级库存模型的合作策略

李斌，潘秀娟，范昌胜

（1.陕西广播电视大学工程管理部，西安 710068；2.天津工业大学理学院，天津 300387）

易变质商品的二级库存模型的合作策略

李斌1，潘秀娟2，范昌胜1

（1.陕西广播电视大学工程管理部，西安 710068；2.天津工业大学理学院，天津 300387）

针对易变质商品的两级库存系统中的库存控制策略问题，在需求率、变质率确定的情况下，建立了供应商和销售商的易变质商品的库存控制数学模型.假设该模型中易变质商品的寿命分布函数服从指数分布，将供应商和销售商之间的二级库存的合作问题转化为一个生产商自给自足的生产问题.最后通过算例及函数图像，验证了模型的正确性和求解算法的有效性.通过与传统方法对比，得出了最优的库存控制参数，避免了销售商库存水平呈指数增长.

寿命分布函数；易变质；库存水平；控制参数

经济订货批量（economic order quantity，EOQ）是固定订货批量模型的一种，可以用来确定企业一次订货（外购或自制）的数量.当企业按照经济订货EOQ来订货时，可实现订货成本和储存成本之和最小化.易变质商品的库存系统是现实中最常见的一种供应链管理系统，例如食品的变质、挥发性物质的挥发等.研究易变质商品的两级库存系统，对提高易变质商品服务水平和降低整个供应链系统总成本，都具有重要的意义.关于易变质物品的库存问题的研究起源于血库中血液的库存管理.对血液来说，如果库存血液过多，则必有一部分以前采集的血液由于未得到及时使用而过期报废；如果库存血液不足，则在出现突发事故时可能会因此而耽误对病人的抢救甚至造成病人的死亡.Ghare等[1]首次考虑了单级库存中确定需求情况下易变质商品的库存模型；Balkhi[2]在需求率、生产率随时间变化的条件下，提出了一对一的易变质商品的生产策略；Covert等[3]深入研究了易变质物品的大批量配送问题；Nahmias[4-5]研究了易变质物品库存系统的订货策略；Dave等[6]在需求与时间成比例、瞬时补货、不允许缺货的假设条件下开发了易耗品的库存模型；Lin[7]建立了供应商和用户之间的一对一合作模型，解决了不可维修的有一定损坏概率情况下的二阶段梯形模型的合作问题，但是当考虑该模型中的n个周期中需求速度、储费、缺货费、订购费等是常数的情况下，则可以按照类似于EOQ模型中平均时间上库存费用的解决办法来求解，没必要考虑n个周期，并且销售商库存水平呈指数增长.本文通过将供应商和销售商之间的二级库存的合作问题转化为一个生产商自给自足的生产问题，建立了供应商和销售商的易变质商品的库存控制数学模型，解决了文献[7]中存在的问题.

1 本库存模型涉及的基本假设

（1）考虑二级库存的模式，即是一个供应商和一个销售商.

（2）设考察n个周期，总的时间为t＞0.

（3）在第i个周期中（0＜i＜n），单位存储费用为ci1，单位缺货费用为ci2，订购费用为ci3，需求速度为Di.

（4）假定商品在运货途中以及在存储状态，它的寿命函数均服从指数分布，且分布为F（t）=1-e-λt，t＞0.其中，λ为参数，表示单位时间内商品变坏的个数，即变质率.

（5）假设在运输过程中备运期Ti也服从指数分布，且分布为F（Ti）=1-eLiTi，Ti＞0.其中，Li为参数，它表示单位时间到货的个数；

（6）设Qi（t）表示销售商的库存水平；tpi表示第i周期的最大库存量的时刻；Q1i表示第i周期的最大库存量；Qi表示第i周期应该订购的数量，即第i周期订购批量；Si（t）表示备运期的库存水平；

（7）设si表示在第i周期中商品用完的时刻；ti表示在第i周期中开始订货的时刻.

（8）设CCi表示在第i周期中的总存储费用；CQi表示在第i周期中的总缺货费用；Ci表示在第i周期中的总费用；C表示n个周期的总费用.

2 库存控制模型

2.1 优化模型

正因为易变质商品的寿命服从指数分布，根据指数分布的无记忆性，可以把一个供应商和一个销售商的二级库存模式看作是一个生产商自给自足的生产模式，也可以看作是供应商和销售商合作的结果.

模型的优化过程如下：

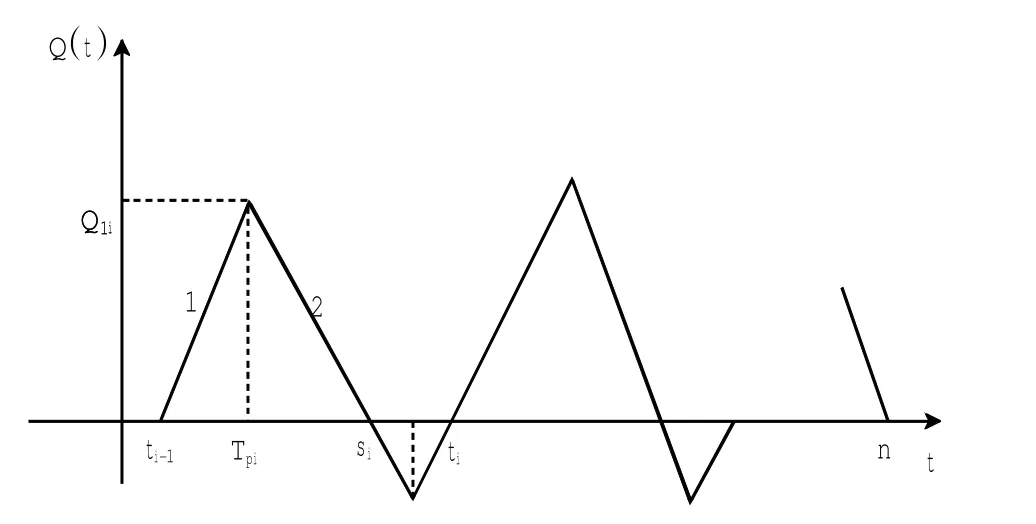
图1 二级库存控制模型Fig.1 Two levels of inventory control model

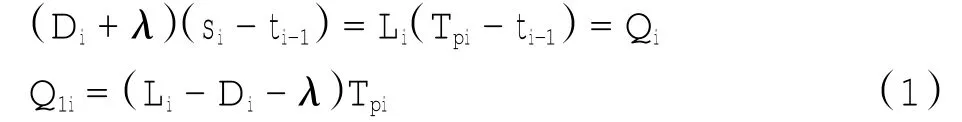
（3）第i周期中的总存储费用CCi，即为Δti-1Q1isi的面积乘以ci1，算得：

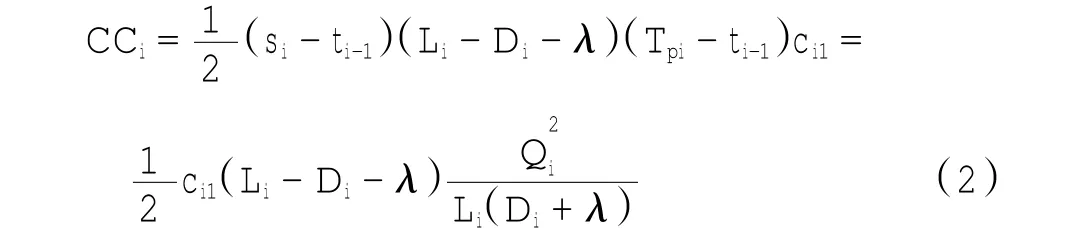
（2）订购的数量与销售的数量相等，所以有

（4）第i周期中的总缺货费用CQi，即为[si，ti]区间上的那个小三角形的面积乘以ci2，可得：

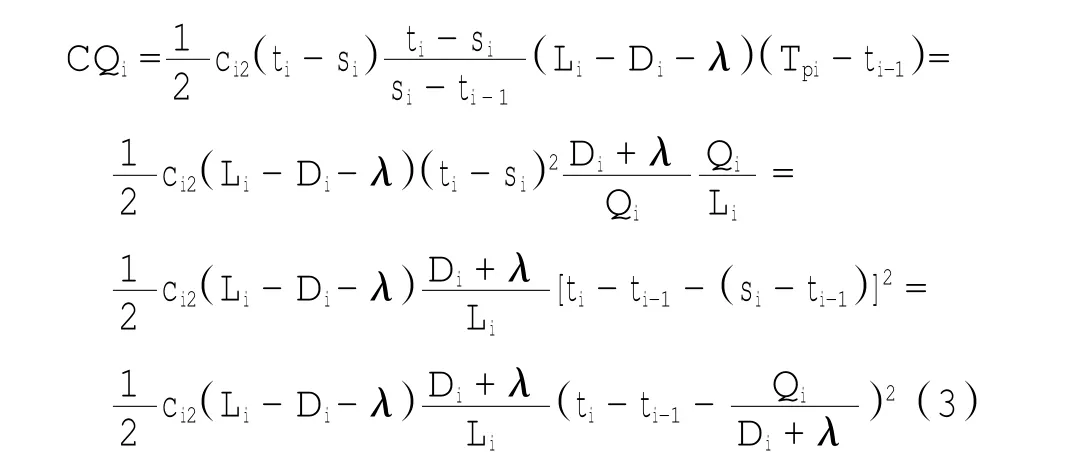
（5）第i周期中的总费用为：

这里需要注意的是在第n个周期中就没有了缺货费

用，所以第n周期的总费用为：

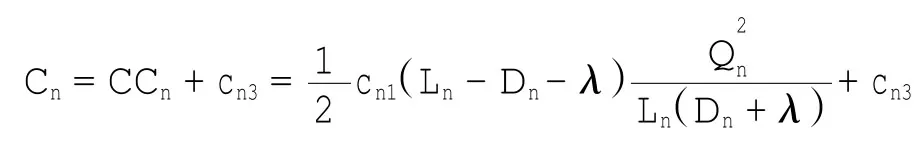
则[0，t]时间内的总费用为：

2.2 模型的求解

2.3 模型的对比

本文通过将供应商和销售商之间的二级库存合作问题转化为一个生产商自给自足的生产问题，建立了供应商和销售商的易变质商品的库存控制数学模型.本文与文献[7]的详细差别如表1所示.

3 算例仿真

表1 本文与文献[7]的关系Tab.1 Relationship between this article and document[7]

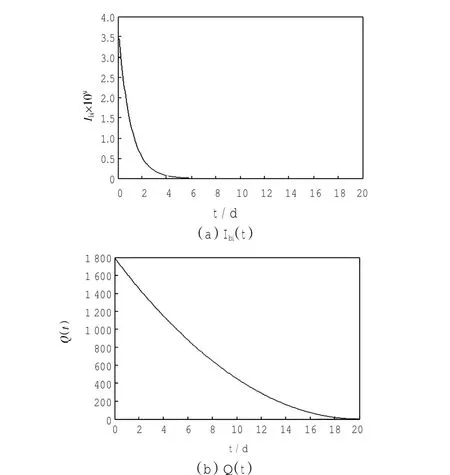
图2 销售商库存水平变化Fig.2 Change of sellers inventory levels

由图2中的曲线可以看出，本文销售商的库存水平变化曲线比较平缓，避免了库存成本的提高.

4 结束语

本文考虑了在时间为t的限制下易变质商品的一对一的库存模型，提出了合作库存的一种新的转换方法，采用每个阶段上的平均费用的方法，解决了销售商库存水平呈指数增长的问题.但是这种模型只是对于特殊的指数分布满足，因此该研究还需要深入到满足一般分布的模型，得到更实用的结论.

[1]GHARE P M，SCHRADER S F.A model for exponentially decaying inventory[J].Journal of Industrial Engineering，1963, 14：238-243.

[2]BALKHI Z T，BENKHEROUF L.A production lot size inventory model for deteriorating items and arbitrary production and demand rates[J].European Journal of Operational Research, 1996，92：302-309.

[3]COVERT R P，PHILIP G C.An EOQ model for items with weibull distribution deterioration[J].IIE Transactions,1973，5：323-326.

[4]NAHMIAS S.Optimal ordering policies for perishable inventory-II[J].Operations Research，1975，23：735-749.

[5]NAHMIAS S.Perishable inventory theory:A review[J].Operations Research,1982，30：680-708.

[6]DAVE U，PATEL L K.（T，Si）policy inventory model for deteriorating items with time proportional demand[J].Jounral of Operational Research Society，1981，32：137-142.

[7]LIN C H，LIN Y S.A cooperative inventory policy with deteriorating items for a two-echelon model[J].European Journal of Operational Research，2007，178：92-111.

[8]司书宾，贾大鹏，兑红炎，等.带有横向调度的两级维修备件库存系统优化方法研究[J].西北工业大学学报，2008，26（6）：765-770.

Cooperative strategies of two levels inventory model with perishable goods

LI Bin1，PAN Xiu-juan2，FAN Chang-sheng1
（1.Project Management Department，Shaanxi Radio and TV University，Xi′an 710068，China；2.School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

Considered the inventory control policy issues of two levels inventory system with perishable goods，the inventory control mathematical model for perishable goods is established between suppliers and sellers under the demand rate and the deterioration rate determined.It assumes that the life distribution function for perishable goods is exponentially distributed.Meanwhile，the problem of two levels cooperation between suppliers and vendors is transformed into the issue of a self-sufficient production manufacturer.Finally，the accuracy of the model and solution algorithm is conformed by the simulation of a numerical example.Compared with traditional methods，the optimal inventory control parameters are found.The inventory of vendor stocks will be avoided with increasing exponentially.

life distribution function；perishable；inventory levels；control parameters

O227

A

1671-024X（2013）04-0076-03

2012-12-11

陕西省自然科学基金资助项目（2011JQ1017）；陕西省教育厅自然科学专项基金资助项目（2012JK0872）

李斌（1978—），男，硕士，讲师，E-mail：libinsxdd@126.com