一类具有免疫损害项的带时滞的病毒感染模型分析
2013-07-07张晓黄东卫郭永峰
张晓,黄东卫,郭永峰
(天津工业大学理学院,天津 300387)
一类具有免疫损害项的带时滞的病毒感染模型分析
张晓,黄东卫,郭永峰
(天津工业大学理学院,天津 300387)
对一类具有免疫损害项的带时滞的病毒感染模型进行了动力学分析,研究未感染平衡点的全局稳定性,并给出感染平衡点产生Hopf分岔的充分条件;数值模拟验证了主要分析结果,从而解释了免疫反应的复杂性.
免疫损害;时滞;稳定性;Hopf分岔;病毒感染模型
自1981年在美国发现艾滋病(AIDS)以来,人类免疫缺陷病毒(HIV)感染迅速在世界范围内传播,从而引起了医生、生物学家、数学家的注意.尽管他们在艾滋病研究方面取得了很多成果,但仍有很多的艾滋病发病机理是未知的.最近,在治疗艾滋病方面,大量的数学模型被应用于分析体内艾滋病病毒的数量动态,从而使研究人员可以更好的了解艾滋病病毒的感染过程以及不同药物治疗所产生的效果.研究发现HIV主要的攻击对象是体内的CD4+T细胞,而主要的驱赶者是免疫反应[1],其中细胞毒T淋巴细胞(CTLs)通过作用于病毒感染细胞而在抗病毒防御机制中起重要作用.慢性HIV感染引起CD4+T细胞总量的减少,从而降低了人体抵御感染的能力,最终导致艾滋病的产生.本文将建立数学模型对HIV感染进行研究.
1 提出模型
近几十年来,许多学者建立了不同的HIV感染模型来研究艾滋病的发病机理.文献[2]建立了一个描述易感寄主细胞、感染细胞、病毒及CTLs之间数量关系的数学模型.然而自由病毒颗粒的周转率显著快于感染细胞的周转率[3-4],因此可以做一个半稳定性假设,那么自由病毒颗粒的数量就简单正比于感染细胞的数量.由此得到王开发等[5]构造的描述易感寄主细胞、感染细胞及CTLs之间的数量关系的数学模型:
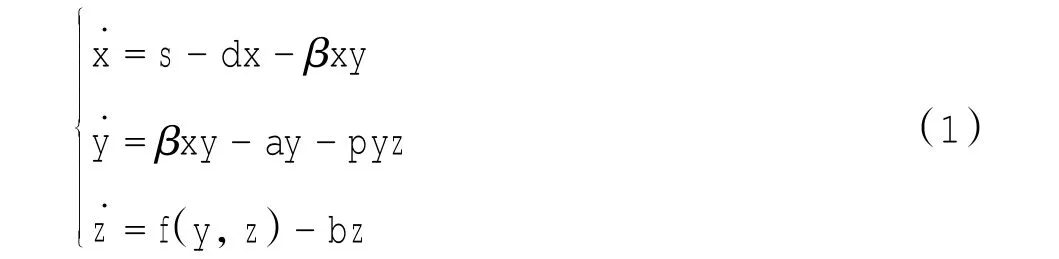
式中:f(y,z)表示CTLs遭遇感染细胞后的生长速率.由于机体免疫反应的复杂性,函数f在不同的假设机制下有不同的表达形式[6-7].在病毒感染过程中,被引诱的寄主细胞最初并没有专门杀死病毒的细胞,然而在一段时间之后,会产生专门杀死病毒的细胞,即细胞毒T淋巴细胞(CTLs)或抗体细胞.也就是说,从抗原刺激到产生CTLs需要一段时间τ,即在时刻t的CTLs反应实际上取决于t-τ时的抗原的刺激.故对于免疫反应,时滞是不能忽略的[5,8-10].然而,模型(1)只考虑了抗原能够激发免疫力,而忽略了免疫损害.实际上有大量的实验表明病毒产生变异后,可以逃避免疫反应[11-13].也就是说,抗原不只是能激发免疫力,也能够抑制免疫反应,甚至损害免疫力.故本文把免疫损害项myz引入到模型中,从而得到以下模型:

式中:x、y、z分别表示易感寄主细胞、感染细胞和CTLs的数量;易感寄主细胞以常数s速率产生,以dx速率死亡,并以βxy速率变为感染细胞;感染细胞以速率ay死去,并以pyz速率被免疫细胞杀死;CTLs的产生依赖于τ时刻之前的感染细胞的数量,故ce-aτy(t-τ)为CTLs的增值率,且它以bz速率衰亡,myz速率受到免疫损害.进而,p表示免疫反应率,m表示免疫损害率,τ表示时滞.
系统(2)的初值为.

2 基本结论
首先讨论系统(2)的平衡点.
记基本再生数R0=sβ/(ad),很容易证明出:
(1)当R0<1时,系统(2)仅有一个未感染平衡点E0=(x0,0,0),这里x0=s/d;
(2)当R0>1时,除了未感染平衡点E0外,系统(2)还有另外一个感染平衡点E1=(x1,y1,z1),这里

首先给出一个定理,说明系统(2)为耗散系统,即其解始终为正并且最终有界.
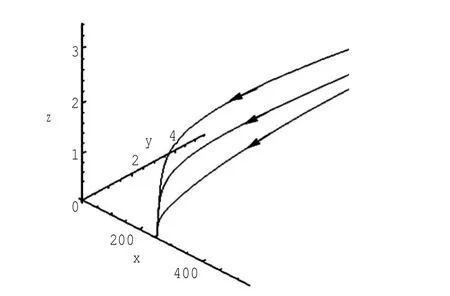
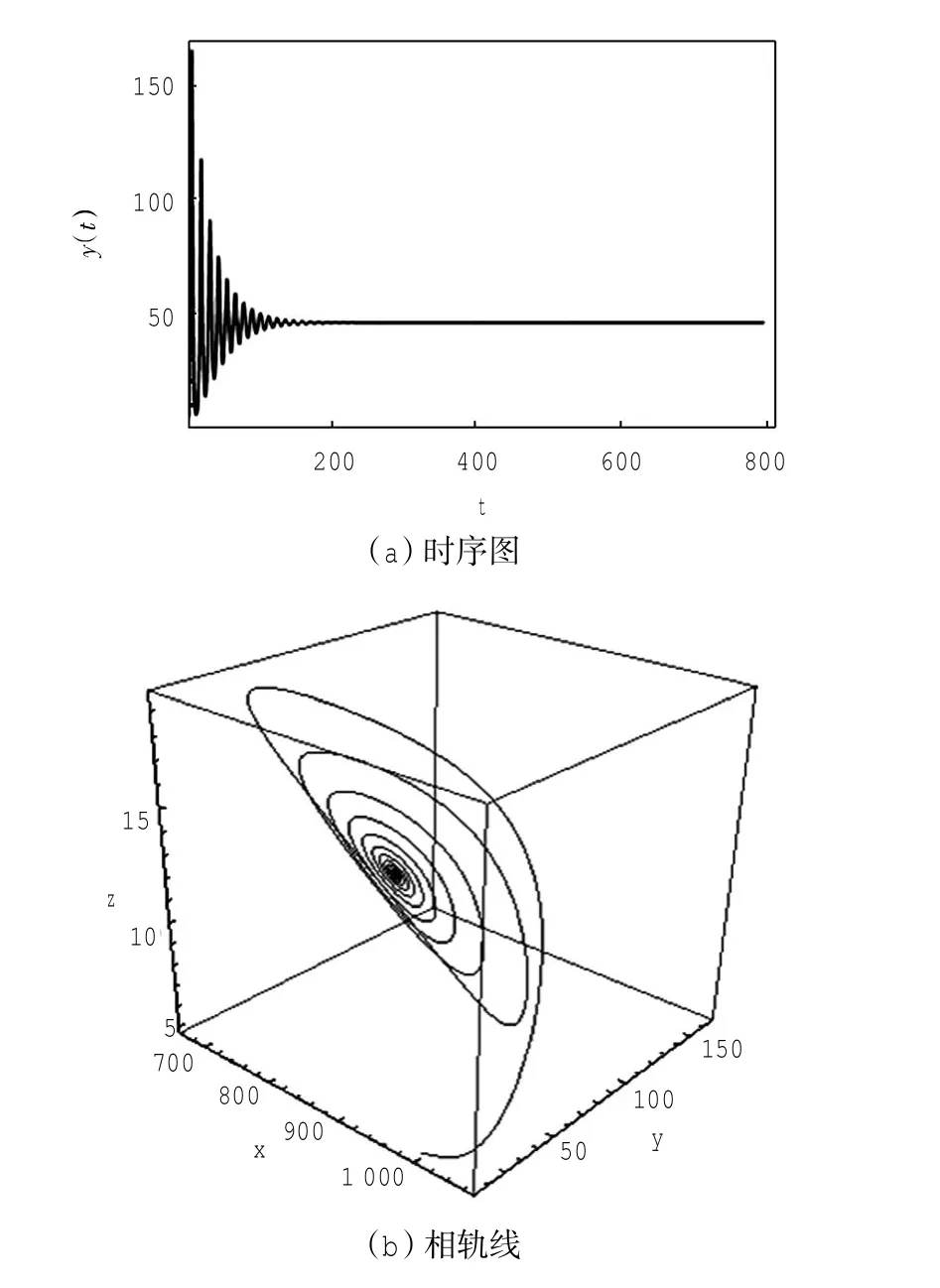
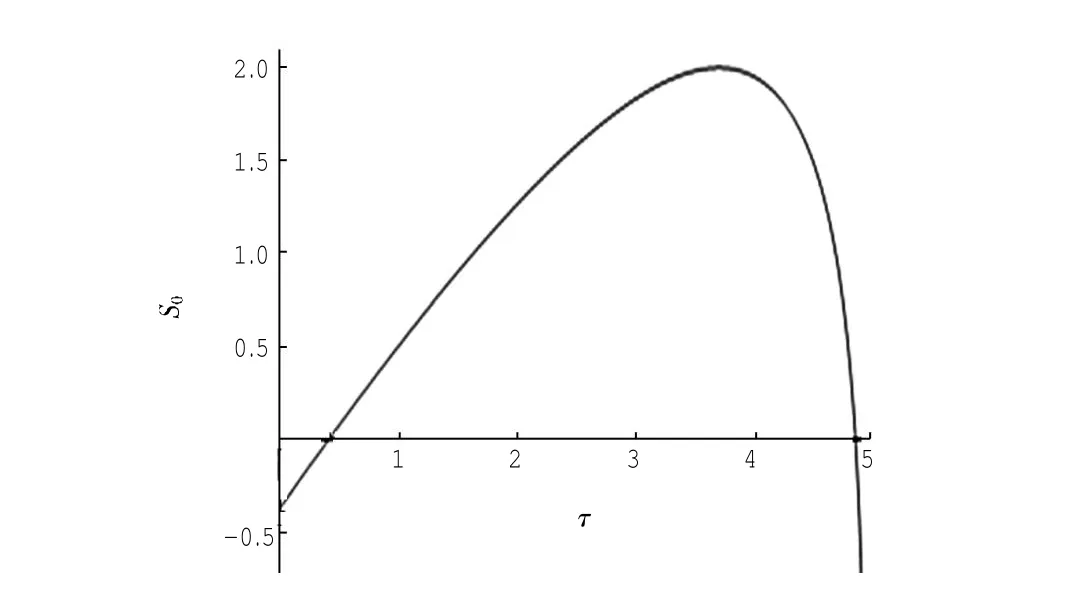
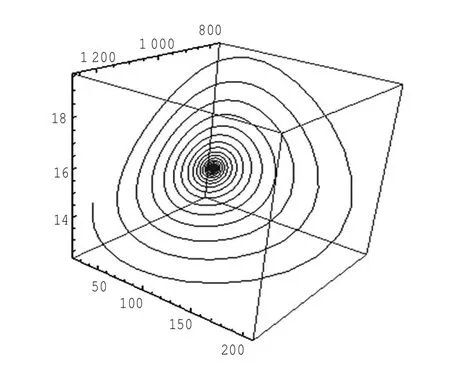
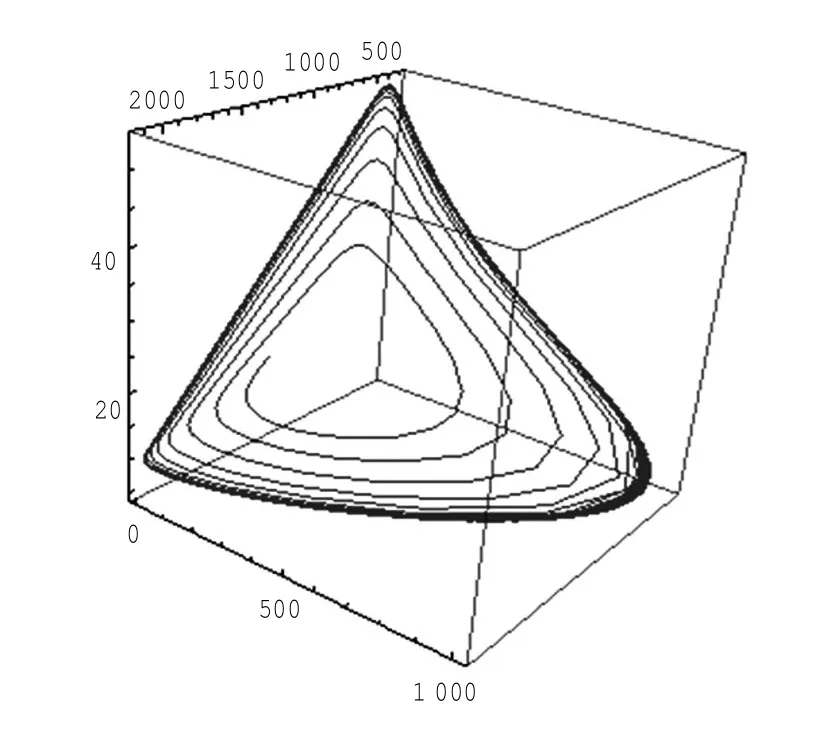
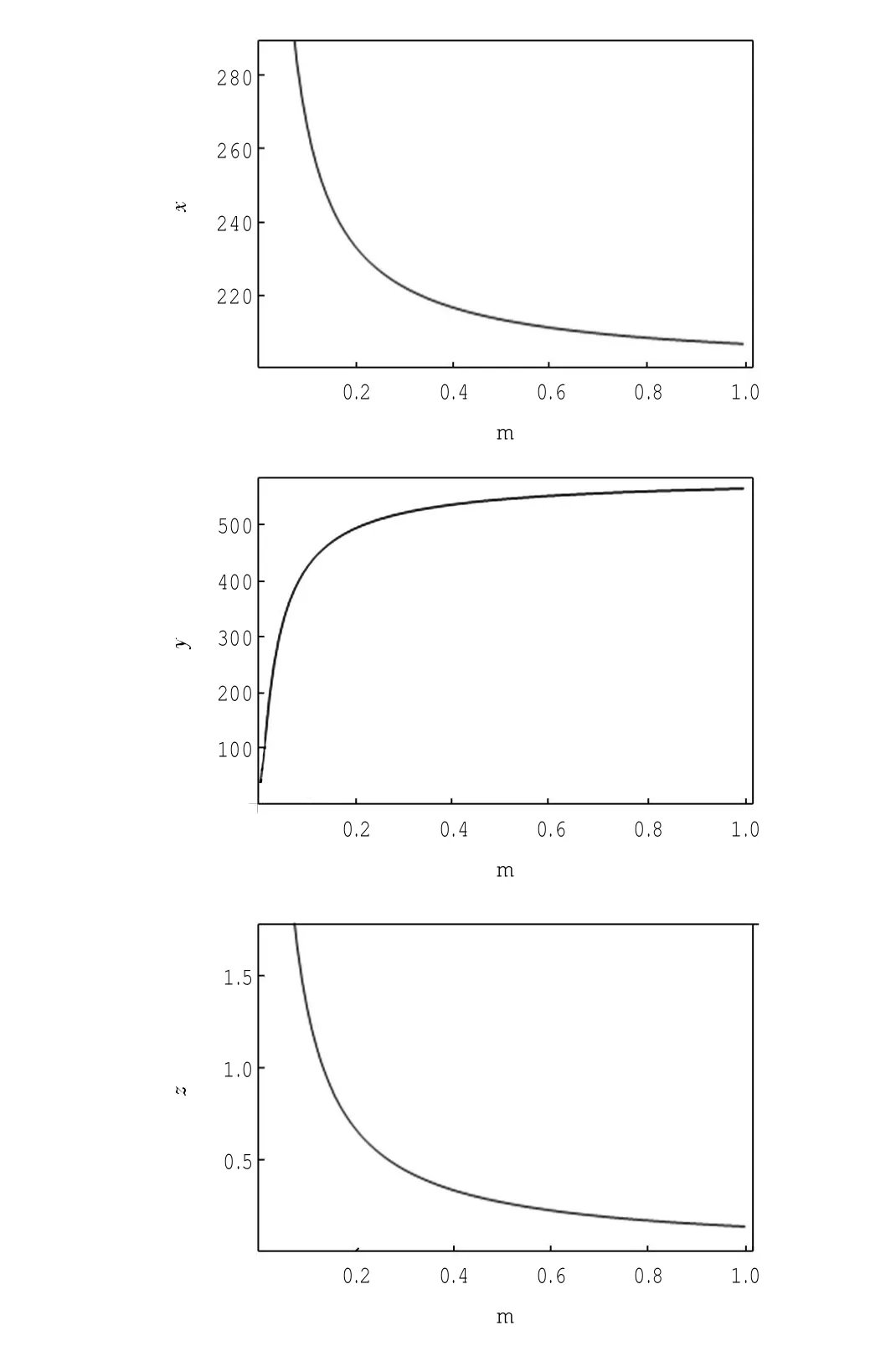
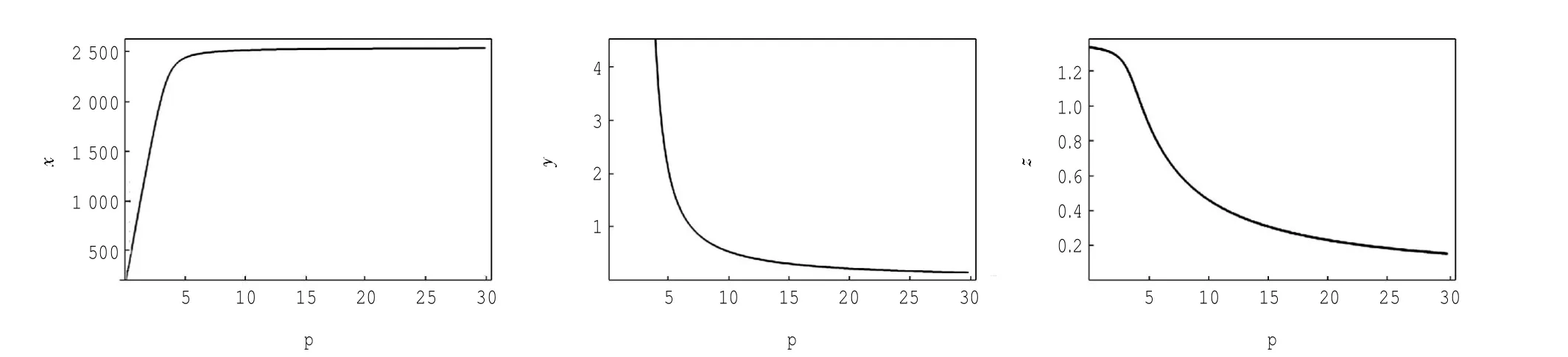
定理1对于t≥0,在初值条件(3)下,系统(2)的所有解(x(t),y(t),z(t))都是正的,并且存在一个常数M>0,对充分大的t有x(t) 证明:假设x(t)不恒为正,则存在最小的t0>0,使得x(t0)=0,根据系统(2)的第1个等式,则有=s> 0,也就是说,存在一个足够小的ε>0,对于t∈(t0-ε,t0)有x(t)<0,又x(0)=ψ1(0)>0,则至少存在一个∈(0,t0-ε)使得x(t0*)=0.这与t0>0为第一个使x(t)为0的时刻矛盾.所以x(t)始终为正.进而,由系统(2)的(2)、(3)式可知 由于参数c>0,显然有y(t)、z(t)在存在区间内为正. 接着,证明系统(2)的所有解最终是有界的.设F(t)=x(t)+y(t)+aeaτz(t+τ)/(2c),由于系统(2)的所有解及参数都为正,故有F′(t)≤s-dx-ay/2-pyzabeaτz(t+τ)/(2c)≤s-μF(t),其中μ=min{d,a/2,b}.易知F(t)≤s/μ+(F(0)-s/μ)e-μt.所以存在一个常数M>0,使得x(t) 本文对系统(2)的2个平衡点进行了研究,并给出一些定理,从而为今后的药物开发及艾滋病的治疗提供一定理论基础. 定理2当R0<1时,未感染平衡点E0是全局渐近稳定的;当R0>1时,未感染平衡点E0是不稳定的. 证明:系统(2)在E0处的特征方程为(λ+d)(λ+ b)(λ+a-βx0)=0.很明显看到λ1=-d<0,λ2=-b< 0,若R0<1,则λ3=βx0-a<0,这就证明了特征方程无正根,则未感染平衡点E0是局部渐近稳定的;然而当R0>1时,有λ3=βx0-a>0为特征方程的一个根,故未感染平衡点E0是不稳定的. 下面讨论未感染平衡点E0的全局渐近稳定性,构造Lyapunov函数如下: 由于R0<1与a-βx0>0等价,故这里ε=ax0->0.计算V(t)沿着系统(2)的导数, 注意到x(t)、y(t)、z(t)是正的,那么当R0<1时,有V′(t)≤0,并且V′(t)=0当且仅当(x,y,z)=(x0,0,0).由Lyapunov-LaSalle定理可知,当R0<1时,E0是全局渐近稳定的.当R0<1时,时滞τ不影响未感染平衡点E0的稳定性. 接下来,把τ作为参数来研究感染平衡点E1的稳定性以及Hopf分岔的存在性.系统(2)在E1处的线性系统对应的特征方程为:其中 首先考虑τ=0时,感染平衡点E1的局部稳定性.此时,(4)式可化简为λ3+B1λ2+B2λ+B3=0, 其中 由Routh-Hurwitz准则,可得如下定理: 定理3如果R0>1且τ=0,感染平衡点E1是局部渐近稳定的. 首先讨论(4)式纯虚根λ=iω(ω>0)的存在性.方程(4)是λ的三次指数多项式,P和Q的所有参数都是τ的函数.Beretta[14]和Li[15]给出了参数依赖于时滞的特征方程纯虚根存在的定理,为了应用此定理,需要先对τ∈[0,τmax)验证以下性质,这里τmax为E1存在的最大τ值. (a)P(0,τ)+Q(0,τ)≠0,∀τ∈R+0; (b)如果λ=iω(ω∈R),则P(iω,τ)+Q(iω,τ)≠0,∀τ∈R+0; (c)对于任意τ,lim sup{|Q(λ,τ)/P(λ,τ)|∶|λ|→∞,Reλ≥0}<1; (d)对于每个τ,F(ω,τ)=|P(iω,τ)|2-|Q(iω,τ)|2最多有有限个零根; (e)F(ω,τ)的每个正根ω(τ)对τ是连续可微的. 易知P(0,τ)+Q(0,τ)=β2x1y1(b+my1)+bpz1(d+ βy1)]≠0,ω(τ)是(9)的正根. 引进I→R上的一个函数Sn(τ):=τ-τn,n∈N0,τ∈I,根据文献[14,15]可知: 为了验证以上的理论分析,本文进行了数值模拟,并且参考了文献[5,8,9]中的参数选取,通过数学软件Mathematica7.0得到以下结果.首先,选取s=255、d= 1、β=0.002、a=1、p=0.1、c=0.2、b=0.1、m=0.1,此时R0=0.51<1,满足定理2,则系统(2)仅有一个未感染平衡点E0=(255,0,0),且时滞τ不影响其稳定性,图1验证了这个事实. 图1 τ=0.1、1、5时,系统(2)的相轨线Fig.1Phase trajectories of system(2)with τ=0.1,1,5 另外,选取s=255、d=0.2、β=0.002、a=0.4、p=0.1、c=0.2、b=0.1、m=0.01、τ=0.5,此时R0= 6.375>1,则系统(2)除了未感染平衡点E0外,还有感染平衡点E1,并且E0是不稳定的.由图2可知,系统(2)的相轨线收敛到E1=(872.8,46.1,13.5). 进而,用数值来模拟时滞τ的改变将会引起系统稳定性的改变以及Hopf分岔的发生.考虑参数s= 255、d=0.1、β=0.002、a=0.4、p=0.1、c=0.2、b=0.1、m=0.01,绘制了在I中S0关于τ的图像,如图3所示. 图2 y(t)的时序图以及系统(2)的相轨线Fig.2 Timing chart of y(t)and phase trajectory of system(2) 图3 在I上S0关于τ的图像Fig.3 Graph of S0versus τ on I 由图3可以看到对于时滞τ,有一个临界值τ*且τ*≈0.4.由定理5可知,当τ∈(0,τ*)时,感染平衡点E1是局部渐近稳定的,当τ在τ*的某个右邻域时,E1变得不稳定,τ=τ*时系统(2)产生一个Hopf分岔.图4和图5验证了分析结果,图4显示τ=0.35时系统的相轨线收敛到E1=(973.8,80.9,15.5),图5显示当τ=0.5时,系统产生一个周期解. 由于R0=sβ/(ad),可知R0的大小与免疫反应率p及免疫损害率m都没有关系.图6与图7分别给出了当s=255、d=0.1、β=0.002、α=0.4、p=0.1、c=0.2、b=0.1、τ=1时,感染平衡点的坐标(x,y,z)关于免疫损害率m及免疫反应率p的变化趋势图. 图4 τ=0.35时系统的相轨线Fig.4 Phase trajectory of system with τ=0.35 图5 τ=0.5时系统的相轨线Fig.5 Phase trajectory of system with τ=0.5 由图6可以得知,随着免疫损害率m的增大,感染细胞的数量也在增加,而未感染细胞量及CTLs细胞量在减少.而由图7可以得知,随着免疫反应率p的增大,未感染细胞量在增加,而感染细胞量及CTLs细胞量在减少.而此时R0=12.75>1,由定理(2)可知,系统(2)在未感染平衡点是不稳定的,故感染细胞不可能被全部杀死,而只可能是感染细胞量在逐渐的减少,由图7还可以得知,它逐渐地接近于0,而不能达到0.这也就说明了仅靠宿主免疫系统的活性通常不足以完全消灭体内病毒,最多仅能降低体内病毒感染的强度. 图6 感染平衡点的坐标x,y,z关于免疫损害率m的变化趋势图.Fig.6 Graph x,y and z(axies of infected equilibrium)as functions of immune impairment rate m 图7 感染平衡点的坐标x,y,z关于免疫反应率p的变化趋势图Fig.7Graph x,y and z(axies of infected equilibrium)as functions of immune response rate p 本文从理论上和数值上分析了一类具有免疫损害项的带时滞的病毒感染模型.证明出:当基本再生数R0<1时,未感染平衡点是全局渐近稳定的,即对于任意时滞τ≥0,宿主体内的病毒都会被清除从而疾病将会痊愈;当基本再生数R0>1时,宿主体内的病毒将会永久存在,并且存在一个时滞τ*>0,当τ<τ*时,宿主体内的病毒将会稳定到一个正平衡点,然而当τ稍大于τ*时,宿主体内的病毒将会呈现出周期震荡.这些结果能够解释免疫反应的复杂性,同时也符合研究人员临床观测的结果. [1]WANG Y,ZHOU Y,WU J,et al.Oscillatory viral dynamics in a delayed HIV pathogenesis model[J].Math Biosci,2009,219:104-12. [2]WODARZ D,KRAKAUER D C.Defining CTL-induced pathology:Implications for HIV[J].Virology,2000,274:94-104. [3]BARTHOLDY C,CHRISTENSEN J P,WODARZ D,et al. Persistent virus infection despite chronic cytotoxic T-lymphocyte activa-tion in Gamma interferon-deficient mice infected with lymphocytic choriomeningitis virus[J].J Virol,2000,74:10304-10311. [4]WODARZ D,CHRISTENSEN J P,THOMSEN A R.The importance of lytic and non-lytic immune response in virus infections[J].Trends Immunol,2002,23:194-200. [5]WANG K,WANG W,PANG H,et al.Complex dynamic behavior in a viral model with delayed immune response[J]. Physica D,2007,226:197-208. [6]DE BOER R J,PERELSON A S.Towards a general function describing T cell proliferation[J].J Theoret Biol,1995,175:567-576. [7]DE BOER R J,PERELSON A S.Target cell limited and immune control models of HIV infection:A comparison[J].Theoret Biol,1998,190:201-214. [8]CANABARRO A A,GLÉERIA I M,LYRA M L.Periodic solutions and chaos in a non-linear model for the delayed cellular immune response[J].Physica A,2004,34(2):234-241. [9]王永昭,黄东卫,张双德,等.一类具有免疫时滞的HIV感染模型分析[J].天津工业大学学报,2011,30(3):76-80. [10]SONG X,WANG S,ZHOU X.Stability and Hopf bifurcation for a viral infection model with delayed non-lytic immune response[J].J Appl Math Comput,2010,32:251-265. [11]PHILLIPS E R,ROWLAND-JONES S,NIXON D F,et al. Human immunodeficiency virus genetic variation that can escape cytotoxic T cell recognition[J].Nature,2005,354:453-459. [12]BRROWP,LEWICKI H,WEI X,et al.Antiviral pressure exerted by HIV-1 pecific cytotoxic T lymphocytes(CTLs)during primary infection demonstrated by rapid selection of CTL escape virus[J].Nat Med,1997,3(2):205-211. [13]GOULDER P J R,PHILLIPS R E,COLBERT R A,et al. Late escape from an immunodominant cytotoxic T-lymphocyte response associated with progre ssion to AIDS[J].Nat Med,1997,3(2):212-217. [14]BERETTA E,KUANG Y.Geometric stability switch criteria in delay differential systems with delay dependent parameters [J].SIAM J Math Anal,2002,33:1144-1165. [15]LI J,MA Z.Stability switches in a class of characteristic equations with delay-dependent parameters[J].Nonlinear Analysis:Real World Applications,2004(5):389-408. [16]HALE J,LUNEL S V.Introduction to Functional Differential Equations[M].New York:Springer,1993. Analysis of a delayed viral infection model with an immune impairment term ZHANG Xiao,HUANG Dong-wei,GUO Yong-feng The dynamic behavior of a delayed viral infection model with an immune impairment term is analyzed.The globally stability of the viral free equilibrium is investigated,and the sufficient conditions of the existence of Hopf bifurcation around infected equilibrium are studied.Numerical simulations are carried out to illustrate the main results,which can explain the complexity of immune response. immune impairment;time delay;stability;Hopf bifurcation;viral infection model O193 A 1671-024X(2013)04-0079-06 2012-10-25 :国家自然科学基金资助项目(11102132) 张晓(1990—),女,硕士研究生. 黄东卫(1966—),男,博士,教授,硕士生导师.E-mail:tjhuangdw@163.com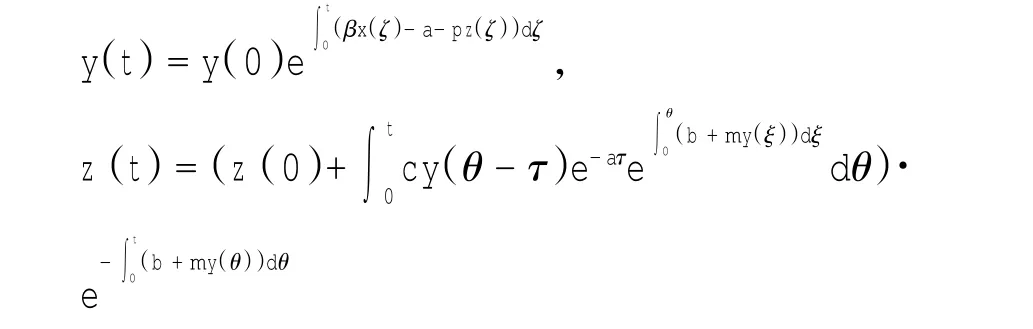
3 平衡点的稳定性分析
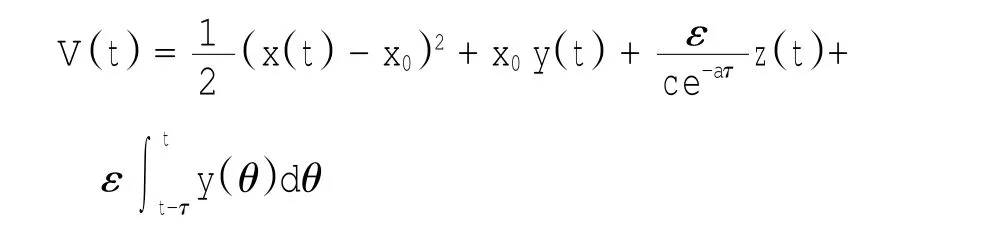
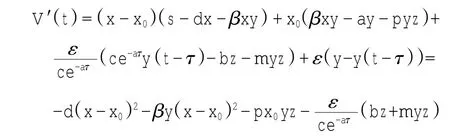

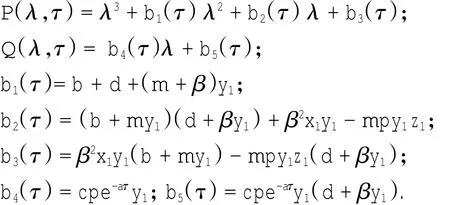
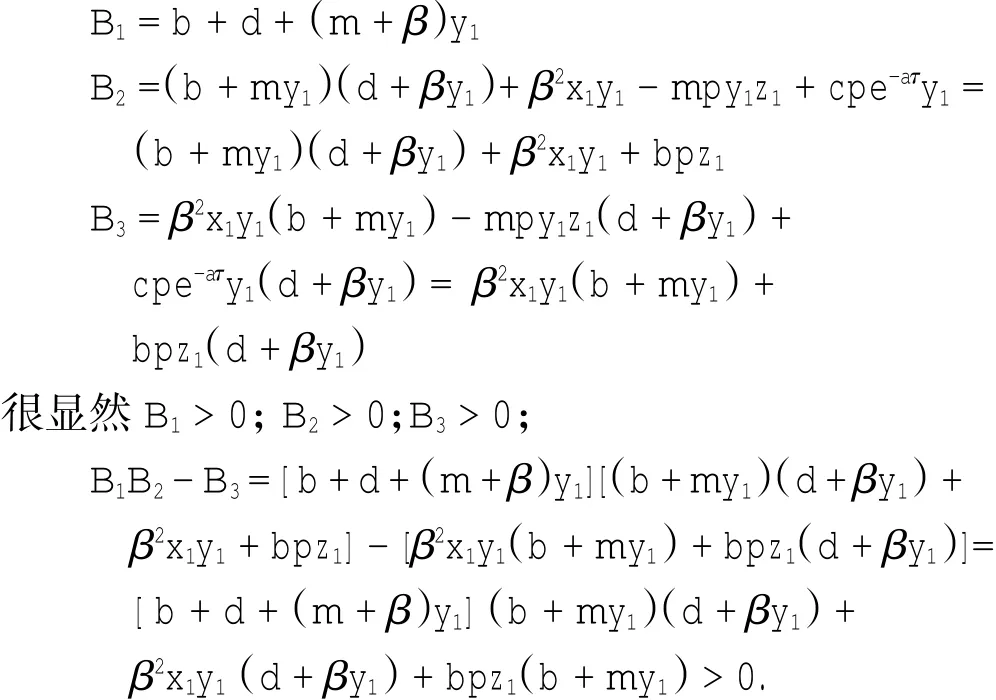


4 数值模拟
5 结论
(School of Science,Tianjin Polytechnic University,Tianjin 300387,China)
