带有时变时滞的非线性系统的指数稳定

杨凤伟，董亚丽

（天津工业大学理学院，天津 300387）

带有时变时滞的非线性系统的指数稳定

杨凤伟，董亚丽

（天津工业大学理学院，天津 300387）

研究一类带有时变时滞的非线性系统的指数稳定性问题.通过构造适当的Lyapunov-Krasovskii泛函，并结合使用Newton-Leibniz公式和自由权方法，对这类系统建立了以线性矩阵不等式表达的依时滞的指数稳定的新的充分条件；对于带有常时滞的一类非线性系统，给出了系统指数稳定的判据，并以数值例说明所获结果的有效性.

非线性系统；指数稳定；时变时滞；Lyapunov-Krasovskii泛函；线性矩阵不等式（LMI）

时滞经常出现在人口模型、化学过程、生物及经济系统等众多实际系统中.众所周知时滞的存在常引起系统的不稳定和差的性能，因此对时滞系统稳定性的研究引起了研究者的关注，并成为重要的研究主题[1-7].近年来，人们对于带有时变时滞的线性系统的指数稳定性已经作了深入的研究，并获得了一些指数稳定性判据[1-4].然而，对于带有时变时滞的非线性系统的指数稳定性研究却很少.本文研究一类带有时变时滞的非线性系统的指数稳定性问题.首先通过构造适当的Lyapunov-Krasovskii泛函，结合使用Newton-Leibniz公式和自由权方法，获得了该类系统指数稳定的充分条件.然后针对带有常数时滞的非线性系统进行了研究，并给出了这类系统指数稳定的充分条件.

1 问题描述及预备知识

本文的符号说明如下：R+表示所有非负实数的全体；Rn表示n维向量空间，且有向量内积xTy及向量范数||·||；Rn×r表示所有以n×r维矩阵构成的空间；AT表示矩阵A的转置；I表示单位矩阵；λmax（·）和λmin（·）分别表示给定方阵的最大和最小特征值；A＞0表示A是正定的，A＞B表示A-B＞0.

考虑如下带有时变时滞的非线性系统

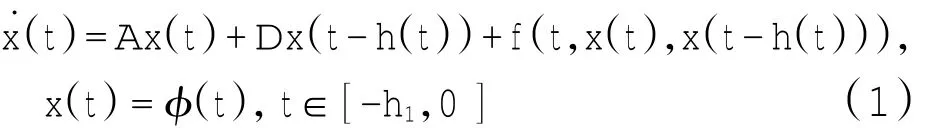
式中：x（t）∈Rn是状态；A，D∈Rn×n；初值φ（t）是定义在［-h1，0］上的连续可微函数，且有范数||φ||=

定义1[8]给定α＞0.系统（1）的零解称为是α指数稳定的，如果存在正数N＞0使得对任意解x（t，φ）有

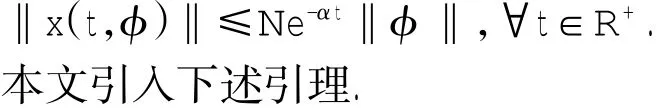
引理1[9]对于任意正定对称矩阵M∈Rn×n，标量γ＞0和向量函数ω∶[0，γ]→Rn使得所论积分有定义，则下述不等式

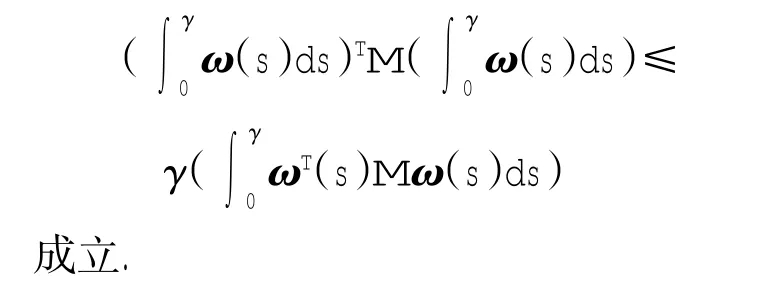
2 主要结果

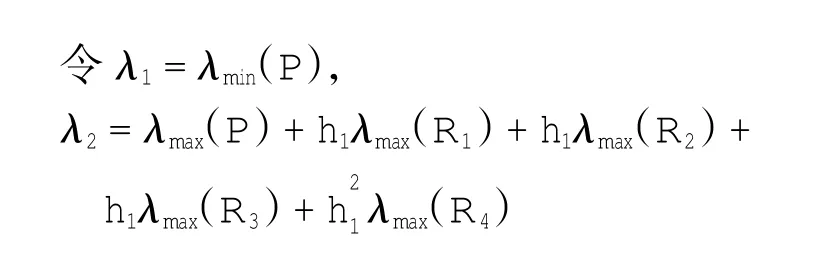
定理1给定α＞0.系统（1）的零解是α指数稳定的，如果存在正定对称阵P、R（ii=1，2，3，4）以及矩阵W（ii=1，2，3，4，5）和正数η＞0，使得下述LMI成立：

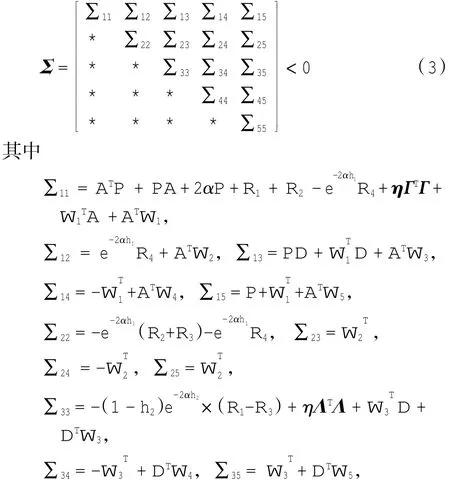
定理2给定α＞0.系统（12）的零解是α指数稳定的，如果存在正定对称阵P（i=1，2）以及矩阵，（i=1，2）和正数η＞0，使得下述LMI成立:

通过类似于定理1的证明可得系统（12）的零解是α指数稳定的.

3 数值例

考虑如下带有常数时滞的非线性系统[10]

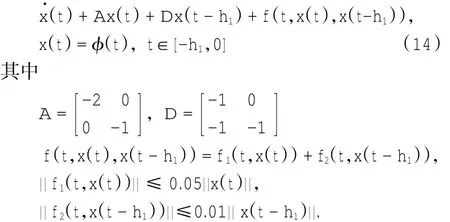
极易验证非线性函数f（t，x（t），x（t-h1））满足（2）式且

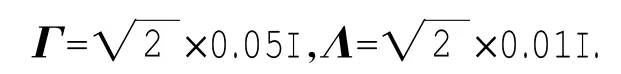
对α取不同的值，应用定理2，表1给出关于α时滞h1允许的上界.将本文结果与文献[10-12]的结果进行了比较.

表1 时滞允许的上界Tab.1 Allowable upper bound of delay h1

由表1可以看出，本文结果比文献[10-12]的结果具有更弱的保守性.

4 结束语

本文研究一类带有时变时滞的非线性系统的指数稳定性问题.通过构造适当的Lyapunov-Krasovskii泛函，并结合使用Newton-Leibniz公式和自由权技术，获得了系统指数稳定的新的充分条件，该条件以线性矩阵不等式表达.然后，对于带有常时滞的一类非线性系统，建立了系统指数稳定的新的充分条件.并给出数值例，与相关文献结果作对比，验证了本文所获结果的有效性.

[1]DE OLIVEIRA M C，GEROMEL J C，HSU I.LMI characterization of structural and robust stability：The discrete-time case [J].Linear Algebra Appl，1999，296：27-38.

[2]PHAT V N，NAM P T.Exponential stability and stabilization of uncertain linear time-varying systems using parameter dependent Lyapunov function[J].Int J Control，2007，80：1333-1341.

[3]PHAT V N，NIAMSUP P.A novel exponential stability condition of hybrid neural networks with time-varying[J].Vietnam J Math，2010，38：341-351.

[4]SUN Y J.Global stabilizability of uncertain systems with timevarying delays via dynamic observer-based output feedback[J]. Linear Algebra Appl，2002，353：91-105.

[5]DONG Y，LIU J，MEI S，et al.Stabilization for switched nonlinear time-delay systems[J].Nonlinear Analysis:Hybrid Systems，2011，5：78-88.

[6]PHAT V N.Switched controller design for stabilization of nonlinear hybrid systems with time-varying delays in state and control[J].Journal of the Franklin Institute，2010，347：195-207.

[7]董亚丽，范姣姣，杨迎娟，一类不确定时滞非线性系统的H∞鲁棒镇定[J].系统工程与电子技术，2009，31（5）：1167-1171.

[8]KHALIL H K.Nonlinear Systems[M].London:Prentice-Hall，1996.

[9]GU K，KHARITONOV V L，CHEN J.Stability of Time-Delay Systems[M].Boston：Birkhauser，2003.

[10]KWON O M，PARK J H.On robust stability criterion for dynamic systems with time-varying delays and nonlinear perturbations[J].Appl Math Comput，2008，203：937-942.

[11]KWON O M，PARK J H.Exponential stability for time-delay systems with interval time-varying delays and nonlinear perturbations[J].J Theory Optim Appl，2008，139（2）：277-293.

[12]NAM P T.Exponential stability criterion for time-delay systems with nonlinear uncertainties[J].Appl Math Comput，2009，214：374-380.

Exponential stability of nonlinear systems with time-varying delays

YANG Feng-wei，DONG Ya-li
（School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

The problem of exponential stability of a class of nonlinear systems with time-varying delays is investigated.By constructing the appropriate Lyapunov-Krasovskii functional and combined with Newton-Leibniz formula and free weighting matrix method，a new delay-dependent exponential stability sufficient condition for the class of systems is established in terms of linear matrix inequality（LMI）.Then，the exponential stability criterion for a class of nonlinear systems with constant delay is presented.Finally，a numerical example is provided to illustrate the effectiveness of the results obtained.

nonlinear system；exponential stability；time-varying delay；Lyapunov-Krasovskii functional；linear matrix inequality（LMI）

O17

A

1671-024X（2013）04-0085-04

2012-10-19

天津市自然科学基金资助项目（11JCYBJC06800）

杨凤伟（1989—），男，硕士研究生

董亚丽（1963—），女，博士，教授，硕士生导师.E-mail：dongyl@vip.sina.com