基于M/G/C排队模型的地铁人行通道宽度设置

金瑞俊，陈京荣，尉陇亮，崔笑川

(兰州交通大学数理与软件工程学院，兰州 730070)

近年来，大城市中的交通拥堵问题日益突出。地铁系统因其具备运行时间可靠、运行效率高、节能环保等优势成为解决拥堵问题的重要交通方式之一。而在地铁枢纽站中，人行通道是乘客的必经之路，不仅能直接体现车站的服务水平，而且也能衡量紧急情况下车站通道的疏散能力，因而通道的宽度的取值会直接影响到通道的通行能力。通道越宽，在满足通行能力的情况下，通道的建设成本也就越高;通道越窄，就会出现拥堵和排队过长的问题。因此，合理设置地铁人行通道宽度显得尤为重要。2010年，蒋阳升等［1］利用 c个M/G/1排队模型对地铁单向人行通道宽度进行了设计，并建立仿真模型对排队优化理论模型进行了验证。2009年，曹守华等［2］分析了地铁双向通道内行人的走行特性，建立了基于蚂蚁算法的元胞自动机模型，对双向通道内行人的自组织特性进行了充分的验证。2010年，张晋伟等［3］利用M/G/K排队模型对高速公路收费站设置方法进行了研究。但对于地铁双向通道，相关的文献一方面只是研究了单向通道的情况，另一方面只是对单个排队队列利用M/G/1排队模型进行了分析，具有局限性，所以本研究针对双向地铁人行通道，依据通道双向行人的自组织特性，对通道宽度的设计进行了全面考虑［4-10］。

1 地铁人行通道客流特性

1.1 通道内乘客的走行模式及M/G/C排队系统描述

1)通道内乘客的走行模式。依据对乘客的安全区域半径的描述，通道内乘客的走行模式分为3种情况:①干扰模式，即乘客之间距离很近，易发生身体接触，图1为每位乘客的安全区域半径相交。②合理模式，即乘客各自占有一定的活动范围，相互之间没有多余的空间，如图2所示。③舒缓模式，即乘客相互之间相距较远，各自行走的自由度较大，如图3所示。

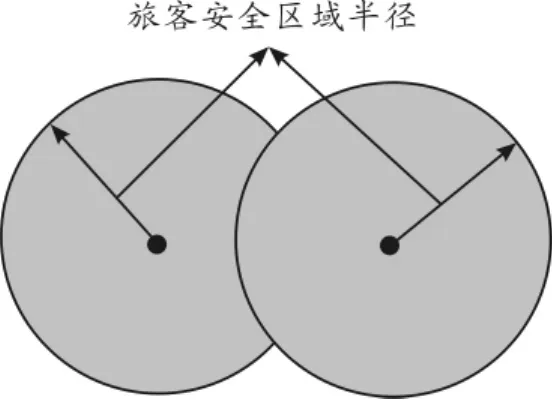
图1 乘客行走的干扰模式

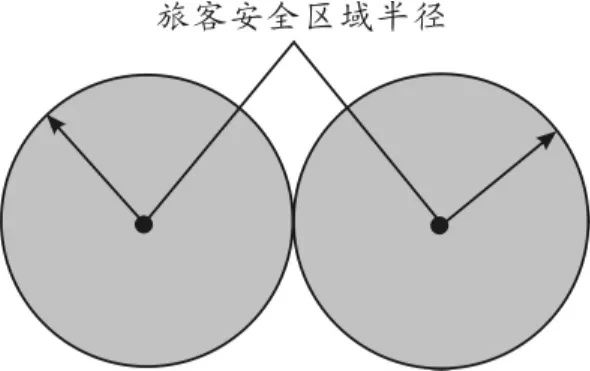
图2 乘客行走的合理模式

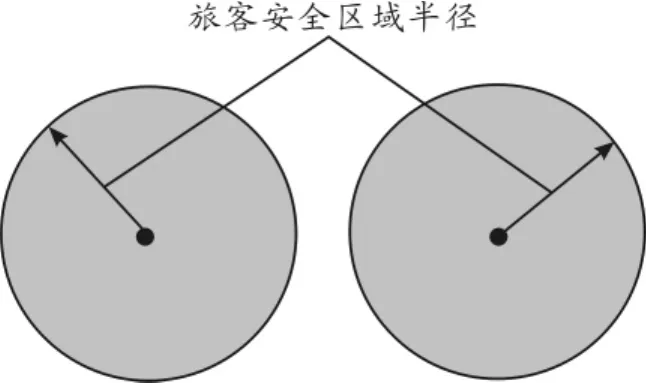
图3 乘客行走的舒缓模式

在乘客行走的干扰模式下，乘客之间的距离过于接近，以至于正常的行走会都受到影响。而对于舒缓模式下走行的行人，相互之间具有较大的间隙，在设计地铁通道的过程中，不能很恰当地反映出通道设计的实际最小宽度，因此，本研究采用乘客行走的合理模式进行分析。

2)M/G/C排队系统描述。M/G/C排队模型是指输入过程(乘客流到达)服从泊松分布(M)，且到达过程是平稳的，服务时间为随机分布(G)，有C个并联服务台，按照先到先服务的原则，不允许无限排队的一种网络排队模型。

在客流高峰时段，在通道的出口和入口处均出现排队情况。由于在客流量逐渐增大的过程中，双向通道内对向行人具有自组织特性，通道内行人由杂乱无章的分布逐渐显现出自组织特性。当客流量最大时，整个通道内行人系统趋于稳定，行人的自动化特性更加明显，因此，依据行人流将整个通道划分为相反方向的2个独立通道，分别利用M/G/C排队模型描述各自的排队系统。假设在通道的出口处沿通道宽度方向，并排设置了若干个无形的服务窗口，如图4所示。窗口的宽度即为前文所述的安全区域的直径，则通道的宽度为客流量最大时的最小窗口数。

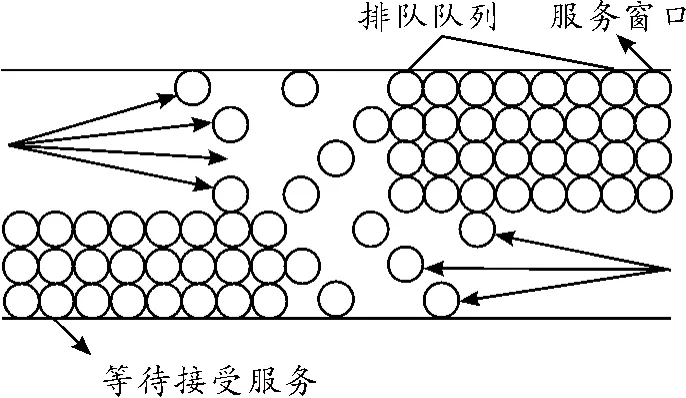
图4 双向通道排队系统

1.2 通道内双向行人的走行特性

通道内双向行人的走行特性为:①行人具有靠右行走的特性;②行人具有跟随行走的特性;③行人缺乏了解后方的交通信息;④行人有右侧避让对向行人的特性;⑤ 行人有趋向于选择最短路径到达目的地的特性;⑥在通道内无中央分割线时，若某个方向的行人流量较大，该方向行人会侵占对象的行人空间，使得整个通道的行人密度趋于均匀。

依据以上对行人走行特性的分析，通道内双向行人具有自组织特性［2］，因而将整个通道分为2个对向的互不影响的独立通道。

1.3 排队系统参数标定

1)乘客的到达分布。地铁直行通道内乘客的到达满足3个性质:①平稳性，即某一时间内的乘客的到达数与时间的起点无关;②后效性，即某一时间内到达n个乘客这一事件与起始时刻以前发生的事件相互独立;③普遍性，即在充分小的时间间隔内，最多有1个到达发生。所以，地铁人行通道内乘客的到达服从泊松分布P(λ)，其中:λ为平均到达率;Q为设计客流量。

2)乘客的服务时间所服从的分布。由于

通道内乘客的走行速度服从正态分布［1］N(μ，δ2)，因而服务时间的随机变量R所服从的分布为:

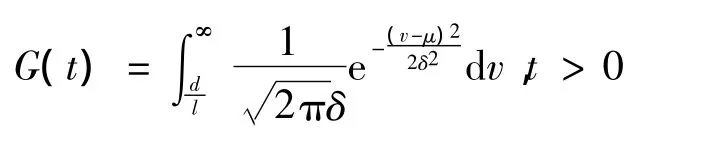
其中:d为服务窗口的直径，为常数;l为通道的长度。则服务时间的随机变量R的期望和方差分别为:

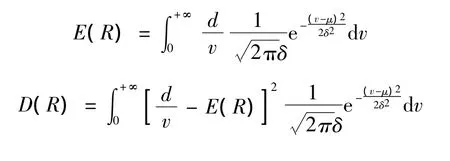
2 排队优化模型的建立与求解

2.1 模型建立

1)确定目标函数。由于双向通道宽度=［服务窗口数(c1)+服务窗口数(c2)］·服务窗口的边长(d)，而d为常量，所以所设计的满足最大客流量的最小通道宽度等价于设计最大客流量下的最小窗口数。

2)给定约束条件

①对于M/G/C模型描述的窗口，必须满足服务强度ρ小于1，否则会出现无限排队的情形，而服务强度ρ=平均服务时间E(R)/平均到达时间，平均到达时间为每个窗口的平均到达率λ/( c1+c2)的倒数，所以，

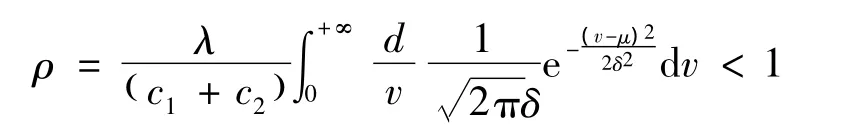
② 服务窗口数c≥1。

③通道容量限制，即平均队长不能超过通道容量。平均队长为

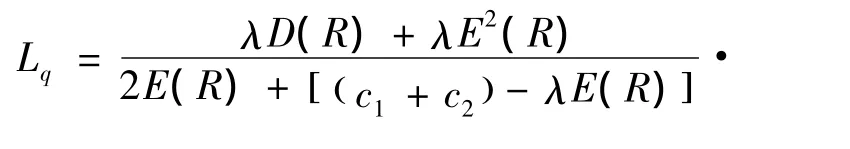
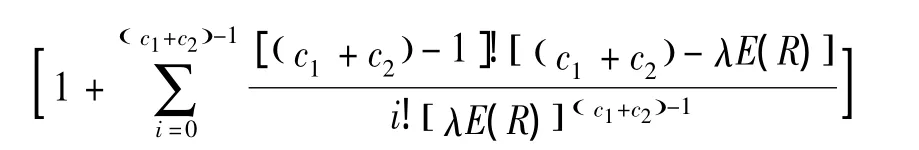
由通道的几何关系可知:( c1+c2)·Lq≤，即

3)通道排队优化模型

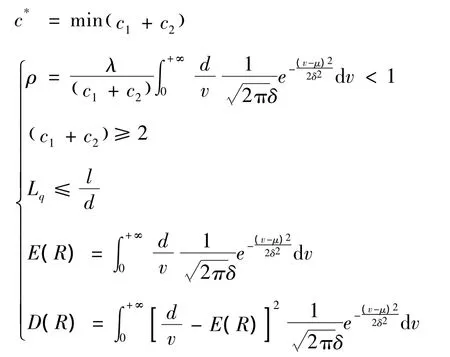
2.2 模型求解

该排队优化模型为一个非线性最优化问题，只需用Matlab软件即可求出该问题的最优解。

3 基于Simio仿真软件的模型仿真及结果分析

依据本文所给出的乘客到达和服务时间所服从的分布，建立地铁通道内的客流仿真模型，从而检验排队优化模型的有效性和正确性。

本研究以兰州市东方红广场枢纽站为例进行模型的建立和仿真。东方红广场枢纽站各年度客流预测及列车运行方案如表1所示。

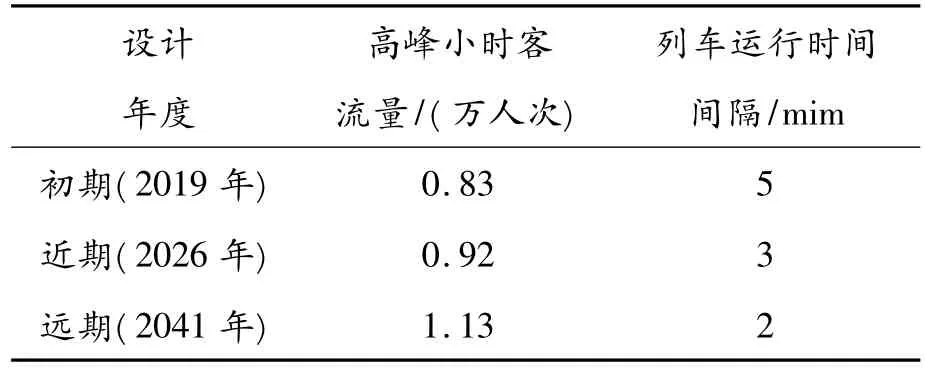
表1 东方红广场枢纽站各年度客流预测及列车运行方案

下面根据对待建枢纽站不同时期的高峰小时客流量进行预测，建立Simio仿真模型。

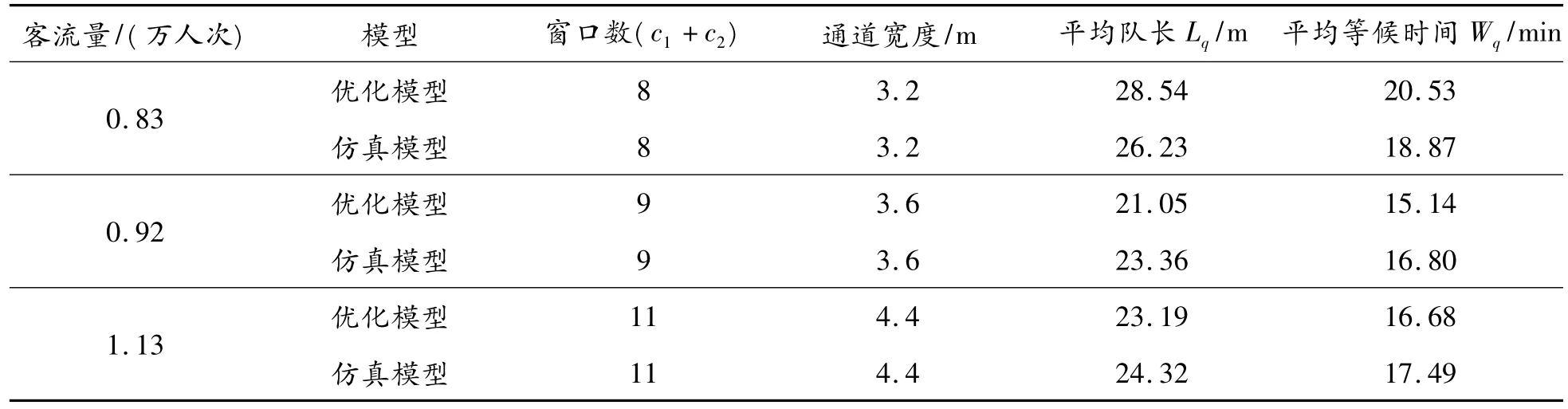
表2 不同客流量下模型参数对比

由表2可以看出，排队优化模型和仿真模型得出的结果比较接近。随着不同时期客流量的增大，通道宽度的取值也随之增大。对于同一种客流量下的不同的仿真模型，其平均排队长度和平均等候时间都基本接近，从而验证了模型的正确性。

4 结束语

本文对地铁车站直行通道行人的走行过程建立排队优化模型和仿真模型，为地铁通道的宽度设计提供了理论依据。在实际设计中，只需将相关参数带入模型计算即可。同时，此方法也可广泛的用于其他类型建筑的行人通道中，但只适用于平缓的、无坡度的直行通道中。对于楼梯，有一定坡度的行人通道中的模型，还将作进一步的研究。

［1］蒋阳升，胡路，卢果.基于排队论的地铁人行通道宽度取值方法［J］.交通运输工程学报，2010，10(3)：67-71.

［2］曹守华，袁振洲，赵丹，等.基于蚂蚁元胞自动机的地铁通道双向行人流仿真［J］.系统仿真学报，2009，21(8)：2457-2462.

［3］张晋伟，邹云，武立超.基于M/G/K排队模型的高速公路收费站设置方法研究［J］.交通标准化，2010(220)：163-166.

［4］陈绍宽，刘爽，肖熊，等.基于M/G/c/c模型的地铁车站楼梯通道疏散能力瓶颈分析［J］.铁道学报，2012，34(1)：7-12.

［5］杨涵，伍梦欢，张含笑，等.地铁换乘站不同设施区域乘客走行速度分析［J］.交通运输系统工程与息，2011，11(1)：140-145.

［6］周俊，周文正，尹平.G/M/C模型在医院口腔科门诊诊疗系统中的应用［J］.中国医院统计，2010，17(2)：135-138.

［7］纪雪艳.城市轨道交通换乘站综合评价指标体系研究［J］.铁道建筑技术，2011(5)：38-42.

［8］王扬，李盈，李旺旺.轨道交通换乘通道客流状态的信息表现形式分析及应用研究［J］.交通标准化，2011(24)：150-153.

［9］曹守华，袁振洲，张驰清，等.基于乘客感知的城市轨道交通通道服务水平划分［J］.交通运输系统工程与信息，2009，9(2)：99-104.

［10］甘应爱.运筹学［M］.3版.北京：清华大学出版社，2005.