局部化DQ法与MAPS方法的比较

唐德萍，张学莹

(河海大学理学院，南京 210098)

传统的数值解法如有限差分法(finite difference method，FDM)、有限体积法(finite volume mehod，FVM)、有限元法(finite element method，FEM)等的数值结果很大程度上取决于网格划分的质量，因此，在处理复杂几何问题以及特大变形问题时容易出现网格畸变，严重影响解的精度，甚至导致计算失效。为了克服以上缺陷，无网格方法应运而生。在众多的无网格方法中基于径向基函数(radial basis functions，RBFs)的无网格法备受瞩目。20世纪60年代 Hardy［1］成功地将多重二次函数(multiquarics，MQ)应用于拟合散步数据问题。20世纪90年代Kansa［2-3］首次提出利用RBFs求解偏微分方程的思想。不过这些方法中的RBFs具备全局性质，因此，由它所形成的系数矩阵是满阵，有时甚至是很病态的，这给处理大规模问题带来了诸多的不便。为了改进这些方法，区域分解法［4］、多重网格法［5］等相继问世。之后，研究者们将目光转向局部化的无网格方法［6-8］，特别是Shu C等［6］的局部微积分法(local radial basis-functioned differential quadrature，LRBF-DQ)和Chen C S等［7］的局部近似特殊解法(local method of approximate particular solution，LMAPS)。这2种方法不仅操作起来灵活方便，而且还能保证精度方面的要求。鉴于这2种方法的相似性，本文将对这2种方法进行比较研究，并给出误差分析。

1 2种基于RBFs的无网格方法

1.1 局部RBF-DQ方法

设f(x)是光滑函数，其中x=(x1，x2，…，xn)T。已知它在结点xi及其支撑域内各支撑点xj，j=1，…，ni上的函数值，则f(x)关于xk的m阶导数可以表示为

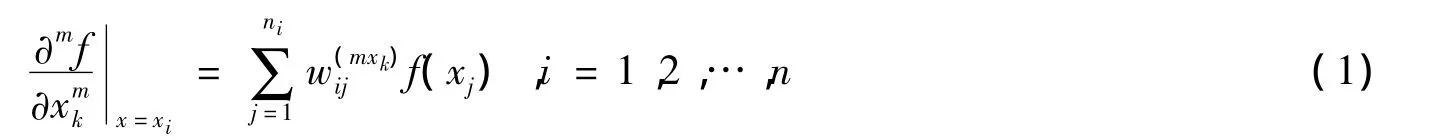
其中:xk表示第k个坐标方向表示线性组合系数。将径向基函数φ代入方程(1)中，得到

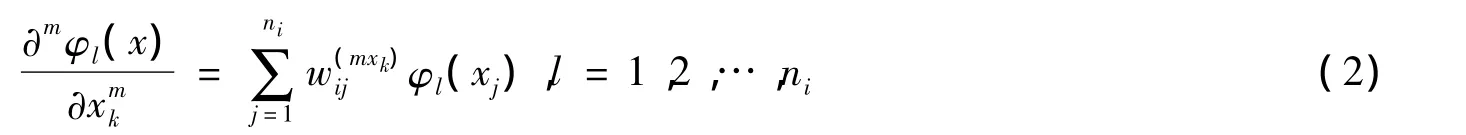
这里φl(x)=φ(‖x-xl‖)。式(2)还可以化为如下形式:

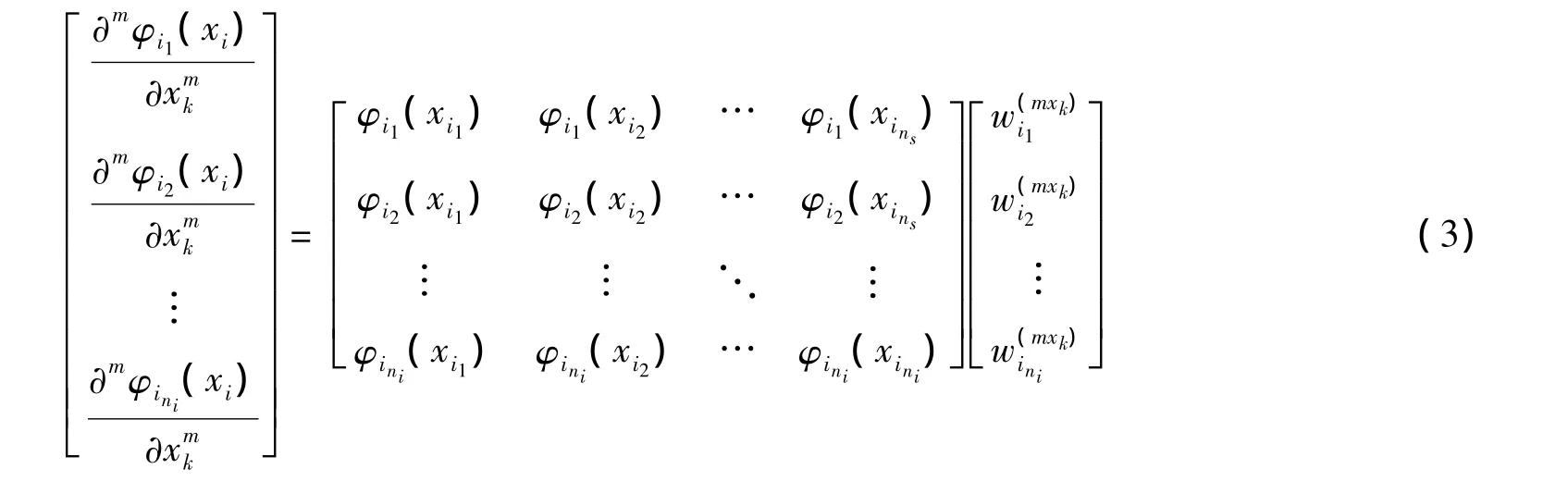
由文献［9］知式(3)中的系数矩阵是条件正定的，故系数矩阵可逆，从而可以求出系数，将之代入式(1)就可以求出函数f关于xk的m阶导数的近似值。

1.2 局部MAPS方法

由特别解法［10-11］知，u(xi，yi)可以由 ni个 RBFs的线性组合近似:

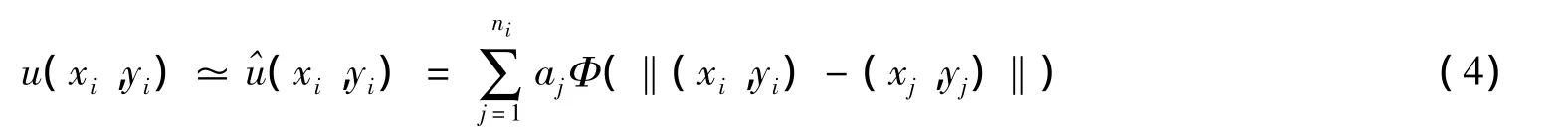
1.3 方程的求解过程

全文选取MQ函数作为基函数，它的表达式为

目前，野生动物栖息地的保护已经成为一项非常重要的任务，为了让各类野生动物有一个美好的家园，人们应该正确树立保护野生动物的思想意识，不乱砍乱伐，不肆意杀戮，确保野生动物的生存与繁衍。同时，国家应该加大对野生动物栖息地的保护力度，安排相关人员在野生动物保护区坚守岗地，在未经允许的情况下，禁止任何人进入野生动物保护区，并且倡导周边的人民群众一起做好保护野生动物的工作。

其中c是形状参数。2种方法的求解过程为:①确定求解区域点的分布以及支撑域中内点的数量;② 计算组合系数;③利用上一步中已经求得的系数去离散偏微分方程;④求解离散化的偏微分方程。

考虑如下边界值问题:

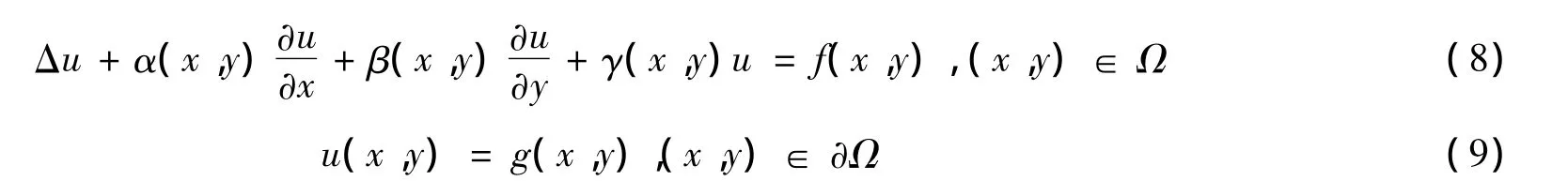
其中:Δ 是 线性二阶线性 L aplace 算子;α(x，y)、β(x，y)、γ(x，y)、f(x，y)和 g (x，y)是给定的函数。设{ ( xj，yj)}是区域 Ω 内 的插值点，∀(xi，yi)∈Ω，构建一个支撑区域 Ωi，{ ( xj，yj)}是与(xi，yi)相邻的ni个点，且 { ( xj，yj)}⊂Ωi。用局部DQ法离散方程(8)和(9)，得

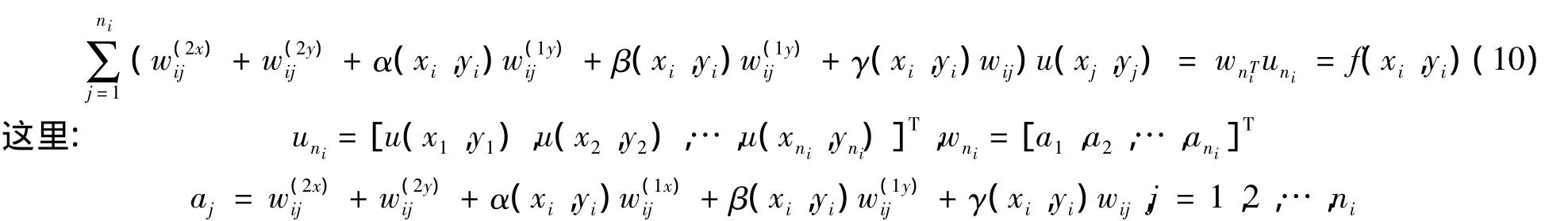
若( xi，yi)⊂∂Ω，则有

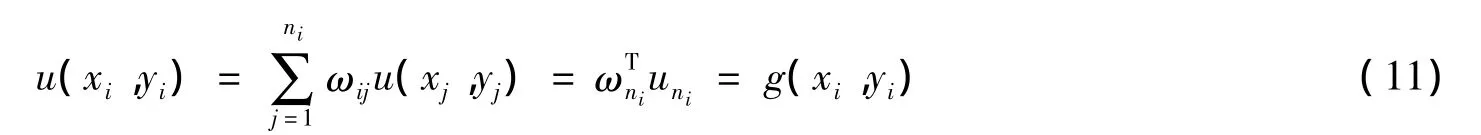
其中 ωni=［ωi1，ωi2，…，ωini］T。

通过在适当位置添加零元素将wni从局部形式推广至全局形式，即将向量wni延拓至n维向量wn，其中有n-ni个零元素，详细的延拓方法参见文献［7］。从而得到:

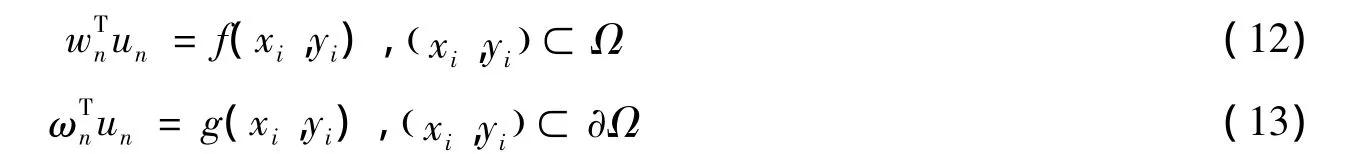
用局部MAPS方法离散方程(8)和(9)得

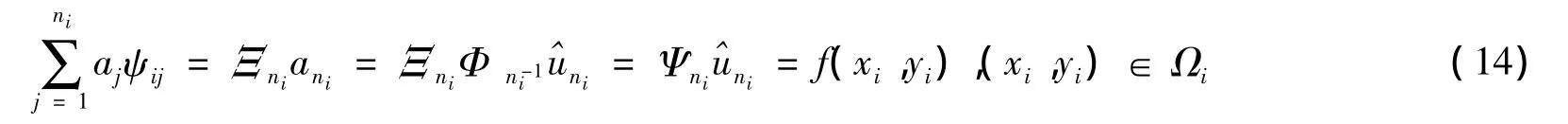
其中:

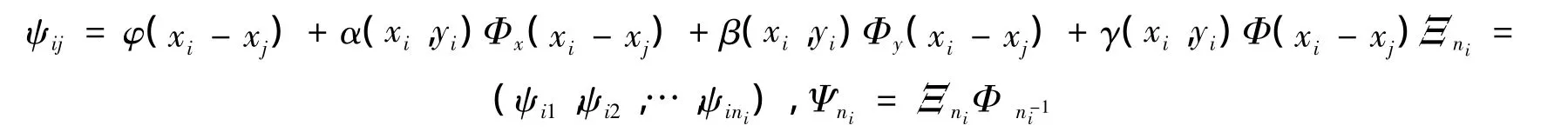
至于将局部形式推广成全局形式采用与局部DQ方法的做法，本文就不做赘述。

2 数值算例

本文考虑均方根误差(RMSE)、最大绝对误差(MAE)、最大相对误差(RAE)。它们的定义为:

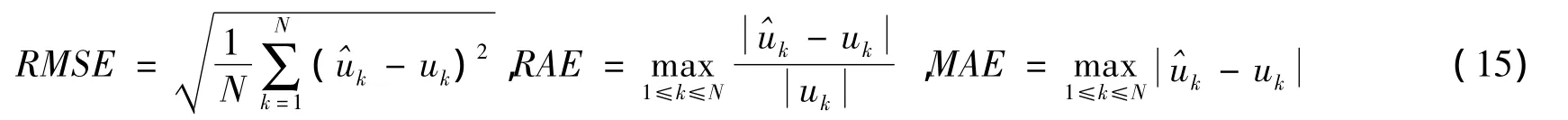
算例1 首先考虑二维Possion方程

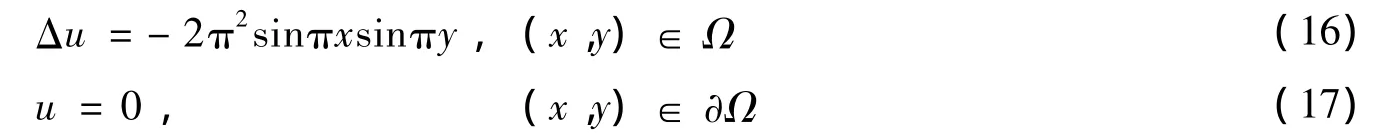
其中 Ω∪∂Ω =［0，1］2。问题的精确解为 u(x，y)=sinπxsinπy。

图1是LRBF-DQ和LMAPS在不同网格尺寸下关于形状参数c的数值结果。观察此图，可以惊奇地发现:LMAPS法在c=m时，形状参数都趋于稳定，而LRBF-DQ法则在此时取得最优值。因而不必担心c的取值，只要取c=m即可。表1则清晰地表明，无论应用哪种方法，所取得的数值结果都比较令人满意，并且随着插值点的增加，所取得的数值结果的计算精度越来越高。

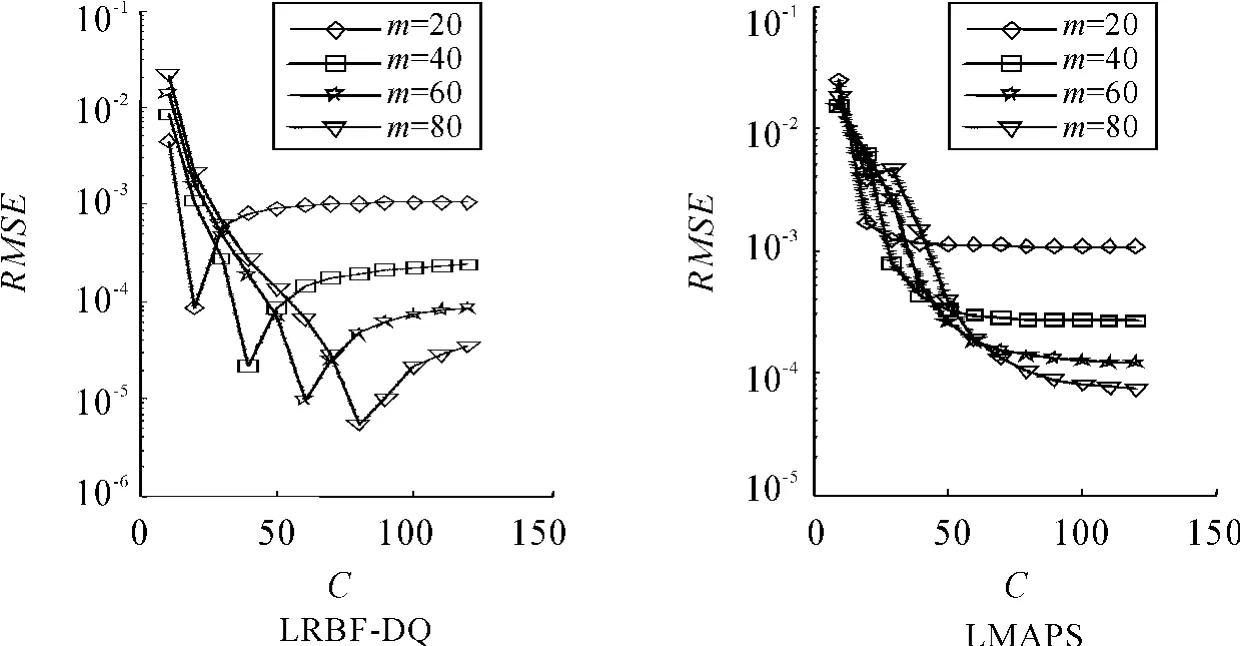
图1 LRBF-DQ和LMAPS在不同网格尺寸下关于形状参数c的数值结果

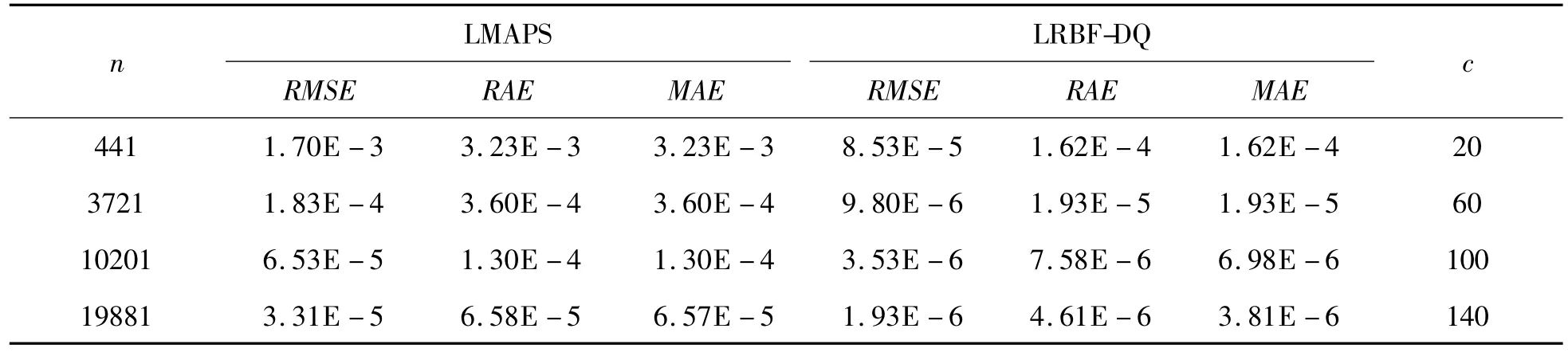
表1 对于不同插值点应用LMAPS和LRBF-DQ方法的数值结果

算例2 考虑不规则区域下的Possion方程问题:

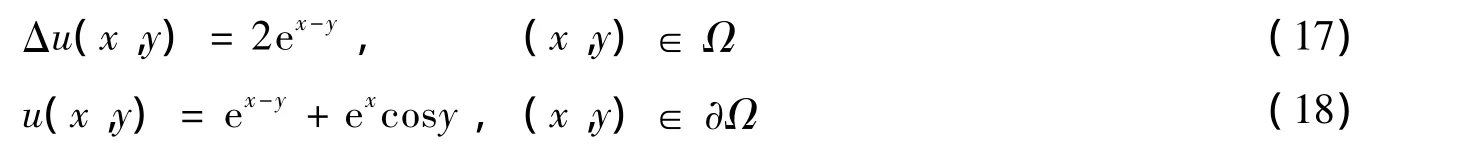
其边界是一个星型的区域，具体的表达式为

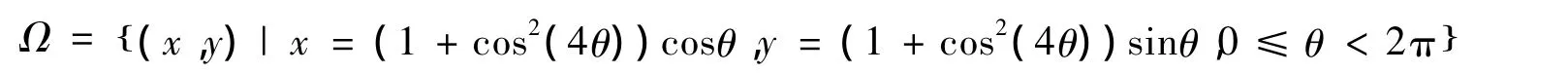
计算区域如图2所示。图3表明，这2种方法在整个不规则计算区域上的相对误差都是平滑下降的，只是在星型图形各角处的误差有跳跃现象。另外，2种方法的计算精度都比较高，局部MAPS法的相对误差甚至可以达到10-6。

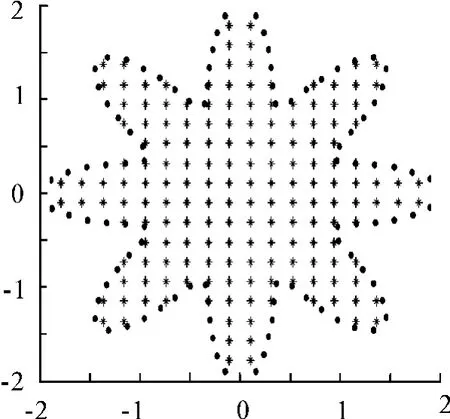
图2 不规则区域下的Possion问题的计算区域

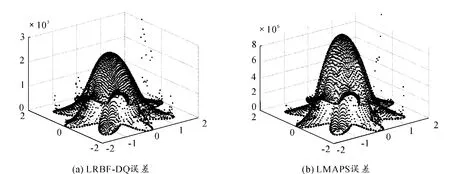
图3 nb=200，ns=3 676时局部RBF-DQ法与局部MAPS法得到的相对误差对比

表2为LRBF-DQ法与LMAPS法的误差对比，它清晰地表明，无论哪种方法，随着插值点的增加，计算结果的精度也越来越高，而且后者的计算速度比前者更快。不管从精度还是从计算速度上来看，LMAPS法都比LRBF-DQ法略有优势。

表2 LRBF-DQ法与LMAPS法数值结果的误差对比

3 结束语

本文主要介绍了LMAPS和LRBF-DQ这2种方法，它们都具有真无网格性质，而且特别适用于解决高维问题。LRBF-DQ利用DQ法直接近似场量导数，再用RBFs来近似函数。整个过程中，LRBF-DQ法需要求出各个坐标方向上函数偏导数的线性组合系数，而LMAPS则是利用RBFs的特别解近似问题的数值解。本文选择难以处理的不规则计算区域上的Possion方程问题来比较LMAPS和LRBF-DQ方法。实验结果表明:这2种基于RBFs的无网格方法计算效率都比较高，且能保证精度方面的要求。

［1］Hardy R L.Multiquadric equations of topolography and other irregular surfaces［J］.J Geophysics Res，1971，176：1905-1915.

［2］Kansa E J.Multiquadrics-a scattered data approximation scheme with applications to comutational fluid-dynamics.I.Surface approximations and partial derivative estimates［J］.Comput Math Appl，1990，19：127-45.

［3］Kansa E J.Multiquadrics-a scattered data approximation scheme with applications to computational fluid-dynamics.II.Solutions to parabolic，hyperbolic and elliptic partialdifferential equations［J］.Comput Math Appl，2000，39：123-37.

［4］Beatson R K，Greengard L.A short course on fast multipole methods［M］//Ainsworth M，Levesley J，Light W，et al.Wavelets，Multilevel Methods and Elliplic PDEs.Oxford ：Oxford University Press，1997：1-37.

［5］Chen C S，Golberg M A，Ganesh M，et al.Multilevel compact radial functions based computational schemes for some elliptic problems［J］.Computers and Mathematics with Application，2002，43：359-378.

［6］Shu C，Ding H，Yeo K S.Local radial basis function-based differential quadrature method and its application to solve two-dimentional incompressible Navier-Stokes equations［J］.Comput Methods Appl Mech Eng，2003，192：941-954.

［7］Yao G M，Chen C S，Joseph Kolibal，A localized approach for the method of approximate particular solutions［J］.Computers and Mathematics with Applications，2011，61：2376-2387.

［8］Divo E ，Kassab A J.An efficient localized rbf meshless method for fluid flow and conjugate hear transfer［J］.ASME Journal of Heat Transfer，2007，129：124-136.

［9］Micchelli C A.Interolation of scattered data：distance matrices and conditionally positive definite functions［J］.Constr Approx，1986(2)：11-22.

［10］Chen C S，Fan C M，Wen P H.The method of particular solutions for solving certain partial differential equations［J］.Numerical Methods of Partial Differential Equations，2012，28：506-522.

［11］Chen C S，Fan C M，Wen P H.The method of particular solutions for solving elliptic problems with variable coefficients［J］.International Journal of Computational Methods，2011(8)：545-559.