“假设检验”决策的误区——一场由全国大学生数学建模竞赛引发的争论

易昆南，程勋杰

(中南大学数学与统计学院，长沙 410075)

1 问题的提出

问题1［1］是这样提出的:分析附件1中 A、B两组评酒员对27组酒样的评价结果有无显著性差异，哪一组结果更可信?

2 方差分析法

方差分析法解法思路:取A、B两组评酒员对27组酒样打分的平均值(或打分之和)作单因素方差分析，用检验结果来判断两组评酒员对27组酒样的评价结果有无显著性差异。

方差分析［2］(analysis of variance，ANOVA)又称“变异数分析”或“F检验”，是由 R.A.Fisher发明的，用于对两个及两个以上样本均数差别的显著性检验。对于给定的显著性水平α∈ (0 ，1)，若p=P{ F ≥F0}＜α，则拒绝原假设H0(F0为F统计量的观测值)，可以认为所考虑的因素对相应变量有显著性影响;否则，不能拒绝H0，认为所考虑的因素对相应变量无显著性影响。

方差分析的最重要的假定条件为:①各处理条件下的样本是相互独立的，否则可能出现无法解析的输出结果;② 各处理条件下的样本分别来自正态分布总体，否则使用非参数分析;③各处理条件下的样本方差相同，即具有齐效性。

假设条件①、②容易得到满足，而假设条件③恰恰是不满足的!通过对题目提供的红葡萄酒、白葡萄各27种样本数据的计算，在显著性水平α=0.05下，两总体的方差都有显著性差异(例如对红葡萄酒的计算，在方差是否相等的检验检验中，第1组样本方差=53.91，第2组样本方差=15.82，F=3.14，p 值为 0.002 6，检验结果认为两正态总体方差不等)。所以直接由上述方法得出的结论是一种很糟糕的结果。

另一种处理方法:按每一种酒样(共27个酒样)，对两组评酒员的打分结果做单因素方差分析，这样可以得到相应的结果，见表1。

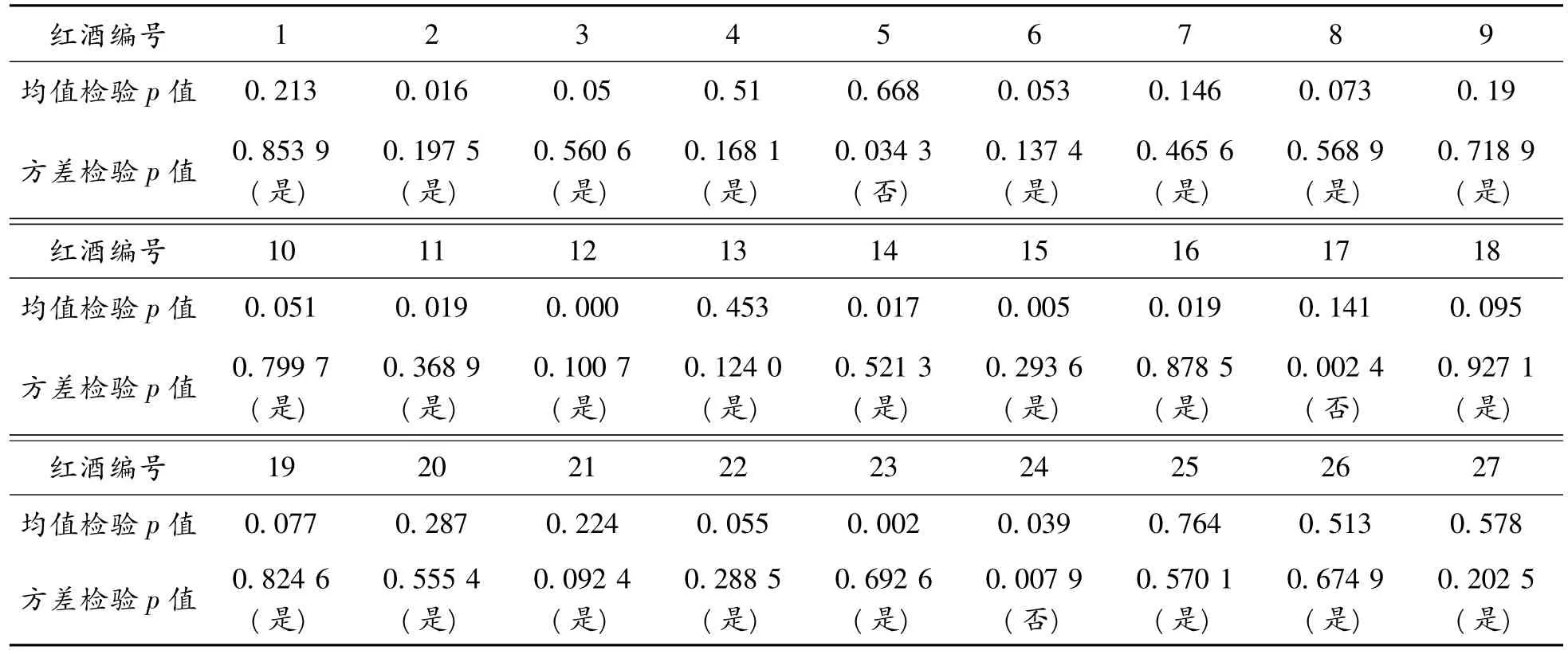
表1 27个酒样的两组评酒员打分的方差分析结果(α=0.05)

在27个酒样对应的两组样本的方差分析中，当水平α=0.05时，仍有3个不满足方差齐性的要求(见表1中黑体数字)。

即使27个酒样对应的两个总体都满足方差齐性，分析表1中的数据，发现大于显著性水平的数值共有19个，也就是说给定α=0.05，27种红葡萄酒评价结果中可以认为无显著性差异的结果所占的比例为，由此可以认定在给定α=0.05水平下，以0.704的概率接受，两组评酒员的评价结果无显著性差异。

但是当改变一下显著性水平α的值，比如取α=0.06时，可以发现大于0.06的结果共有11个，那么无显著性差异的结果所占的比例为40.7%，和α=0.05相比，比例直接下降了将近30百分点。对两组评酒员的评价结果无显著性差异越来越缺乏自信。

通过上面的分析可以得出，应用上述方差分析的方法(且不说未检验两组样本的方差齐性!)作出判断的关键变成了α的选取，当α取的较小时(如α≤0.05)，得出的结果是两组评价结果之间没有显著性差异，当α取的稍微有些大时(如α=0.06)，则得出的结果就是两组评价结果之间有显著性差异!

事实上，假设检验难免要犯错误，假设犯第1类错误［3］的概率为α=0.05，并假设27次检验都是独立进行的，正确接收全部原假设的概率为(1-α)27=0.9527≈7.45 ×10-36，概率几乎为 0，错误的拒绝其中至少一个假设的概率为1-(1-0.05)27，几乎为1。虽然这种方法看似比第1种方法更合乎逻辑，但实质上解法也是错误的。

用单因素方差分析处理两组评酒员对27组酒样的评价结果有无显著性差异的问题，实质上是两个正态总体的方差相等条件下的均值是否相同的检验问题，方差分析与t检验的方法等价。问题的关键在于:27组酒样有着自身的质量排名，A组10人对每一酒样打分的平均分所得到的27个样本不能看作取自同一总体N(μ1，σ2)的样本;同样来自B组的27个样本不能看做取自同一总体N(μ2，σ2)的样本。即使方差齐性满足，无论使用这两种方法中的哪一种，样本中都参杂了27组酒样的差异，无法保证得到正确的结论。

3 配对t检验

两独立样本 t检验［4，6］就是根据样本数据对两个配对样本来自的两总体的均值是否有显著性差异进行推断。

两配对样本t检验的前提条件:① 需要克服试验因素带来的干扰，否则无法区分结果的差异究竟是两总体均值的差异还是试验因素带来的差异;②样本来自的两个总体应该服从正态分布，或配对数据之差服从正态分布。

以白葡萄酒为例，设来自A组28个样本与B组28个样本的配对数据之差为取自“两组对白葡萄酒评价的差异”这一总体的简单随机样本，假设这个总体服从正态分布 N(μ，σ2)，μ，σ2均未知，检验假设H0:μ=0，若拒绝原假设，则认为两组对白葡萄酒评价有显著性差异。注意:不要设“A组对白葡萄酒的评分”为一正态总体N(μ1，σ2)，A组28个样本为取自该总体的样本，前面已经提及，这种提法本身是有问题的。

用配对t检验方法步骤:① 检验配对数据之差服从正态分布;② 进行两正态总体均值是否相同的配对t检验。

具体检验如下(以白葡萄酒为例)。

首先通过计算两组白葡萄酒配对样本的差值，继而计算对应的均值、方差，做正态分布的拟合检验。整个计算可通过 SPSS 19.0来完成［5］。检验结果见表2。

表2 拟合检验结果

检验结果符合正态性假设。配对数据之差的P-P图见图1。

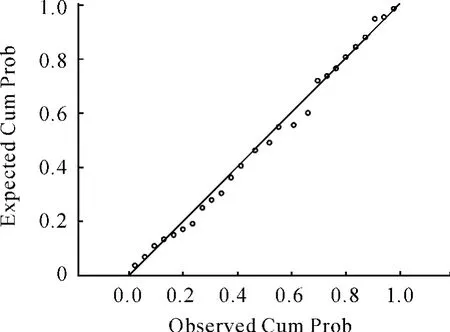
图1 配对数据之差的P-P图

从图1中可以发现，数据分布在直线附近。P-P图同时也是对上述结论的佐证，因此可以用配对t检验进行求解。得到的结果见表3。

从表3中可以看到概率p值等于0.038，小于0.05，故认为两组评酒员的评价结果有显著性差异。对红葡萄酒进行类似的分析，得到的结果见表4。

表4中概率 p值为0.021，也小于0.05。

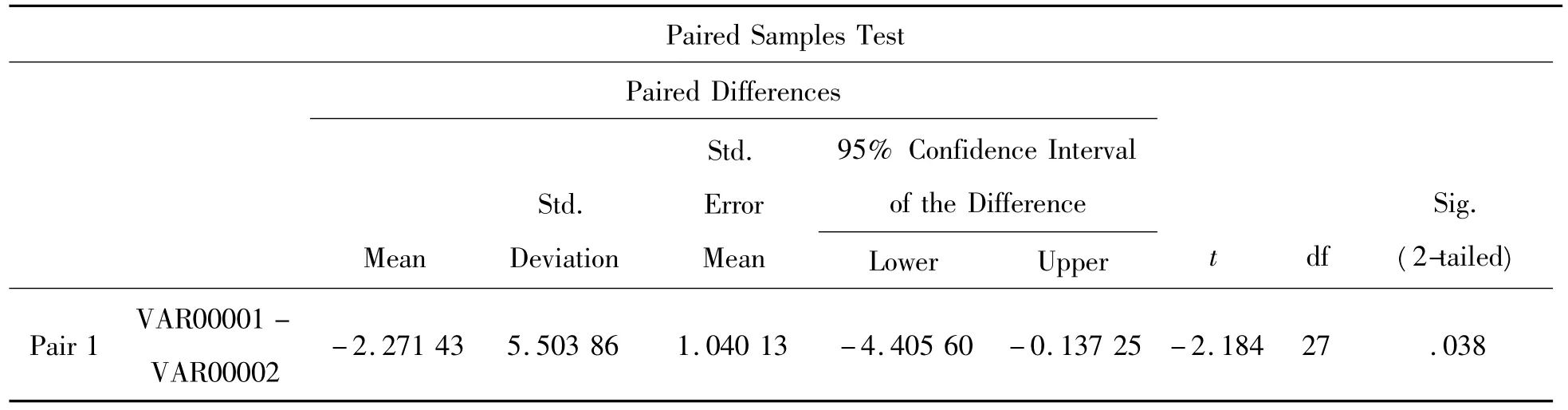
表3 白葡萄酒配对t检验结果

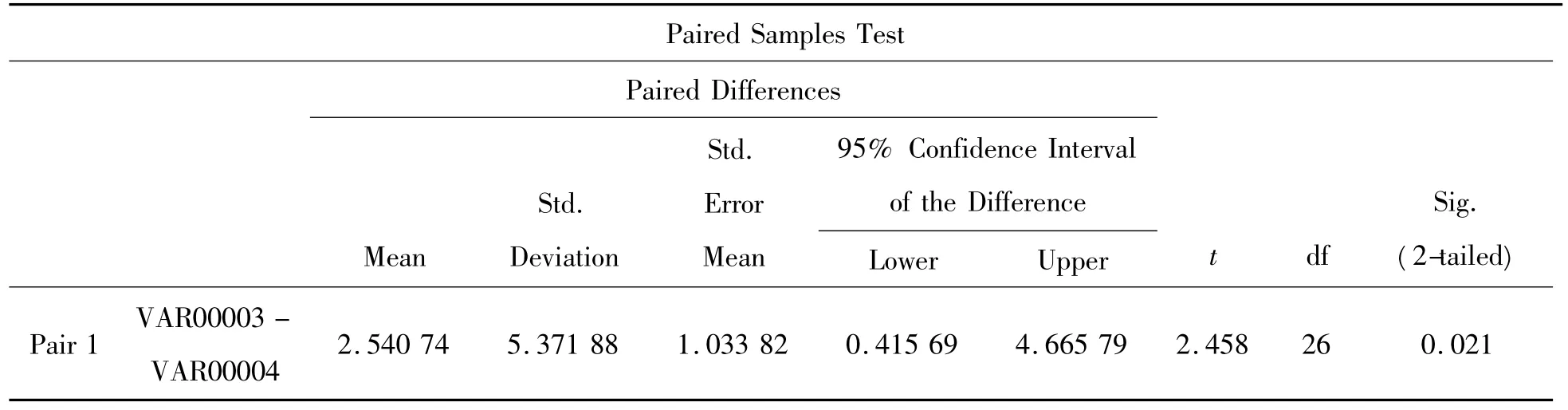
表4 红葡萄酒配对t检验结果

两次检验结果都表明:两组评酒员的评价结果之间存在显著性的差异，所以有理由相信两组评酒员的评价结果是存在显著性差异的。

4 结束语

在讨论哪一组结果更可信时，有的参赛队以哪一组评酒打分方差最小来简单选择哪一组结果更可信，其实方差小只能说明该组对问题的看法比较一致，只能从一个侧面说明问题，但该组打分可能存在系统的偏差(即该组打分与真实排名的差距)，这可能是更重要、更要命的问题，处理的常见方法有字典序法［7-9］等。

统计分析方法繁多，只有充分认识问题是否满足该统计分析方法的条件时，才能正确地使用该统计分析方法，这是在前期的数学建模培训中特别要注意的。

［1］2012年全国大学生数学建模竞赛试题［EB/OL］.http：//ishare.iask.sina.com.cn/f/33790432.html.

［2］何晓群，刘文卿.应用回归分析［M］.北京：人民大学出版社，2007.

［3］魏宗舒.概率论与数理统计教程［M］.北京：高等教育出版社，2009.

［4］膝龙.包其郁.配对t检验误区与率转化配对t检验方法介绍及各自应用范围［J］.医学研究通讯，2003，32(7)：21-23.

［5］杜强，贾丽燕.SPSS从入门到精通［M］.北京：人民邮电出版社，2011.

［6］陈佩珍，陆守曾.关于配对t检验效能的研究［J］.中国卫生统计，1996，13(6)：19-22.

［7］司守奎，孙玺菁.数学建模算法与应用［M］.北京：国防工业出版社，2011.

［8］明日科技 .Visual C++从入门到精通［M］.北京：清华大学出版社，2012.

［9］龚纯，王正林.MATLAB语言常用算法程序集［M］.北京：电子工业出版社，2008.