平衡损失函数下具有时间变化效应的信度保费
2013-07-06李新鹏吴黎军
李新鹏,吴黎军
(新疆大学数学与系统科学学院,乌鲁木齐 830046)
1 预备知识
在保险实际应用中,精算师的一个重要任务之一就是对给定的风险制定一个合适的保费。现代信度理论起源于Bühlmann[1]得到了任意分布下的净保费信度估计。信度理论是基于过去的索赔经历来制定保费的一种定量方法。信度保费为样本均值和聚合保费的加权和,其中权重因子又被称为信度因子。
令Xi表示保单持有人在第i个保单时期的索赔额,Xi的分布依赖于风险参数Θ。由于风险的非其次性,一般假设Θ是随机变量,具有先验分布为 π(θ),若给定 Θ =θ,Xi(i=1,2…n)相互独立,且有相同的分布函数F(x,θ)。信度理论的目的是在给定保单持有人的前n个时期根据索赔经历来计算第n+1个时期的保费。如果将估计限定在索赔额的线性函数中,则得到著名的信度公式:
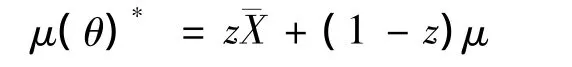
其中:z=n/(n+k)为信度因子;k为条件方差的期望值与条件期望的方差值的比值;为样本均值;μ为聚合保费。
经典的信度理论中假定不同年份的索赔序列有共同的风险参数,在风险参数给定时,各年的索赔相互独立,且具有相同的分布,没有考虑不同年份之间风险的时间效应。温利民等[2]在均方损失函数下研究了各年索赔风险间具有时间变化效应的信度模型,得到了相应的信度保费。考虑时间方面相依性的信度模型与实际情况更为符合。温利民等在2009年研究了各年索赔风险间具有等相关的信度模型,得到了相应的信度保费。Bolancé等[3]建立了索赔频率风险模型,得到了时间效应为自相关时间序列时的信度保费。Purcaru与Denuit[4]在 Poisson索赔频率风险模型中讨论了相依结构对信度估计的影响。Frees等[5]研究了时间效应为Student-t copula时的信度保费。
经典的决策论中,损失函数的选择通常取决于估计的精确性,然而,拟合的好坏也是一个重要的标准。Zellner[6]引入了平衡损失函数的概念,它既反映了好的拟合度又反映了估计的精确性,函数如下:
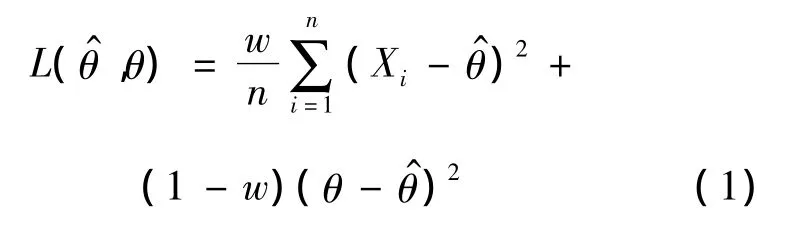
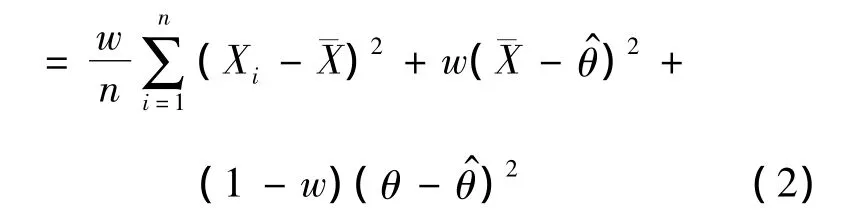
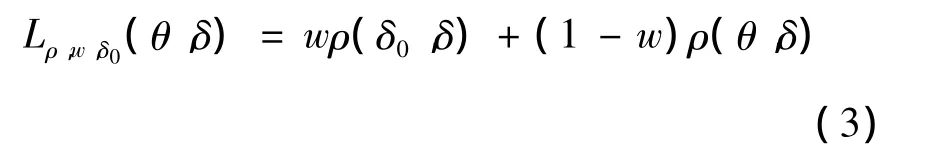
其中:ρ为距离函数;δ0为目标估计,它通常由极大似然估计、最小二乘法或者无偏性条件获得;δ为θ的估计值;距离函数通常选为均方误差损失函数。
本文在平衡损失函数下考虑了具有时间变化效应的信度模型,并且得到了相应的信度保费[7-10]。
2 模型假设与准备
在信度理论中,假设保单组合的风险参数为Θ,且有n年的索赔额,由于风险的非齐次性,风险参数Θ假定为随机变量。本文的目标为预测保单在未来1年的索赔Xn+1。但与经典的信度理论不同,本文假设在风险参数给定的条件下,索赔随机变量 X1,X2,…,Xn有各自的风险参数 Θ1,Θ2,…,Θn,且这些风险参数具有某种相依结构。模型的基本假设如下:
假设1 给定时间变化效应Θi=θi时,索赔额 Xi,i=1,…,n 互相独立且同分布 E(Xi|Θi)=μ(Θi),Var(Xi|Θi)=σ2(Θi),i=1,2,…,n。
假设2 风险参数Θi的分布函数为πi(θ),且 E[μ(Θi)]=μ,E[σ2(Θi)]=和协方差Cov[μ(Θi),μ(Θj)]= τiτj.i,j=1,…n。
假设3 本文中平衡损失函数为:
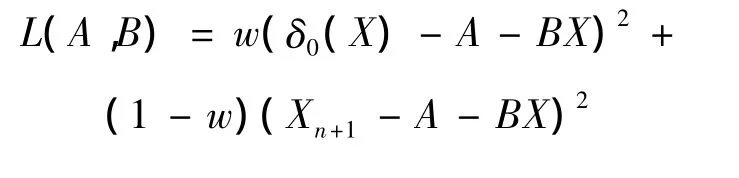
其中 δ0(X)为目标估计,X=(X1,…,Xn)'且E[δ0(X)]= μδ,Cov[δ0(X),Xi]=di,i=1,2,…,n,w为权重因子。
本文目标为求解下面最优化问题:
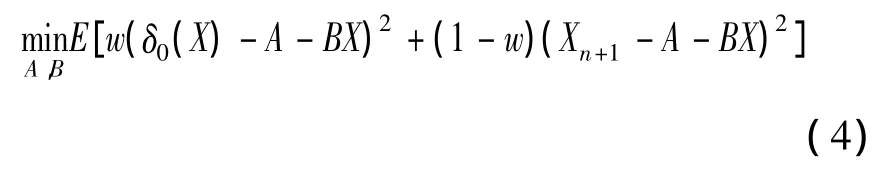
为求解最优化问题(4),记L(X,1)={a0+
引理1~3[2]表明了相依结构的一些简单但重要的性质。
引理1 在假设1和假设2下,有:
①Xi的均值为
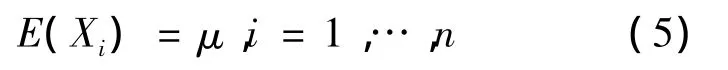
②过去索赔和未来索赔的协方差为
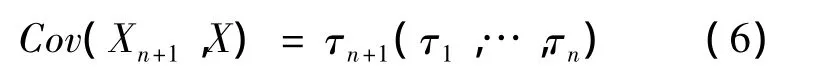
③X的协方差矩阵为
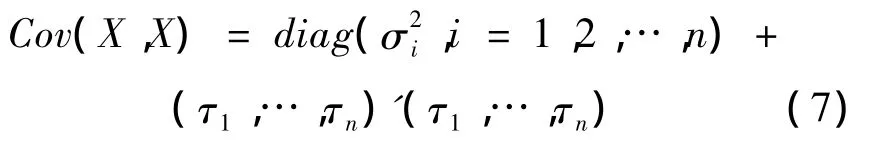
其中diag[…]为对角矩阵。
④X的协方差矩阵的逆为
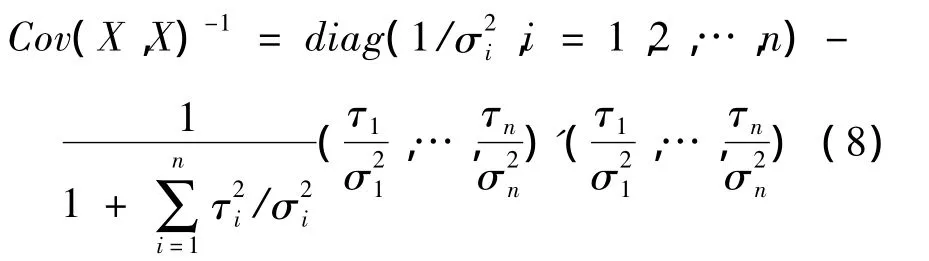
引理2 假设(X'1×p,Y'1×q)'为一随机向量,期望和协方差矩阵分别为(μ'X,μ'Y)和则当时,期望损失E(Y-A-BX)'(Y-A-BX)达到最小。
引理3 风险Xn+1的非齐次信度估计为Xn+1在L(X,1)上的正交投影,即
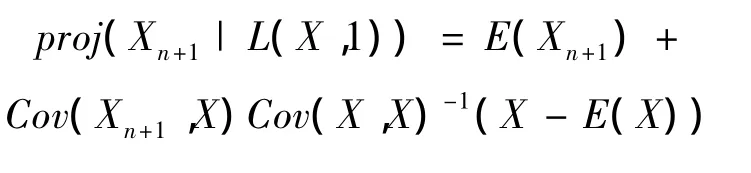
3 平衡损失函数下的信度估计
定理1为最优化问题(4)的解,即未来索赔Xn+1的信度保费。
定理1 在假设1~3下,运用平衡损失函数,Xn+1的最优线性非齐次估计为
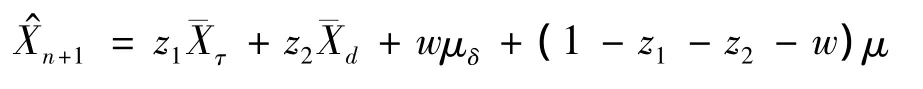
其中:
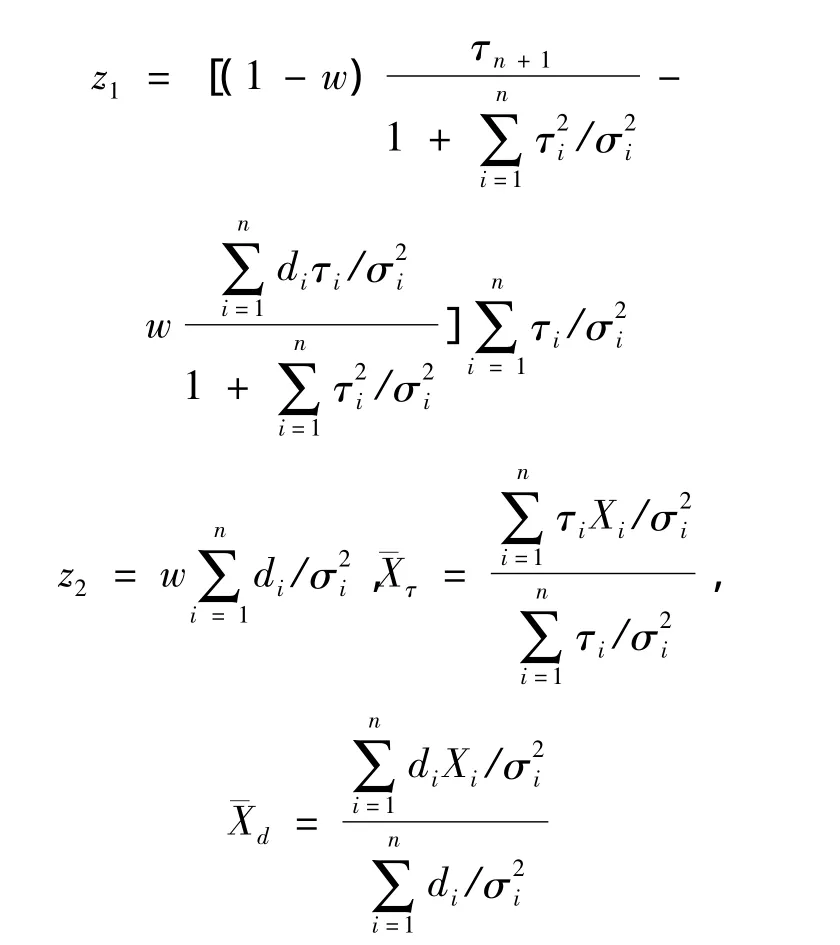
证明引入一随机变量Y=Iδ0(X)+(1-I)Xn+1,其中I为0-1随机变量,它独立于其他的随机变量,并且P(I=1)=1-P(I=0)=w,w为式(4)中的权重因子。因此,最优化问题(4)等价于
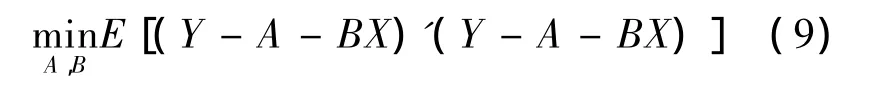
由引理2和引理3知,下一年保费的最优估计为
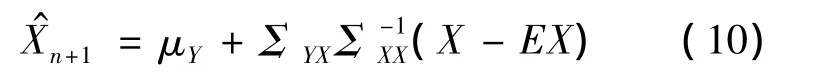
根据Y的定义,均值μY为:
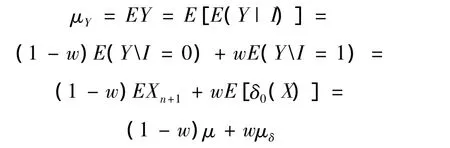
又因为E(XI)=E(X)为一常数,所以
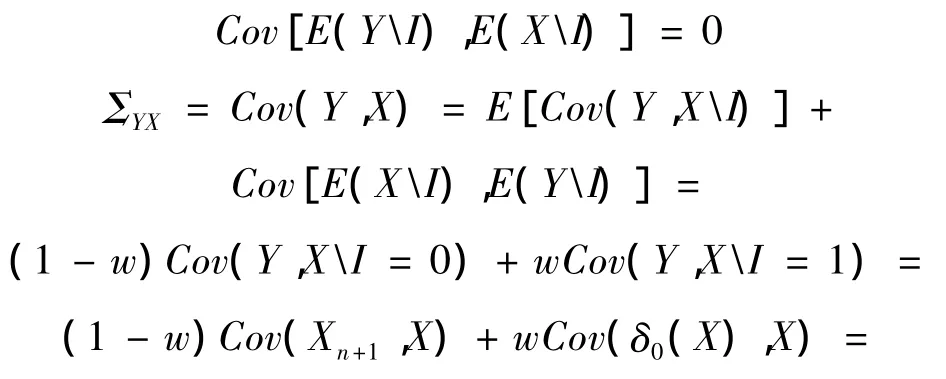
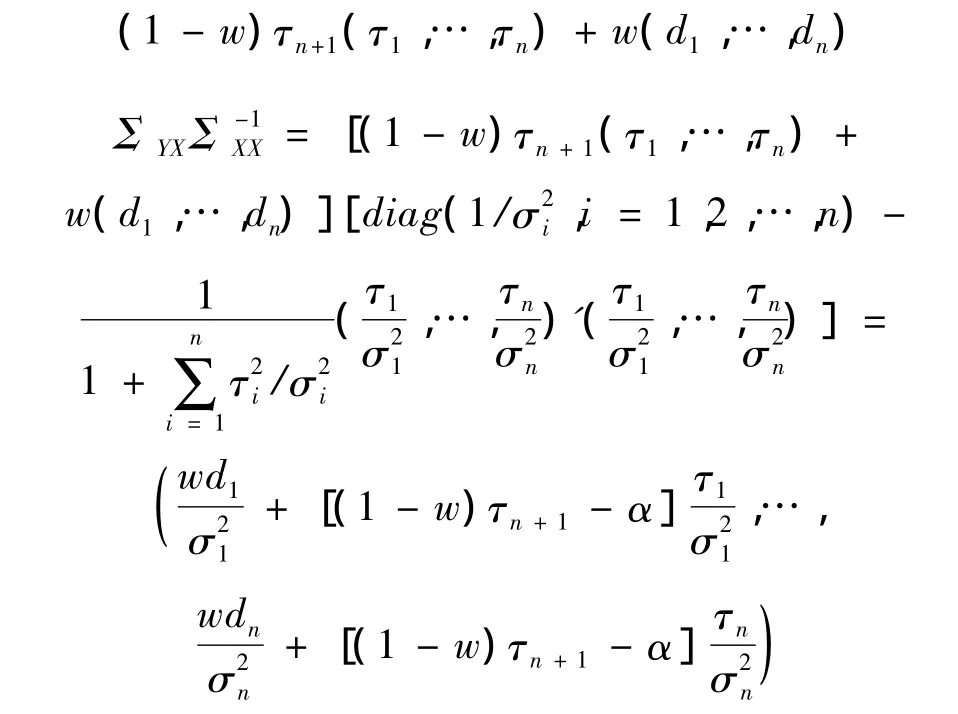
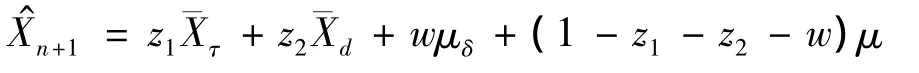
定理得证。
注1 当w=0时,此定理给出的保费与温利民等在2012年提出的具有时间变化效应信度模型的保费一致。
4 Bühlmann-Straub模型的信度估计
本节将给出在平衡损失函数下具有时间变化效应的Bühlmann-Straub信度模型的保费。将假设1中的Var(Xi|Θi)=σ2(Θi)改为 Var(Xi|Θi)=σ2(Θi)/mi,i=1,2,…,n,mi为 Xi自然权重因子,其他假设不变。
引理4 在本文第3节的假设和上面的假设下,有以下结果:
①Xi的均值为
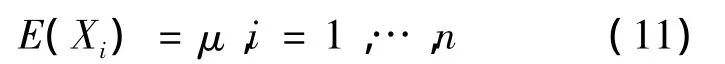
②过去索赔和未来索赔的协方差为
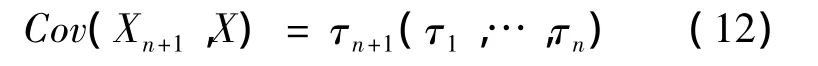
③X的协方差矩阵为
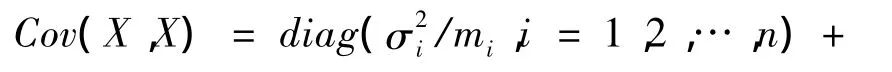
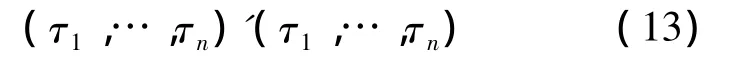
其中diag[…]为对角矩阵。
④X的协方差矩阵的逆为
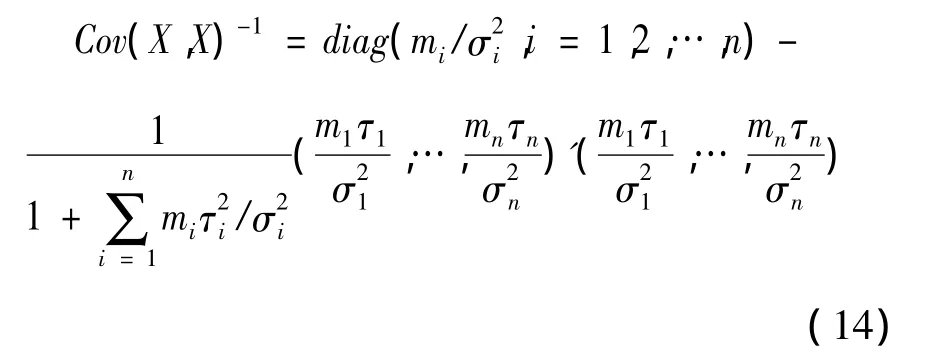
定理2 在本文第3节假设和本节假设下,运用平衡损失函数,Xn+1的最优线性非齐次估计为
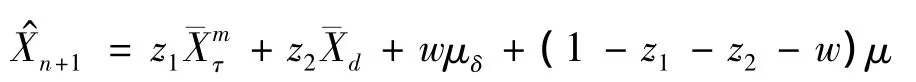
其中:
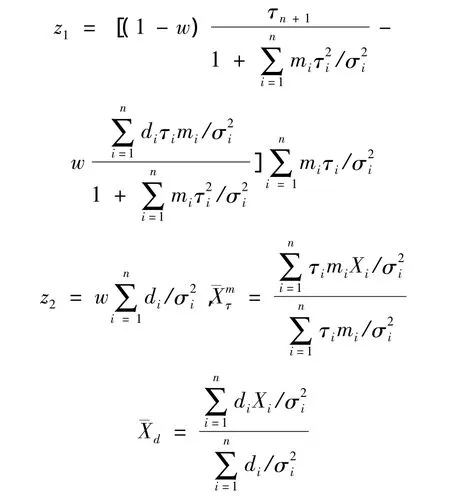
定理2的证明与定理1的证明类似,所以只给出粗略的证明。
证明引入一随机变量Y=Iδ0(X)+(1-I)·Xn+1,其中I为0~1随机变量,它独立于其他的随机变量,并且P(I=1)=1-P(I=0)=w,w为式(4)中的权重因子。因此,最优化问题(4)等价于
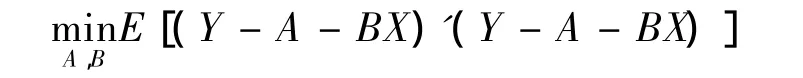
由引理2和引理3知:下一年保费的最优估计为
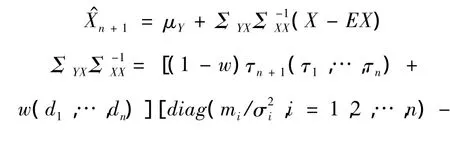
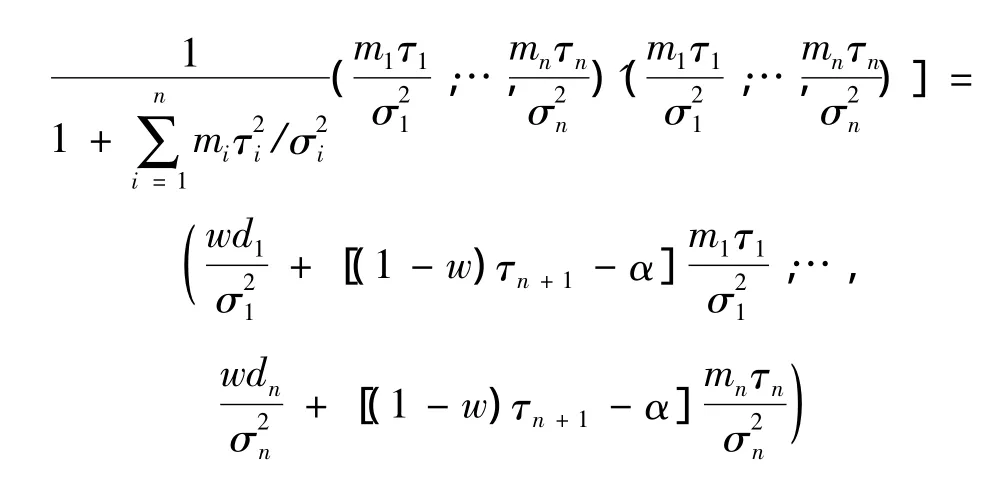
其中
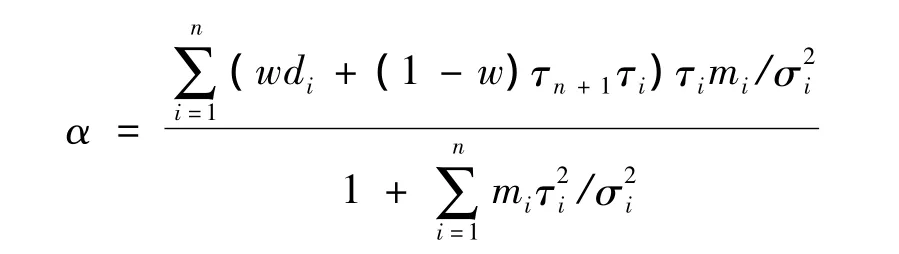
所以,下一年最优非齐次信度保费为
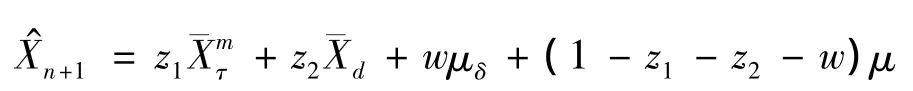
5 结束语
本文运用平衡损失函数,研究了具有时间变化效应的Bühlmann和Bühlmann-Straub信度模型的保费估计问题,并且推导出相应的信度保费,但是对于参数的估计还需今后深入研究。
[1]Bühlmann H,Gisler A.A course in credibility theory and its applications[M].Netherlands:Springer,2005:77-264.
[2]温利民,郑丹,章溢.具有时间变化效应的信度模型[J].江西师范大学学报:自然科学版,2012,36(3):249-252.
[3]Bolancé C,Guillé M,Pinquet J.Time-varying credibility for frequency risk models:estimation and tests for autogressive specification on the random effects[J].Insurance:Mathematics and Economics,2003,33(2):273-282.
[4]Purcaru O,Denuit M.On the dependence induced by frequency credibility models[J].Belgian Acturial Bulletin,2002,2(1):73-79.
[5]Frees E W,Wang Ping.Credibility using copulas[J].North American Acturial Journal,2005,9(2):31-48.
[6]Zellner A.Bayesian and non-Bayesian estimation using balanced loss functions[M].New York:Springer-Verlag,1994:377-390.
[7]Wen Limin,Wu Xianyi,Zhou Xian.The credibility premiums for models with dependence induced by common effects[J].Insurance:Mathematics and Economics,2009,44(1):19-25.
[8]Wu Xianyi,Huang Weizhong.The credibility premiums with common effects obtained under balanced loss functions[J].Chinese Journal of Applied Probability and Statistics,2012,28(2):203-216.
[9]Wen Limin,Wang Wei,Yu Xueli.Credibility models with error uniform dependence[J].Journal of East China Normal University:Natural Science,2009,5:118-126.
[10]Gómez-Deniz E.A generalization of the credibility theory obtained by using the weighted balanced loss function[J].Insurance:Mathematics and Economics,2008,42:850-854.
