光腔中薄膜振子与电磁场耦合关系的数值解

邓志姣 银 燕

（国防科学技术大学理学院物理系，湖南 长沙 410073）

如何将机械振子的运动冷却到量子区域已经成为当前一个重要的研究课题［1］.机械振子的冷却不仅有助于研究和验证宏观尺度下量子力学的一些基本问题，而且还能促进机械振子在量子信息技术和精密测量技术中的应用.目前，利用辐射压力将电磁场和机械振子运动耦合起来的光机械系统［2］为机械振子的冷却提供了一种有利的操作手段.最典型的光机械系统模型为一个F-P光腔，其一端镜面固定，另一端镜面作为机械振子可以自由运动.但这种传统光机械系统不能同时提高振子和光腔的品质因子，因而抑制了冷却的效果.

为克服该局限性，美国耶鲁大学研究小组提出了一种新的薄膜嵌入式光机械系统［3］.其基本结构为：在高品质因子的F-P光腔中，与腔镜面平行放置一个或若干个厚度约为50nm且具有一定透射率的SiN薄膜振子.通过从腔外输入一束或若干束激光驱动与薄膜振子耦合的腔内电磁场模式，就能够达到操控薄膜振子的运动甚至冷却其运动到量子区域的目的.操控薄膜振子运动的系统哈密顿量与薄膜振子和电磁场的耦合关系紧密相关.而该耦合关系又与各个薄膜振子在腔中的位置有关，并且随着振子数的增加变得异常复杂.因此，利用解析的方法求解该耦合关系非常困难.对于单个薄膜振子与电磁场的耦合关系，已有文献给出了数值计算结果［4］，而对于多个薄膜振子的情况其求解还不够全面［5］.本文的目的是以腔内有两个薄膜振子的情况为例，介绍求解光腔中薄膜振子与电磁场耦合关系的基本原理和数值方法.根据该方法可以得到薄膜振子在腔内任意位置处与电磁场的耦合关系，从而方便研究人员选择合适的薄膜振子的位置对振子进行更加有效的冷却.

1 求解薄膜振子与电磁场耦合关系的基本原理

如图1所示，在一个两端镜面固定且全反的F-P光腔中，分别在q1和q2处放置两块相同的电解质薄膜振子.它们的质量均为m、振动频率均为ωm、反射率均为R.由于薄膜振子的引入，光腔会形成新的电磁场本征模式以及相应的本征频率.

图1 F-P光腔中有两个薄膜振子的薄膜嵌入式光机械系统示意图

外加激光操控薄膜振子运动的原理为：外加激光驱动腔内的电磁场模式，腔内的光子对振子产生辐射压力会改变振子的运动；反过来，振子的运动会改变腔内电磁场模式的本征频率以及辐射压力的大小.通过这种作用机制，腔的电磁场自由度与薄膜振子的运动自由度相互耦合起来.由后面即将给出的哈密顿量的形式可知，要得到薄膜振子和电磁场的耦合关系关键是要求出放置薄膜之后腔模的本征频率.假设薄膜振子的厚度远远小于光波的波长，可以设腔内的介电常数为［5］

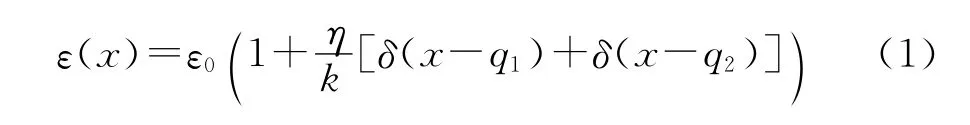
其中，ε0为真空介电常数光波的波数.由于腔的两个镜面全反，腔内电场在x＝±3L处等于零，因此可以设腔内的电场为

利用电场E（x）在q1和q2处的连续性条件，可得

综合式（3）、（4），并消去E1、E2、E3、E4，可以得到波数k满足的方程

当振子的振动频率比邻近腔模频率间隔小很多时，振子的运动不会导致光子在不同的腔模之间相互转换.因此可以只考察腔中的某个电磁场本征模式，其哈密顿量为分别为该本征模式的产生算子和湮灭算子；q、Q算子化后分别为①这种哈密顿量的形式是当振子的振动频率远小于邻近两个腔模频率差时的一个近似的表达式.它可以从严格的哈密顿量取绝热近似得到［6］..假如两个薄膜振子在各自的平衡位置附近做微小振动，可将该哈密顿量在振子运动的平衡位置处进行泰勒展开，

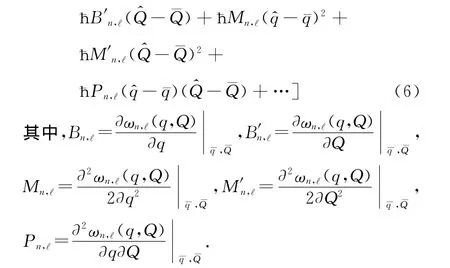
Bn，ℓ（Mn，ℓ）、B′n，ℓ（M′n，ℓ）分别表示该电磁场本征模式与相对运动模式以及质心运动模式的线性（平方）耦合强度，而Pn，ℓ代表了两种集体振动模式和该电磁场模式三者之间的耦合强度.这些耦合强度都是腔模的本征频率在振子的平衡位置处对q、Q及其组合的各阶偏导数.求出它们的大小就求得了薄膜振子与电磁场的耦合关系.将这些耦合系数代入式（6）就能进一步写出操控薄膜振子运动的系统的哈密顿量②整个系统的完整哈密顿量等于式（6）加上薄膜振子的相对运动和质心运动的自由哈密顿量［5］..

2 耦合关系的数值求解及结果分析

由以上分析可以看出，求耦合关系的核心在于求放置薄膜之后腔模的本征频率，即求解方程（5）.方程（5）中含有三角函数，因此它的解有无穷多个并且具有一定的周期性.通过调试并选定k的取值范围求得某个周期内的本征频率值ω1、ω2…ωv（假设一个周期有v个解）.当q、Q在一个不大的区间内变化时，对应相同的k的取值范围存在与格点（qi，Qj）一一对应的v个本征频率值.对于每一组（qi，Qj），可以通过二分法或者牛顿迭代法求本征频率ωℓ（qi，Qj）（ℓ＝1，2，…，v）.以q、Q为二维坐标轴，则ωℓ就能按从小到大的顺序组成v个本征频率曲面.假设R＝0.7，L＝0.1m，k∈

原点，按照上述方法利用Matlab编程运算可以得到三个本征频率曲面，其等高线图如图2所示.

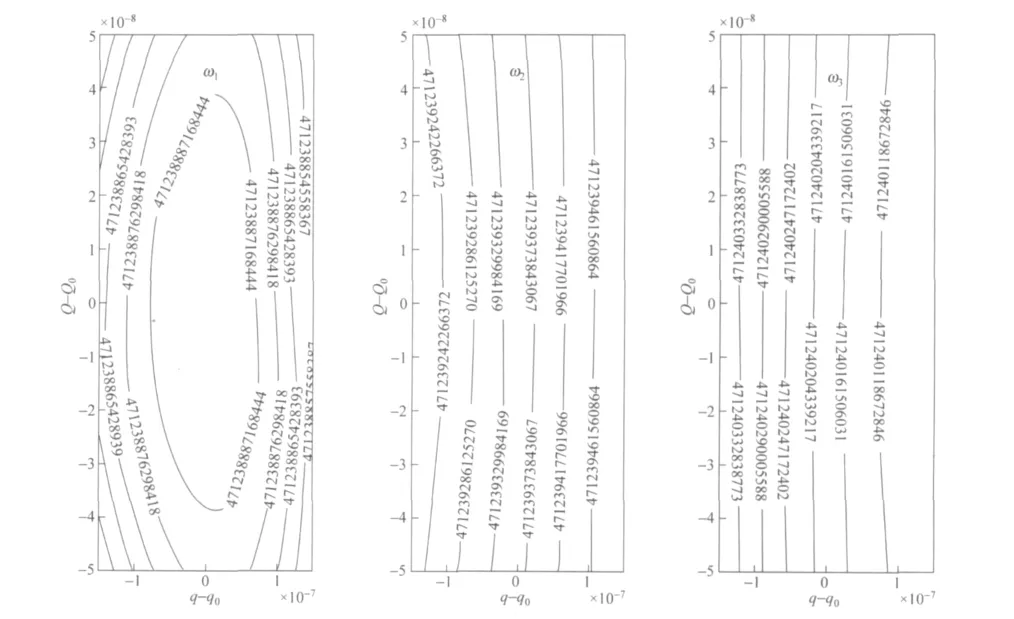
图2 对应q∈［q0-1.5×10-7，q0＋1.5×10-7］m，Q∈［Q0-0.5×10-7，Q0＋0.5×10-7］m范围内三个本征频率曲面的等高线图

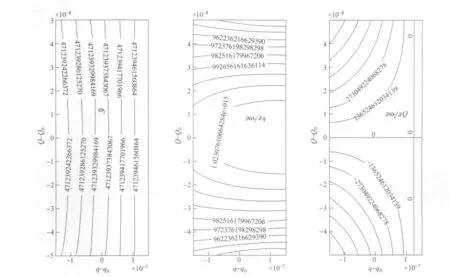
图3 对应q∈［q0-1.5×10-7，q0＋1.5×10-7］m，Q∈［Q0-0.5×10-7，Q0＋0.5×10-7］m范围内第二个本征频率ω2 及其一阶偏导数∂ω2／∂q、∂ω2／∂Q 的等高线图

利用已经得到的每一组（qi，Qj）所对应的本征频率值ωℓ（qi，Qj）（ℓ＝1，2，3），以及求偏导数的差分公式［7］可以进一步求出耦合强度Bℓ（q，Q）、B′ℓ（q，Q）、Mℓ（q，Q）、M′ℓ（q，Q）、Pℓ（q，Q）.图3以本征频率ω2为例，给出了耦合强度B2、B′2的等高线图.若选取＝（q0，0），由数值计算可知该点处B2＝1.03×1015Hz·m-1，B′2＝0Hz·m-1，M2＝2.31×1019Hz·m-2，M′2＝5.59×1021Hz·m-2，P2＝-2.57×1016Hz·m-2.假设m＝4×10-11kg，ωm＝2π×105Hz，温度T＝300K③加上激光驱动腔模之后，光机械耦合的强度会被放大.此外，再通过一些辅助手段（比如增大振子的有效振动频率），我们也可能实现在高温下对薄膜振子运动的有效冷却［8］.，可以＝-6.80×10-6Hz.因此仅保留电磁场与相对运动模式的线性耦合项.哈密顿量式（6）变为

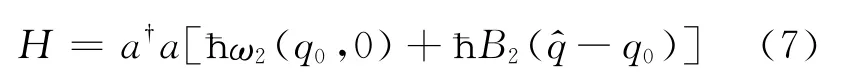
该哈密顿量表明当薄膜振子处于平衡位置（q0，0）并考察腔的ω2本征频率时，主要存在该电磁场模式与两个薄膜振子相对运动模式的线性耦合.

通过改变薄膜振子运动的平衡位置，我们还可以得到其他的光机械耦合形式.例如选取＝（q0-1.2×10-7，3×10-7）m，该平衡位置点附近ω2、∂ω2／∂q、∂ω2／∂Q的取值分布如图4所示.由数值计算可知该点处B2＝3.03×1012Hz·m-1，B′2＝1.29×1015Hz·m-1，M2＝-2.20×1021Hz·m-2，M′2＝-1.35×1021Hz·m-2，P2＝-4.64×1021Hz·m-2.由各耦合项所产生的频移大小为-1.23Hz.因此，当平衡位置为（q0-1.2×10-7，3×10-7）m时，ω2所对应的本征模式主要存在与质心运动模式的线性耦合.哈密顿量式（6）变为

由式（7）、（8）可知，我们可以通过外加激光驱动ω2所对应的腔模，在平衡位置（q0，0）以及（q0-1.2×10-7，3×10-7）m处分别对振子的相对运动模式以及质心运动模式进行操控.所以通过选择薄膜振子合适的平衡位置，就能构造所需的薄膜振子与电磁场的耦合形式，从而有针对性地对振子的振动模式进行加热或冷却.而薄膜振子的平衡位置在实验上是通过一些机械装置进行调节的.

图4 对应q∈［q0-3×10-7，q0］m，Q∈［Q0＋2.5×10-7，Q0＋3.5×10-7］m范围内第二个本征频率ω2 及其一阶偏导数∂ω2／∂q、∂ω2／∂Q 的等高线图

3 总结

本文以光腔中有两个薄膜振子的情况为例，介绍了计算薄膜振子与电磁场耦合关系的基本原理和数值方法.求解过程主要分为两步：第一步建立模型得到放置薄膜之后腔模的本征频率所满足的方程；第二步具体数值求解该方程并计算各项耦合系数.利用该方法可以计算任意多个薄膜振子在腔内任意位置处与电磁场的耦合关系.这些计算为实验工作者选择合适的薄膜振子位置对振子进行更加有效的冷却提供了理论基础.

［1］Schwab K C，Roukes M L.Putting mechanics into quantum mechanics［J］.Phys.Today，2005，7：36.

［2］Marquardt F，Girvin S M.Optomechanics［J］.Physics，2009，2：40.

［3］Thompson J D，Zwickl B M，Jayich A M，et al.Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane［J］.Nature，2008，452：72.

［4］Bhattacharya M，Uys H，Meystre P.Optomechanical trapping and cooling of partially reflective mirrors［J］.Phys.Rev.A，2008，77：033819.

［5］Bhattacharya M，Meystre P.Multiple membrane cavity optomechanics［J］.Phys.Rev.A，2008，78：041801（R）.

［6］Cheung H K，Law C K.Nonadiabatic optomechanical Hamiltonian of a moving dielectric membrane in a cavity ［J］.Phys.Rev.A，2011，84：023812.

［7］数学手册编写组，数学手册［M］.北京：高等教育出版社，2005.

［8］Deng Z J，Li Y，Gao M，et al.Performance of a cooling method by quadratic coupling at high temperatures ［J］.Phys.Rev.A，2012，85：025804.