非奇异弱链对角占优矩阵的逆矩阵无穷大范数的上界

蒋建新

（文山学院 数理系，云南 文山 663000）

非奇异弱链对角占优矩阵的逆矩阵无穷大范数的上界

蒋建新

（文山学院 数理系，云南 文山 663000）

文章研究了非奇异弱链对角占优矩阵A的逆矩阵A-1无穷大范数上界的估计问题，利用弱链对角占优矩阵的逆矩阵元素的上界估计式给出了上界的新的估计式，这些估计式改进了现有的结果。

弱链对角占优矩阵；M矩阵；范数；上界

1 预备知识

Cn×n（Rn×n）表示n×n复（实）矩阵的集合，N={1，2，…，n}，A=（aij）∈Rn×n且aii≠0。

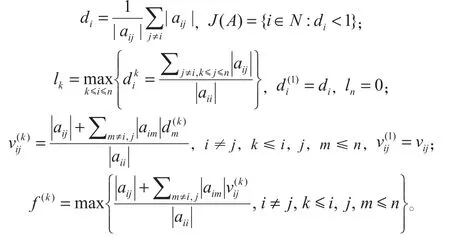
定义1［1］设A=（aij）∈Rn×n，若J（A）=N，则称A为严格对角占优矩阵（SDD）；若A不可约，di≤1，且，则称A为不可约对角占优矩阵（IDD）；若di≤1，，且对i∈J（A），必存在非零元素链，其中i1=i≠i2，…，ir≠ik，0≤r≤k-1，ik∈J（A），则称A为弱链对角占优矩阵（WCDD）。

定义2［1］设A=（aij）∈Rn×n，若aij≤0，A非奇异且A-1≥0（A-1是非负矩阵），则称A是非奇异M矩阵。

定义3［1］设A=（aij）∈Rn×n是非奇异H矩阵当且仅当A的比较矩阵＜A＞是M矩阵，其中

设A=（aij）∈Rn×n，A（n1，n）表示去掉A的前n1行与前n1列得到的A的主子矩阵。

不知有多少年了，这是天葬师第一次在一个风和日丽的上午，离开天葬院，来到天葬场以外的其他地方。青辰推着轮椅，唐玉烟跟在身旁，三个人慢慢地走。轮椅的木轮吱扭吱扭地响，像单调的安眠曲，让人心宁气静。

引理1［3］若A=（aij）∈Rn×n是WCDD的M矩阵，则B=A（2，n）∈R（n-1）×（n-1）也是WCDD的M矩阵，且B-1=（βij）存在，βij≥0，（i，j=2，3，…，n）。

引理2［4］若A=（aij）∈Rn×n是WCDD的M矩阵，B=A（2，n）∈R（n-1）×（n-1），A-1=（αij），B-1=（βij）。则

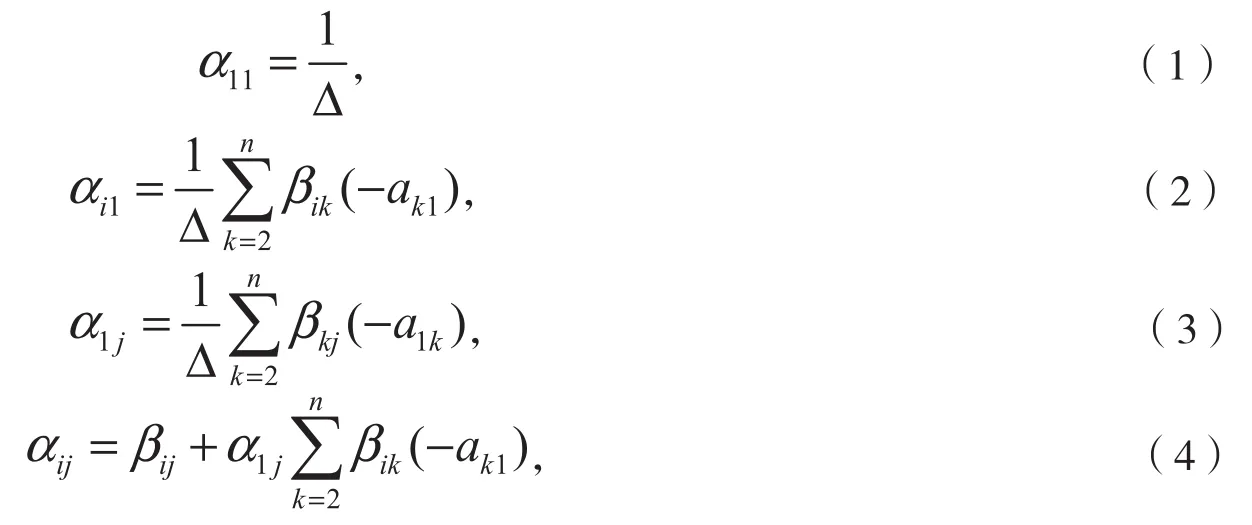
其中，

若J（A）=N，则。

引理3［5］设A，B∈Cn×n，若＜A＞是非奇异M矩阵，则。

引理4［5］设A=（aij）∈Rn×n是SDD，IDD，或WCDD矩阵，则A-1=（αij）满足

且对任意的i∈N有

定理1设A=（aij）∈Rn×n是SDD，IDD，或WCDD矩阵，则A-1=（αij）存在且下列式子成立

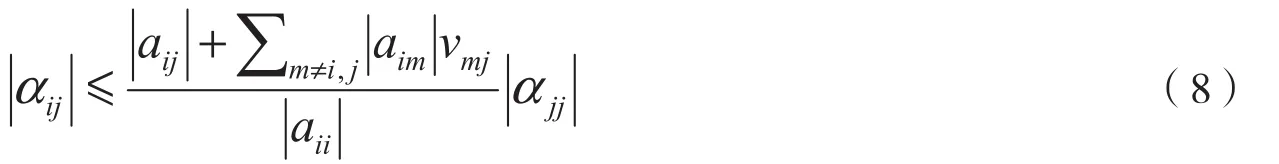
且对任意的i∈N有

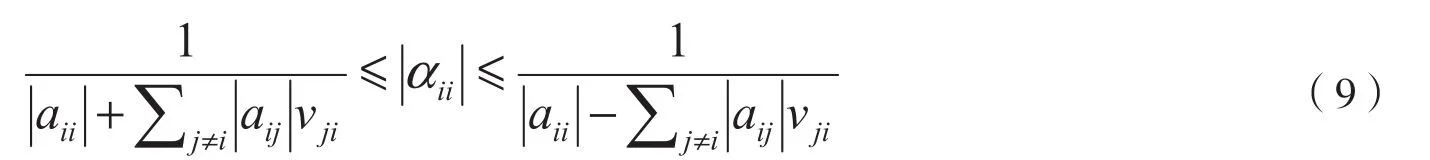
证明：我们仅证明（8）式对于WCDD矩阵成立，其他情况（SDD，IDD）的证明类似。

因为αij是A-1的元素，所以

两边取绝对值应用（6）式得

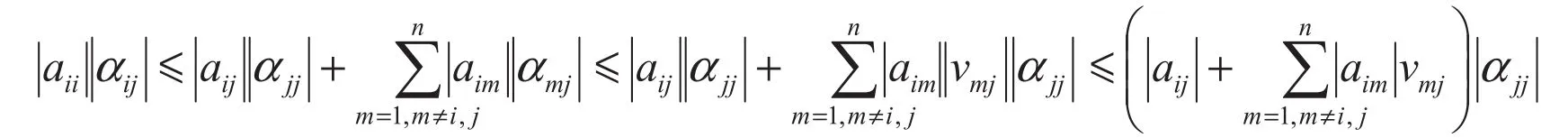
则（8）式得证。

由AA-1=I，有

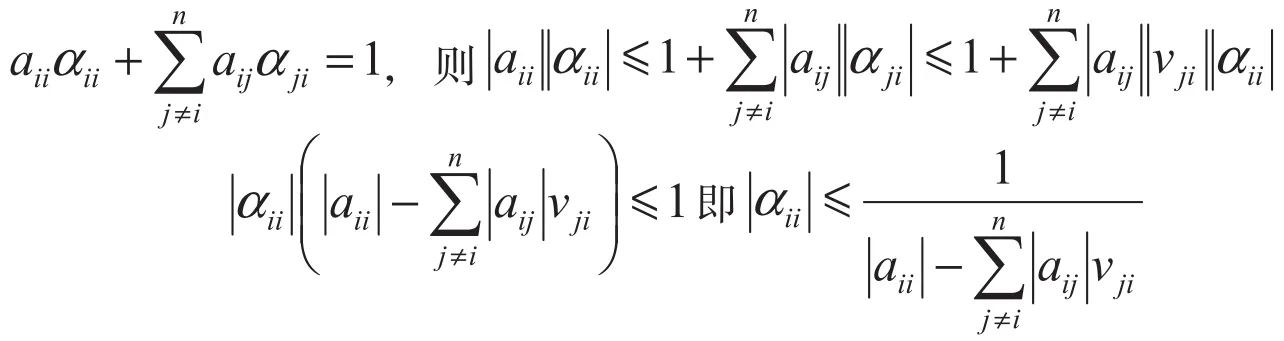
（9）式左边的证明类似于右边的证明。

由di与vij的定义，di≤1，知vij≤di，因此定理1提高了引理4。

定理2设A=（aij）∈Rn×n是WCDD矩阵，B=A（1，n），A-1=（αij），B-1=（βij），则

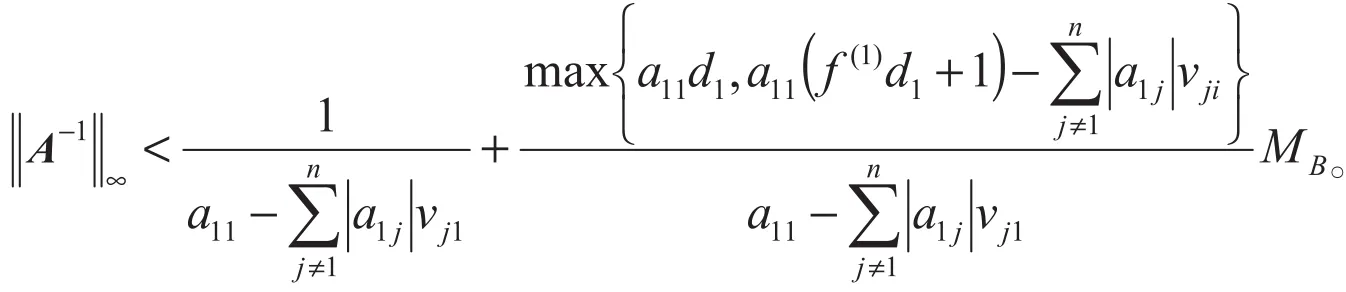
证明：由［3］中的定理3.3 知，A是H矩阵，则＜A＞是非奇异的WCDD的M矩阵。应用引理3得。

所以我们假设AAA是非奇异的WCDD的M矩阵。

由引理2和（9）式

当2≤i≤n时，由（4）式和（8）式得αi1≤f（1）α11

MA=max{h1，hi|2≤i≤n}

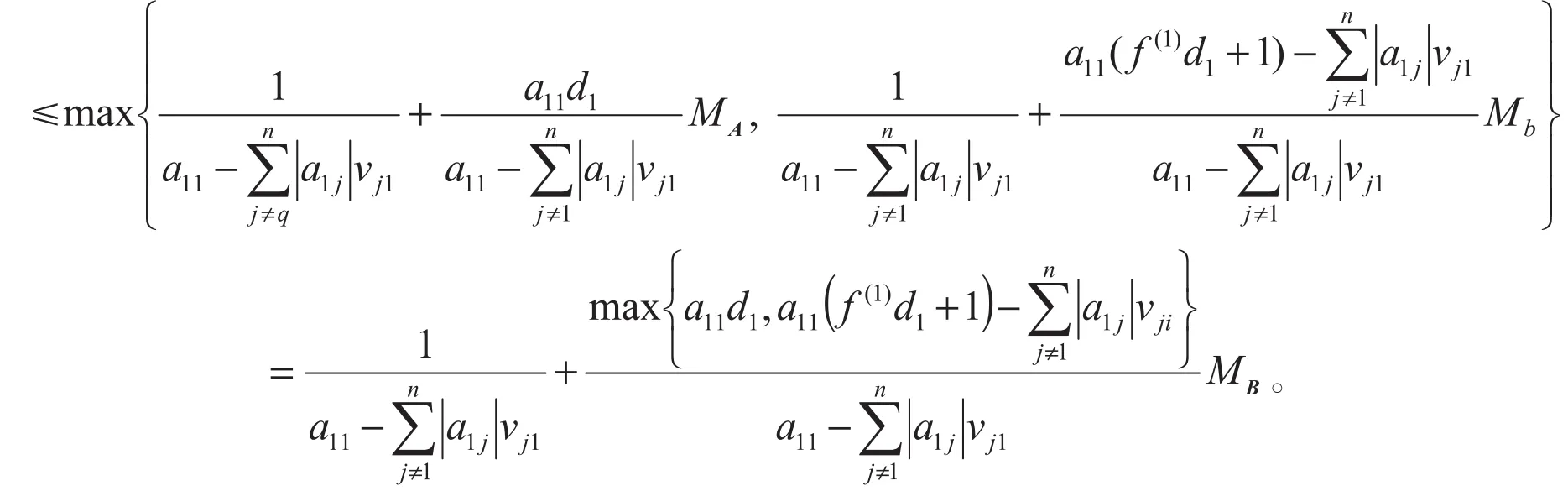
定理3设A是WCDD矩阵，则

证明对定理2应用迭代法即可得证。

数值算例设，容易证明A是WCDD的M矩阵。

［1］陈景良，陈向晖. 特殊矩阵［M］. 北京：清华大学出版社，2000 ：239-276.

［2］黄廷祝，杨传胜. 特殊矩阵分析及应用［M］. 北京：科学出版社，2007：89-95.

［3］Shivakumar P.N.，Chew K.H. A sufficient condition for nonvanishing of determinants ［J］. Proc Amer.Math.Soc, 1974, 43：63-66.

［4］Cheng G-H，Huang T-Z. An upper bound forof strictly diagonally dominant M-matrices［J］. Linear Algebra Appl， 2007，426： 667-673.

［5］Yao-tang Li，Yan-yan Li. Some new bounds on eigenvalues of the Hadamard product and the Fan product of matrices［J］.Linear Algebra Appl，2010， 432： 536-545.

［6］T.Z.Huang， Y.Zhu. Estimation offor weakly chained diagonally dominant M matrices. Linear Algebra and its Applications 2010， 432：670-677.

［7］李艳艳，李耀堂. 严格对角占优M矩阵的逆矩阵的无穷大范数上界的估计［J］. 云南民族大学学报：自然科学版，2012（1）52-56.

［8］蒋建新. 严格对角占优M矩阵的上界的新估计式［J］. 文山学院学报， 2012（3）：36-39.

The Infinity Norm Upper Bound for the Inverse of Nonsingular Weakly Chained Dominant Matrices

JIANG jian-xin
( Department of Mathematics and Physics, Wenshan University, Yunnan 663000 )

The paper studies the problem of estimating upper bounds on the infinite normof the inverse matrix A-1of nonsingular weak chain diagonally dominant matrix A, using the upper bound of elements of inverse matrix of weak chain diagonally dominant matrix gives the new estimation of upper bound of, and improves the existing results.

Weakly chained diagonally dominant matrix; M matrix ; Norm; Upper bound.

O151.21

A

1674-9200（2013）03-0024-04

（责任编辑 刘常福）

2012 - 12 - 20

文山学院重点学科数学建设项目（12WSXK01）。

蒋建新（1981 -），男，甘肃天水人，文山学院数理系讲师，硕士，主要从事微分方程理论及其应用研究。