Modulational instability of the coupled waves between fast magnetosonic wave and slow Alfvén wave in the laser－plasma interaction

Fangping WANG (王芳平), Juanfang HAN (韩娟芳) and Wenshan DUAN (段文山)

College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, People’s Republic of China

Abstract By performing modulational instability analysis of the the nonlinear coupled dimensionless equations between a fast magnetosonic wave(FMSW)propagating obliquely with the magnetic field and a low-frequency slow Alfvén wave (SAW), we obtain the dispersion relation of the perturbation wave.The growth rate of the perturbation wave is obtained.It is found that the growth rate increases as background magnetic field increases, which is in agreement with that reported by Tiwary et al(2016 Phys.Plasmas 23 122307).A critical perturbation wave number is found.When the perturbation wave number is greater than or equal to the critical value, the growth rate is positive and it increases as the perturbation wave number increases, while the wave is stable.The maximum growth rate is reached when the frequency of the FMSW is half of the ion cyclotron frequency.The minimum growth rate is reached when the propagation direction of the perturbation wave is the same as that of the FMSW.

Keywords: modulational instability, magnetic field amplification, laser-plasma interaction

1.Introduction

In recent years, research on controlled thermonuclear fusion has attracted a great deal of attention in order to solve future energy problems.One important topic is the nonlinear interaction between intense laser and plasma.Many studies have shown that modulation instability is inevitable in the interaction process.Therefore, it is important to study the modulation instability in the nonlinear interaction between laser and plasma.

Another extremely important characteristic of intense laser-plasma interaction is the generation of multi mega Gauss strength (～100 MG) magnetic fields, where the intensity of the laser pulses may be greater than 1020W cm-2.It has been reported that when laser pulses with high intensity irradiate a solid target, giant magnetic fields and turbulence can be generated due to laser-plasma interaction [1-4].It is becoming a new regime in plasma physics.The self-generated magnetic field and various instabilities caused by the interaction between an ultra intense pulsed laser and a solid plasma thin target have greatly restricted the research fields of‘fast fire’ in inertial confinement fusion (ICF) and new laserdriven particle accelerators.In many astrophysical phenomena, such as in the case of supernova remnant Cassiopea A,the amplification of magnetic field is observed due to turbulence in plasmas[5-7].The mechanisms of these phenomena in both laboratory and astrophysical plasmas have been studied [8-13].These phenomena are largely related to the fluctuation of plasma.Furthermore, laser-plasma interaction experiments can be possibly used to investigate astrophysical phenomena in the laboratory [14-21] because of the development of high-power laser technology.

The onset of magnetic field and its growth in laboratory and astrophysical plasmas is related to various instabilities,such as modulation instability [22,23],Weibel-filamentation instabilities [24, 25], acoustic and lower hybrid drift instabilities [26], and laser-produced shock [18].

The interaction between an intense laser and plasma can produce various parametric instability processes and nonlinear effects.When the intense laser propagates in plasma,it will cause a kind of long-wave instability,namely modulation instability.Since the growth rate of modulation instability is proportional to the square of the finite amplitude of the incident pump wave,modulation instability is more important than other instabilities.Modulation instability is the result of both the nonlinear effect and the dispersion effect,which will lead to the rupture of a laser wave packet in time or space,and eventually lead to self-focusing.Therefore, it is very important to study the modulation instability and its development for laser propagation in plasma.

When an incident laser beam propagates through plasma,Singh and Sharma[27]found that the laser beam decays into an upper-hybrid wave and a magnetosonic wave at terahertz frequency.There are many studies on the different kinds of waves existing in laser-plasma and interstellar space such as the magnetosonic wave [27-29], Alfvén waves [30], the upper-hybrid wave (UHW) [27, 31] and ion acoustic waves[28, 29, 32-34].It has also been justified [35] that Alfvén waves are generated by fast magnetosonic waves.The evolution of a magnetic field due to the nonlinear coupling between an FMSW propagating obliquely with the magnetic field and a low-frequency slow Alfvén wave(SAW)has been studied [36].There is modulational interaction between magnetosonic waves and driven Alfvén waves.It leads to a nonlinear shift in the plasma frequency in such a way that the amplitude of the magnetosonic pump wave becomes modulated and modulation instability occurs.

The nonlinear coupled equations of a finite-frequency FMSW and an SAW in the presence of the ponderomotive force of the FMSW have also been given [36].Numerical simulation showed that the FMSW may be responsible for the magnetic turbulence during the laser-plasma interaction.It seems that the formation and growth of localized structures depend on the background magnetic field [36].

We are interested in the phenomenon of amplification of magnetic field in laser-plasma interactions and astrophysical plasmas.In this paper,we use the coupling equation between the FMSW and the SAW to study this problem by means of modulation instability analysis.It is found that there is modulational instability.It indicates that the growth rate depends on the background magnetic field, the frequency of the FMSW, as well as the perturbation wave vector.This instability may be the reason for the amplification of the magnetic filed during the interaction between the plasma and the laser.Such an instability is quite important for understanding turbulence in astrophysical phenomena.

This paper is organized as follows: in section 2, the nonlinear coupled dimensionless equations of the FMSW and the SAW are presented, section 3 presents the process of modulation instability analysis and its results,section 4 shows the growth rate of the coupled waves between the FMSW and the SAW, and section 5 consists of the summary and conclusion.

2.Model

The finite-frequency FMSW is considered to be propagating in thexozplane, i.e.k0= (k0x, 0,k0z), with background magnetic field B0= (0, 0,B0).The electric field is taken as E = (Ex,Ey,Ez).The dynamical equation of finite-frequency ω0(ω0≪ ωci, ωciis ion cyclotron frequency) magnetosonic wave can be obtained using basic equations.The plasma is assumed to be collisionless so the thermo-diffusive transport and nonlocal electron transport have been neglected.For momentum, the continuity equation and the Ampere-Maxwell's equation electrons are considered to be inertia-less.Using the two-fluid model with a finite conductivity (which takes care of the magnetic diffusivity), the finite-frequency FMSW equation can be written in terms ofEz[36].

We consider the wave solution ofwhereis the slowly varying function of space and time as compared to the exponential part of the equation.

It is found from the Ampere-Maxwell and Faraday laws thatwhere =vAis Alfvén velocity,andare the slowly varying functions of space and time.Using the two-fluid model with a finite conductivity, the finite-frequency FMSW equation can be written in terms of

The SAW with low frequency ω(ω ≪ ωci)has the wave vector k = (kx, 0,kz).By using the momentum and continuity equation and neglecting the thermal terms,we have the equation of motion of the SAW [36].

Then the nonlinear coupled dimensionless equations(FMSW and SAW) are obtained as follows [36]:

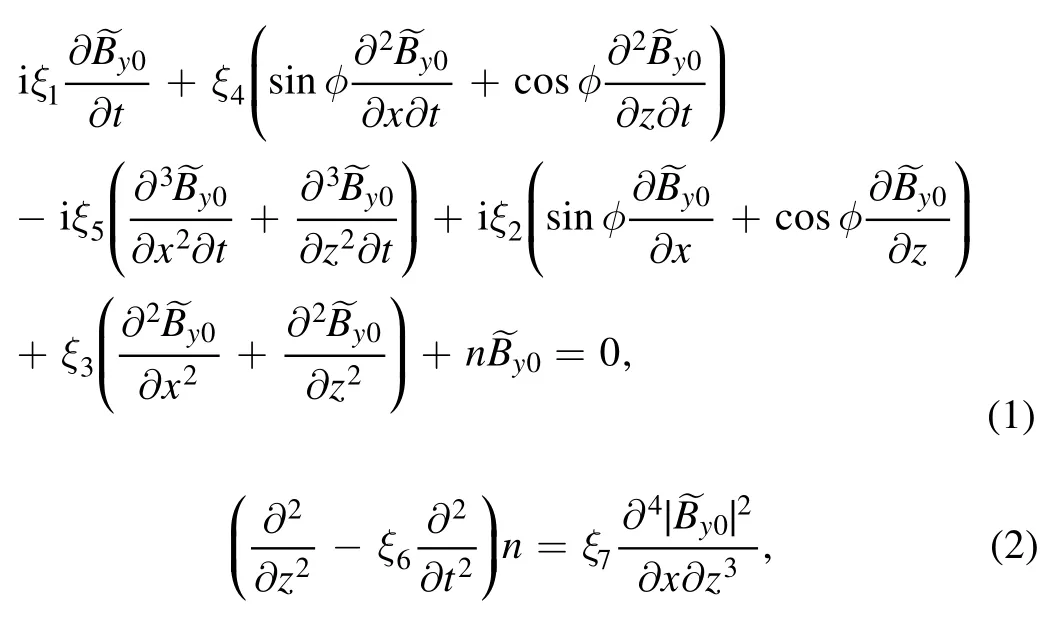
3.Modulational instability

As is well known,modulational instability is one of the most ubiquitous types of instabilities in nature [37].Modulational instability is a characteristic feature of a wide class of nonlinear dispersive systems, associated with the dynamical growth and evolution of periodic perturbations on a continuous-wave background.A long-wave modulation signal(pump wave) is superimposed on a short-wave signal (perturbation wave).The nonlinear distortion occurs in the perturbation wave,that is,the modulation interaction occurs,and with the evolution of time, localized structures, such as independent envelope solitons, will be formed.

In our paper, we find a continuous background wave solution,We assume that a short-wave signal(perturbation wave) is superimposed on the background wave.How does the perturbation wave evolve with time?Is it stable?By substituting the superposition solution into the equation describing the pump wave,we can obtain the dispersion relation of the perturbation wave.We assume that the perturbation wave iswhere the frequency of the perturbation wave is a complex numberThat is to sayIf ImΩ is larger than zero, the amplitude of the perturbation wave increases exponentially with the evolution of time.We call ImΩ the growth rate of instability.We can quantitatively analyze the dependence of ImΩ on system parameters, according to the dispersion relation of the disturbance wave.The following is a detailed process.

We now focus on equations (1) and (2) to perform a standard linear instability analysis of the continuous-wave background.We look for a solution with constant amplitude of the form:then we obtainis the unperturbed plasma number density.represents a continuous-wave solution with a phase or frequency which depends on the square of the amplitude.Is this solution stable under small perturbations?

In order to study the modulational instability of the continuous background waveunder small perturbations, we let both the amplitude and the phase of the continuous background wave be the functions of the quantities ofx,zandtas follows:

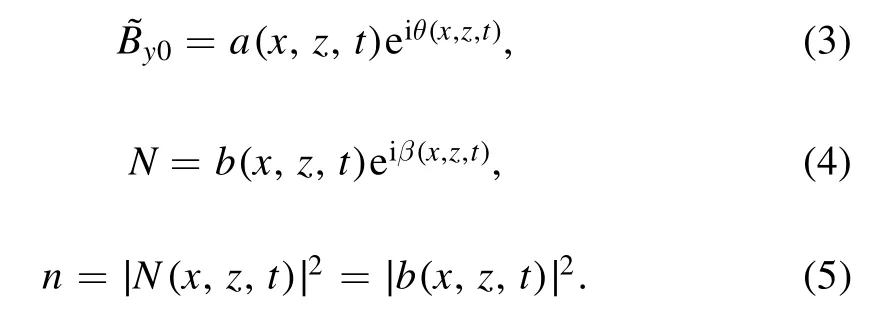
Substituting equations(3)-(5)into equation(1),we obtain the following equations from both the real and the imaginary terms:

We have from equation (2):

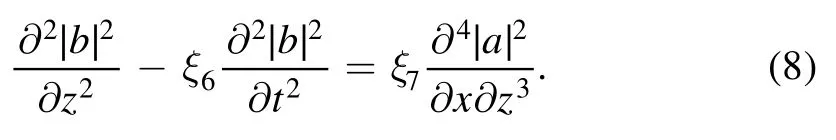
We then consider small perturbations ∈a1, ∈θ1and ∈b1ofa0, θ0andb0, such that:

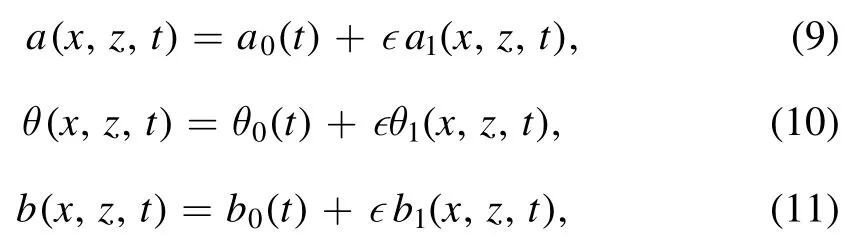
where ε is a small parameter related to perturbation.Substituting equations(9)-(11)into equations(6)-(8),we have at the order of ∈:

We now assume that the perturbations have the form of sinusoidal modulations with wave vector K = (Kx,0,Kz)and frequency Ω:

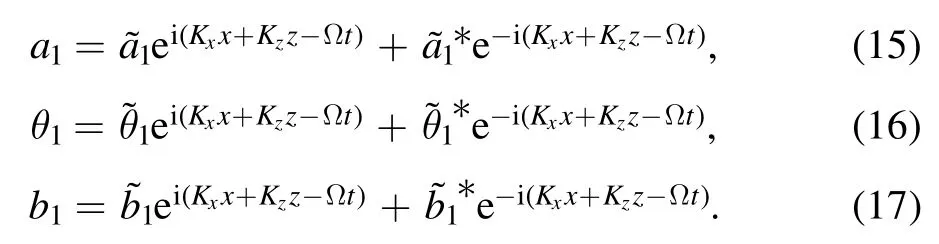
Substituting equations(15)-(17)into equations(12)-(14)and letting χ = i(Kxx+Kzz- Ωt), we have:

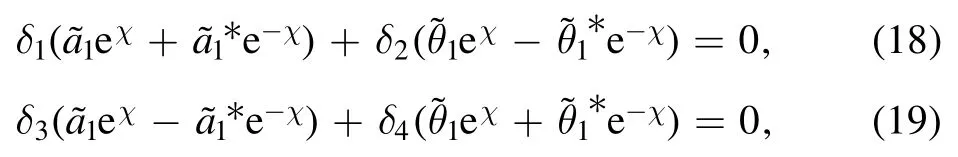
where

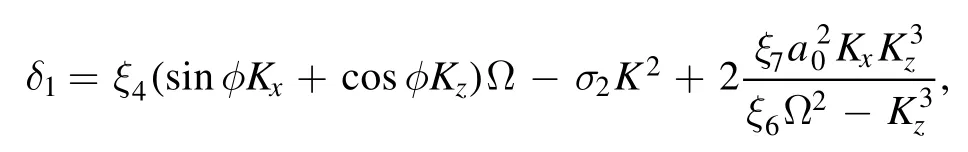
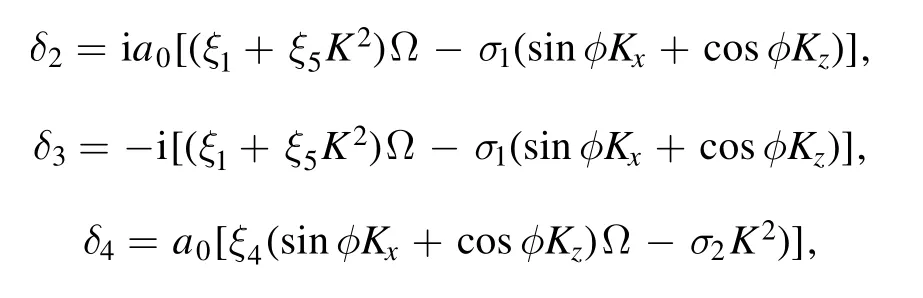
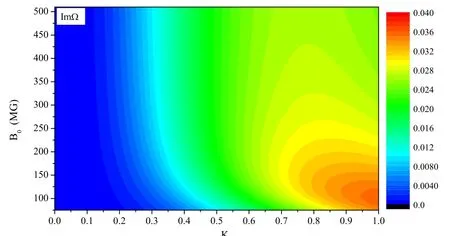
Figure 1.Diagram of the growth rate as a function of background magnetic field B0 and perturbation wave number K with φ = 45°,ω0 = 0.1ωci and θ = 85°.

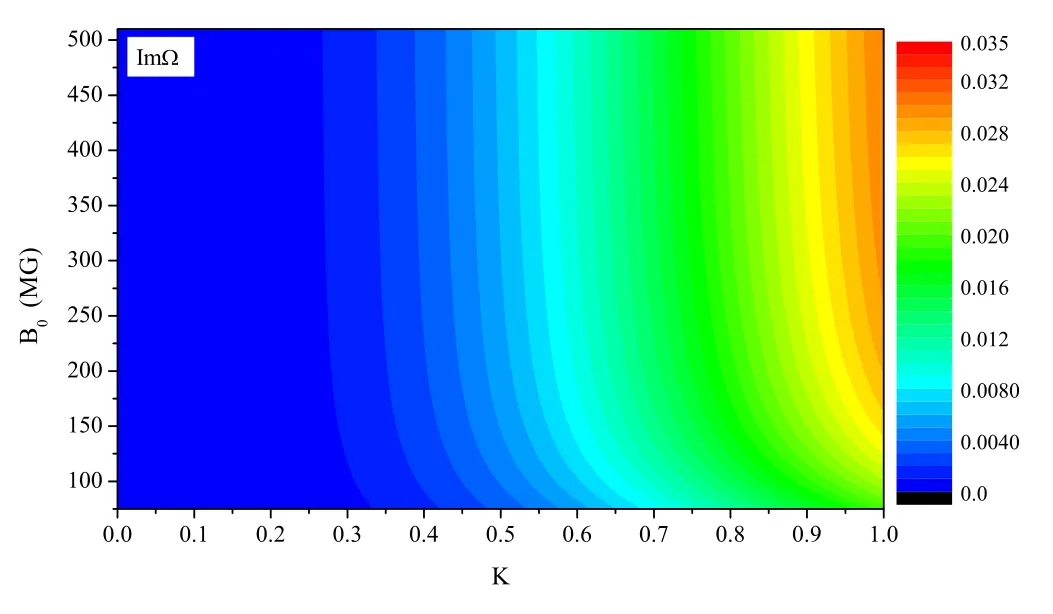
Figure 2.Diagram of the growth rate as a function of background magnetic field B0 and perturbation wave number K with φ = 60°,ω0 = 0.1ωci and θ = 85°.

In order to obtain the nontrivial solution from equations (18) and (19), the coefficient determinant of equations (18) and (19) is equal to zero.The following equation should be satisfied:

We then obtain the following nonlinear dispersion relation:

The perturbation frequency Ω has two parts: the actual wave frequency of the perturbation wave ReΩ and the growth rate of the perturbation wave ImΩ.In other words, if ImΩ ＞ 0, the perturbation wave may be unstable.Otherwise, it is stable.In order to understand the wave instability, we need to solve the solution of ImΩ ＞ 0.

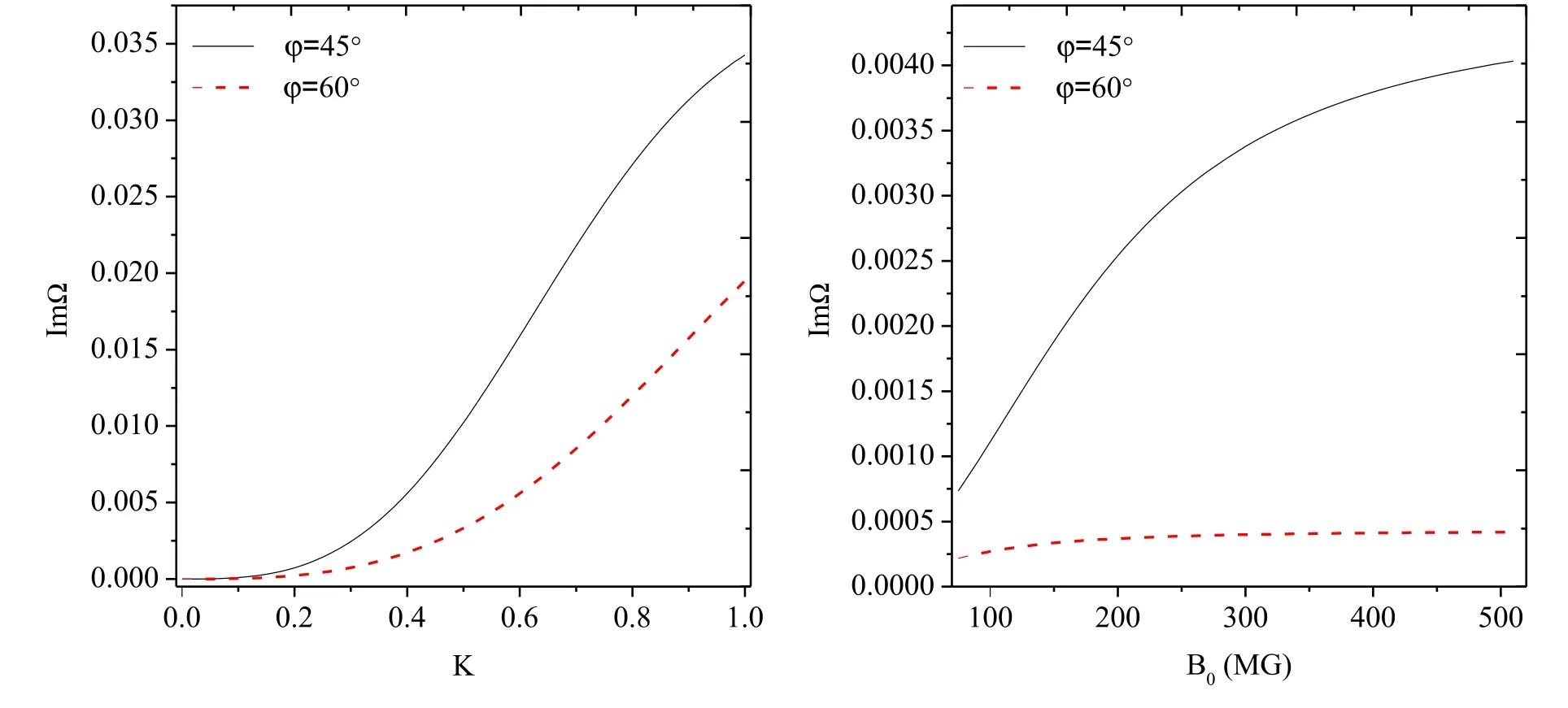
Figure 3.(a) Dependence of the growth rate on the perturbation wave number for different angles between the propagation direction of perturbation wave and the vector the magnetic field(φ),φ = 45°(black line)and φ = 60°(red line),where B0 = 75 MG.(b)Dependence of the growth rate on the background magnetic field B0, where K = 0.2.

4.Growth rate of the coupled waves between the FMSW and the SAW

Notice that not only the coupled wave frequency and the growth rate, but also the instability region can be obtained from equation(21).In the following,we study the growth rate from equation (21) by using the plasma parameters [36]:B0～ 75-500 MG,n0= 2.83 × 1021cm-3,Te= 40 keV andTi= 0.1 keV.The wave parameters are taken as 0.1ωci≤ ω0＜ ωci, ω = 0.001ωci.

Figures 1 and 2 show the imaginary part of Ω for two different cases (φ = 45° and φ = 60°) as a function of the perturbation wave numberKand the background magnetic fieldB0.Both the growth rate ImΩ and wave numberKin figure 1 are dimensionless,i.e.,Ω is in the unit ω0andKis in the unitGrowth rate is presented in colour scale, see in figure 1,where the blue regions correspond to the stability region, while the other regions correspond to the instability region.It is noted from figures 1 and 2 that whenKapproaches zero, the growth rate of instability tends to zero.

In order to appreciate more details about the dependence of the growth rate on the perturbation wave vector K and background magnetic fieldB0, we show two slices of figures 1 and 2 forB0= 75 MG andK= 0.2 in figures 3(a)and (b).

It is noted from figure 3(b) that the growth rate first increases sharply, then increases smoothly as background magnetic field increases.This results are in agreement with those reported in[36],where the magnetic fields areB0= 75 MG,andB0= 100 MG.As magnetic field becomes stronger,localization begins early.

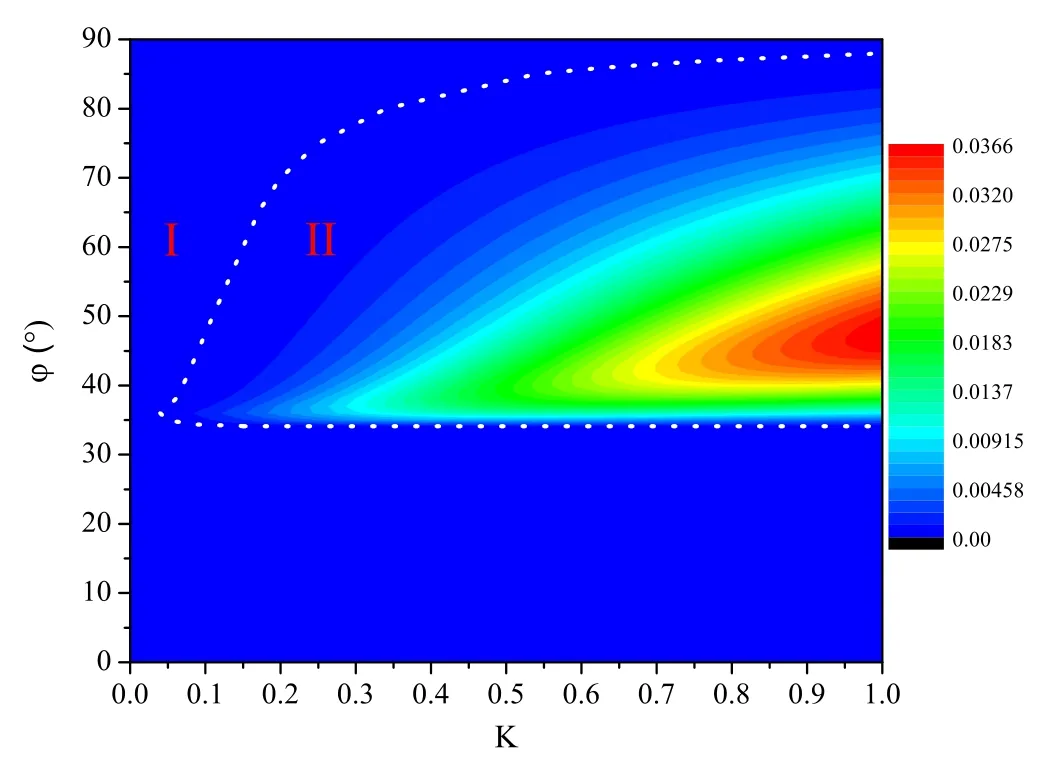
Figure 4.Instability diagram as a function of angle φ and perturbation wave number K with B0 = 100 MG, ω0 = 0.1ωci and φ = 85°.

It can be seen from figure 3(a) that whenK＜Kc, the wave is stable,whereKcis a threshold value.However,whenK≥Kc, the growth rate is positive and it increases asKincreases.Notice thatKcis dependent on angle φ.Figure 4 shows the dependence of the growth rate of perturbation wave ImΩ on both φ, the angle between the perturbation wave vector and the magnetic field, and the perturbation wave numberK.Notice that there are two regions.One is the stable region designated by(I),while the other is the unstable region designated by(II).The thresholdKccorresponds to the white dotted line in the figure 4.

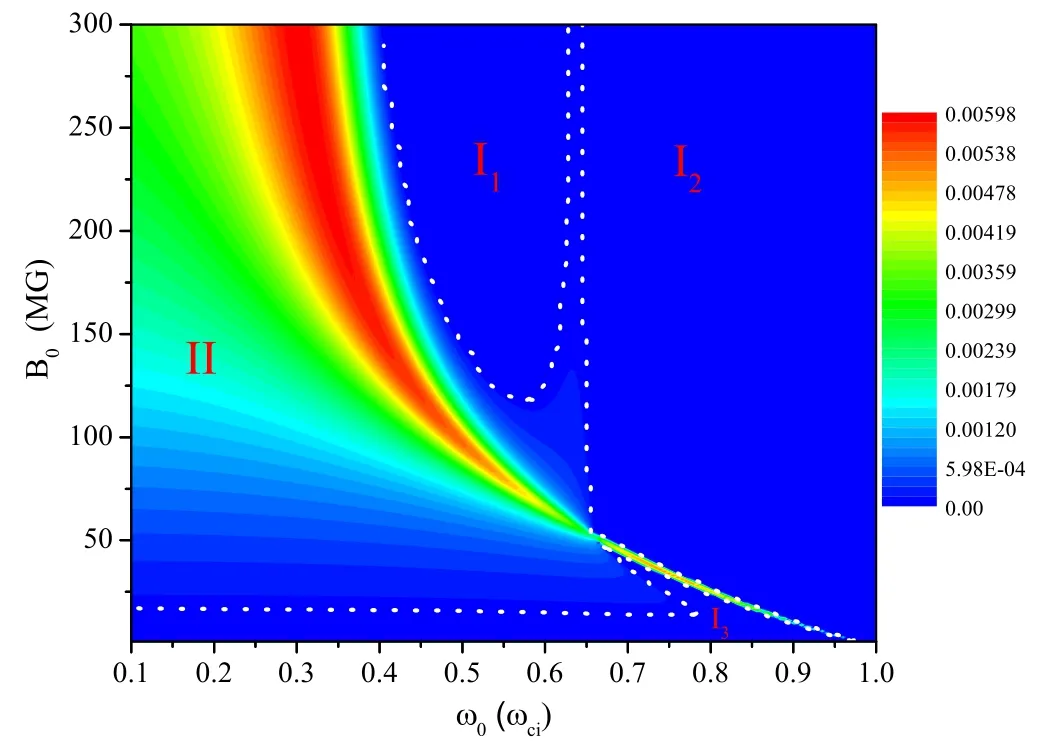
Figure 5.Instability diagram as a function of background magnetic field B0 and frequency of the FMSW ω0 with K = 0.2, φ = 45°and φ = 85°.

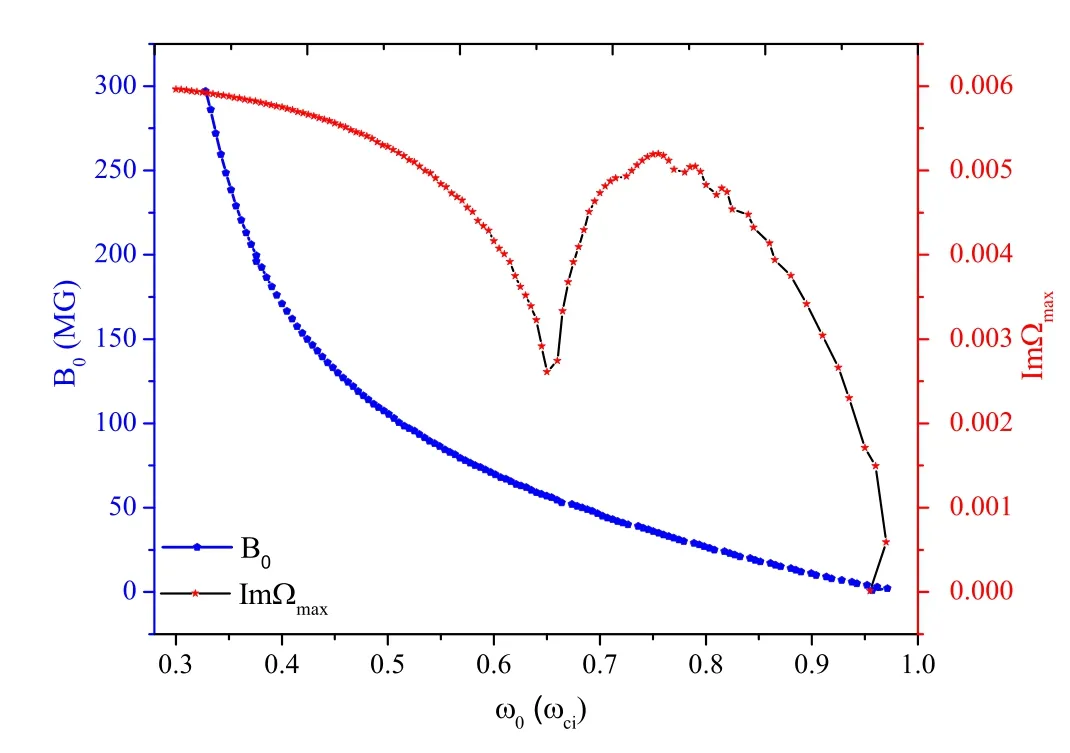
Figure 6.The maximum point of the stable region (blue) and the corresponding maximum growth rate (red) in figure 5.

Now we try to understand how the frequency ω0affects the growth rate of the modulation instability.Figure 5 shows the dependence of the growth rate of perturbation wave on both the frequency of the FMSW ω0and the background magnetic fieldB0.The white dotted lines represent the boundaries of the stable and unstable regions.Notice that there are four regions.Three of them are stable regions(I1, I2, I3), while the other is the unstable region (II).It is observed that there are maximum growth rates which also depend on both ω0orB0.We define the maximum growth rate as ImΩmax.Figure 6 shows the maximum point of the stable region (blue) and the corresponding maximum growth rate ImΩmax(red).It is noted that (ω0/ωci) decreases from 1 to about 0.1 asB0increases.

Figure 7 shows the dependence of the growth rate ImΩ on both the frequency of FMSW ω0and the perturbation wave numberK.Notice that there are two stable regions(I1,I2)and two unstable regions (II1, II2).The boundaries of these regions are plotted by the white dotted lines.We define the maximum growth rates in unstable regions II1and II2as ImΩmax1and ImΩmax2, respectively.Figure 8(a) shows the maximum point of the stable region II1(blue) and the corresponding maximum growth rate(red).Figure 8(b)shows the maximum point of the stable region II2(blue) and the corresponding maximum growth rate (red).It is noted that(ω0/ωci) decreases asKincreases.

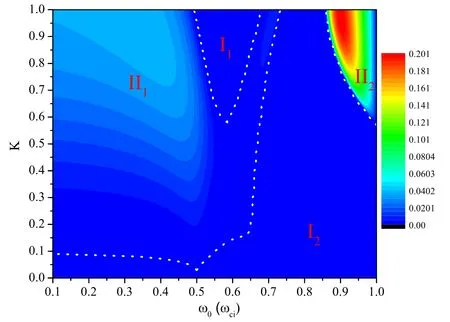
Figure 7.Instability diagram as a function of perturbation wave number K and frequency of the FMSW ω0 with B0 = 100 MG,φ = 45° and φ = 85°.

Figure 9 shows the dependence of the growth rate on frequency of the FMSW ω0and angle φ, the angle between perturbation the wave vector and the background magnetic field.Notice that there are two stable regions (I1, I2)and one unstable region (II).The boundaries of these regions are plotted by the white dotted lines.

Figure 10 shows the dependence of growth rate on φ,the angle between FMSW propagation direction and background magnetic field, and φ, the angle between the perturbation wave vector and the background magnetic field.Notice that there are two stable regions (I1, I2) and one unstable region(II).The boundaries of these regions are plotted by the white dotted lines.In the unstable region,we find that the minimum growth rate is reached on the line of φ = φ.It indicates that the minimum growth rate is reached when the propagation direction of the perturbation wave is same as that of the FMSW.

5.Summary and conclusion

We investigated the phenomena of the magnetic field amplification in laser-plasma interactions by using the nonlinear coupled dimensionless equations (FMSW and SAW)given by Tiwaryet al[36].By performing modulational instability analysis on the the nonlinear coupled dimensionless equations, we obtained the dispersion relation of the perturbation wave.The growth rate of the perturbation wave is obtained.It seems that the amplification of the magnetic field is due to the modulational instability.The larger the growth rate, the stronger the amplification of the magnetic field.Therefore, dependence of the growth rate on system parameters such as the background magnetic field, the frequency and the wave vector of the FMSW, and the wave vector of the perturbation wave have been studied in the present paper.

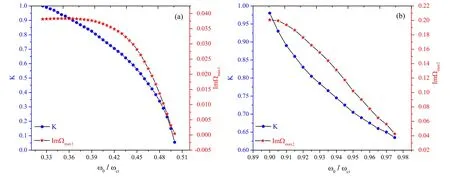
Figure 8.(a)The maximum point of the stable region II1(blue)and the corresponding maximum growth rate ImΩmax1(red)in figure 7;(b)the maximum point of the stable region II2 (blue) and the corresponding maximum growth rate ImΩmax2 (red).

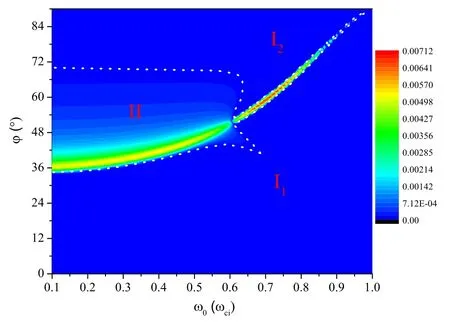
Figure 9.Instability diagram as a function of angle φ and frequency of the FMSW ω0 with B0 = 100 MG, K = 0.2 and φ = 85°.

Figure 10.Instability diagram as a function of angle φ and angle φ with B0 = 150 MG, ω0 = 0.1ωci and φ = 85°.

A threshold of perturbation wave numberKcis found.WhenK≥Kc, the growth rate is positive whileK＜Kcthe growth rate is zero and the wave is stable.Kcis related to other parameters of the system, such as φ.

Moreover, the dependence of the growth rate on the character of the FMSW is given.The angle between the propagation direction of FMSW and the background magnetic field has an obvious effect on the growth rate.The minimum growth rate is reached when the propagation direction of the perturbation wave is the same as that of the FMSW, i.e., θ = φ.

The background magnetic field also has a great effect on the growth rate.It is found that the growth rate increases as background magnetic field increases, which is in agreement with that reported in [36].

Acknowledgments

This work was supported by National Natural Science Foundation of China (No.11 965 019).