普通高校体育课教学与课外体育活动关系的现状分析

梁冠琦，刘艳明

Physical Education Deprtment，Huazhong Normal University，Wuhan Hubei，430079

教育部《关于2010年全国学生体质与健康调研结果的公告》显示，我国学生的体质与健康目前令人担忧。

体育课程是学校体育教育的主要渠道和基础。它是以学生身体为主要手段，通过合理的体育教育和科学的体育锻炼过程；达到增强体质、增进健康和提高体育素养目标的公共必修课程；是学校体育课程体系的组成部分；是高等学校体育工作的中心环节。

课外体育锻炼是大学体育课程的重要组成部分，是体育课的补充与拓展，也是实现体育教学目标的重要手段与有效途径。课外体育锻炼是学生在体育课外参加有组织的体育活动。要实现体育课程的运动参与目标，运动技能目标，身体健康目标，心理健康目标及社会适应目标。单纯依靠课堂教学很难实现上述目标。而课外体育锻炼是体育课堂教学的延续和补充，课外体育锻炼主要侧重满足学生身体需要，提高运动能力为主。学生在完成课堂教学的同时，根据个人兴趣，爱好参加各种项目体育俱乐部活动，教师根据各项不同需求进行辅导。

本文正是依托改善和提高我国学生体质健康水平的大背景，讨论体育课教学与课外体育活动之间的关系，目的在于通过对体育课教学和课外体育活动研究，不仅切实改善我国学生各类专项身体素质水平，还为提高普通高校体育课质量提供理论参考。

1 研究对象与方法

1.1 研究对象

随机选取湖南长沙五所普通高校200名本科生作为研究对象。

1.2 研究方法

1.2.1 文献资料法

通过在华中师范大学图书馆、中国期刊网等资源查阅了近年来国内外发表的有关体育课教学和课外体育活动关系的期刊论文、专著，收集和整理了大量数据材料和文字资料。

1.2.2 个案访谈法

对长沙某大学的部分体育老师和同学，采取个案访谈调查，主要目的是根据其反馈意见，对初步设计的问卷进行修改和完善。

1.2.3 问卷调查法

问卷内容主要包括对学生体育课选修情况、课外体育活动情况、以及部分相关个人信息的调查。问卷发放主要利用长沙某大学学生上课前或上课后的集中时间，最终发放学生问卷234份，回收有效问卷222份，有效回收率为95%。

1.2.4 回归分析法

在本文的研究中，回归分析法主要被用来确认因果。确认因果通常是在两个变量有理论上联系的前提下，通过多元回归分析控制初期变量，确认剩下的两个变量在统计上是否有实证意义的联系。

2 结果与分析

2.1 问卷描述统计

在回收的总共222份问卷中，所有人都回答了上次选修体育课所取得的成绩。在这222人中间，没有人回答不及格。其中90分以上的占15%，80分－89分的占32.5%，70分－79分的占29.5%，60－69分的占23%（见图1）。

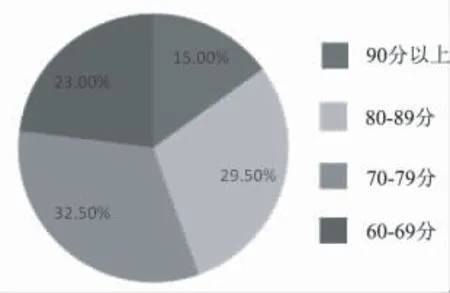
图1 学生上次选修体育课时总评成绩的分布

在回收的总共222份问卷中，所有人还回答了一周进行课外体育锻炼的时间数。在这222人中间，每周锻炼2 h以上的占15%，锻炼1－2 h的占17.5%，锻炼0－1 h的占35%，几乎不锻炼的占32.5%（见图2）。

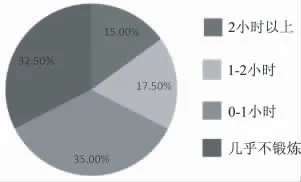
图2 学生每周锻炼时间的分布

值得一提的是，尽管我们仅仅调查了长沙五所普通高校的200位大学生，但并不代表我们最终的结论只适用于这200名大学生。我们的思路是从总体中抽出一小部分进行观察和研究，然后推断出总体的性质，这一小部分，也就是长沙五所普通高校的200位大学生，称之为样本。在稍后的回归模型和回归结果部分，我们将对样本进行统计分析。

2.2 回归模型

现在让我们考虑方程1：

其中Score代表体育课分数，Physical＿Trainning代表每周参加的课外体育活动时间，Height代表身高，Weight代表体重，Male代表性别，其中男性＝1，女性＝0，Science代表文理科，其中文科＝0，理科＝1。在这个模型里，我们假设一个学生的体育课成绩取决于他的身高、体重、性别、文理科，另外还有我们关注的核心变量——每周参加课外体育活动的时间。身高、体重是容易理解的，一个人的身高、体重通常来说描述了这个人的基本身体条件，身高更高、体重更大（在一定的范围内），通常来说更容易在体育课中取得好的成绩；性别、专业也类似，通常来说男生、理科学生在体育课上的表现更为优秀。当然，我们最关心的还是每周参加课外体育活动的时间。我们试图通过对β1的估计来衡量Physical＿Trainning对Score的影响，即课外体育活动是否对体育课教学有促进作用。

一个易于理解的猜测是，给定其它条件不变，也就是控制住所有的人的身高、体重、性别和文理科，当一个人投入更多的时间在课外体育活动上时，他会在体育课上取得更高的分数。这里面的原因可能有三个——

首先，当一个人投入更多的时间在课外体育活动上时，他会有更多的机会练习体育课上学习的各种项目。例如体育课仅仅教会了一个人三步上篮的基本动作要领，但是要流畅、熟练、准确地完成这个动作，还需要课下不断的练习。

其次，当一个人投入更多的时间在课外体育活动上时，即便他没有练习体育课上学习的那个项目，但由于不同的体育运动之间存在相通之处，也会提高他的体育课成绩。例如一个人在课外体育活动中主要参加足球项目，但经常参加足球项目无疑会提高身体协调性，增强心肺能力，也会对体育课上其它项目成绩的提高带来帮助。

第三，当一个人投入更多的时间在课外体育活动上时，也更容易培养出对体育运动的热爱，这样当他回到体育课上时，也会更加投入，更容易取得好成绩。

因此Physical＿Trainning的系数β1应该是显著正的。因此我们有假说1。

假说1：给定其它条件不变，每周参加更多的课外体育活动会有利于体育课成绩的提高。

另外再考虑硬币的另外一面，体育课教学是否又对课外体育活动产生了积极的影响？我们同样预计这个影响是正面的，因此我们得到假设2。

假说2：给定其它条件不变，体育成绩更好的同学更倾向于参加课外体育活动。

相应的，我们也有方程2：

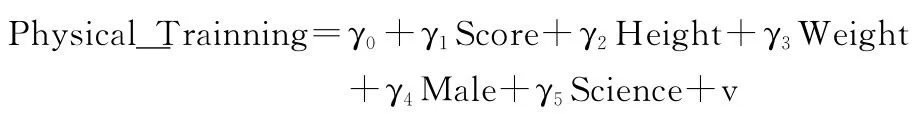
与前面类似，我们也假设一个学生的课外体育活动取决于他的身高、体重、性别、文理科，另外还有我们关注的核心变量——他的体育课成绩。值得一提的是，我们的方程1与方程2是完全对称的，也就是说Physical＿Trainning和Score其实是互相决定的，因此单独对方程1和方程2进行两次估计在统计上是不被接受的。根据古扎拉蒂（2000）的《计量经济学》，以及J.M.伍德里奇（2003）的《计量经济学导论：现代观点》［4－5］，我们需要两个工具变量，在方程1中，工具变量IV1与Physical＿Trainning相关而与Score不相关，同样在方程2中，工具变量IV2与Score相关而与Physical＿Trainning不相关。为了简便起见，假设收入只受上面提到过的那些因素的影响，考虑一个简单的回归方程：

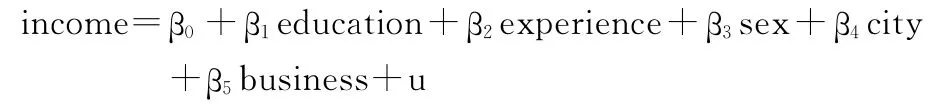
即个人收入是因变量，被受教育程度、工作经验（工作年限）、性别、城市、行业所决定，因此受教育程度等都是自变量。

通过回归分析，我们能够估计出β1、β2、β3、β4、β5，而知道了β1、β2、β3、β4、β5的符号（正负），也就知道了受教育程度、工作经验（工作年限）、性别、城市、行业这5个自变量对收入的影响到底是正还是负；另外β1、β2、β3、β4、β5绝对值的大小，也衡量了这5个自变量对收入影响的具体程度。

另外值得一提的是，由于我们在回归方程中同时放入了5个变量，我们得到的结果就保证了“控制住其它因素的影响”。比方说教育education的系数就意味着假定其它条件不变，即假定工作经验（年限）、性别、城市、行业都相同，一个人多受一年教育，他的收入会增加多少。使用多元回归分析讨论因果，通常是在两个变量有理论上联系的前提下，通过多元回归分析控制住其它影响因素，确认剩下的两个变量在统计上是否有实证意义的联系。在这里，控制住其它影响因素是非常重要的。一个简单的例子是，我们想弄清楚家庭经济状况对子女的身高是不是有影响，因为从理论上说，一个家庭越富裕，越能为子女提供相应的营养条件，因此家庭经济状况越好，子女的身高越高——但是，决定子女身高的因素还有很多，比方说最重要的可能是父母的身高，另外还有这个孩子本身的性别（因为男孩通常来说比女孩更高），因此我们必须运用一种统计方法，控制住其它因素的影响（比方说父母身高、孩子性别），这时候我们就要用到多元回归。又比如，劳动经济学里有一个经典的命题是——教育会使得这个人的收入更高。在这个命题中，收入是被教育程度决定的，而教育程度决定着这个人的收入，因此收入在这里是因变量，教育程度则是自变量。另外决定一个人收入的因素还有很多种，例如这个人的工作经验（工作年限）、这个人的性别、这个人工作的城市、这个人工作的行业等等，因此我们有不止一个自变量，这就是一个典型的多元回归。

我们使用宿舍到体育场的距离作为工具变量IV1，也就是我们假设宿舍到体育场的距离越近，同学们每周花在课外体育活动上的时间就越多，但是宿舍到体育场的距离远近本身并不能决定体育课的考试成绩。类似地，我们使用最近一次选修体育课时逃课的次数作为工具变量IV2，也就是我们假设选修体育课时逃课的次数越少，最后的分数就越高，但是否逃课本身并不能决定同学们每周花在课外体育活动上的时间。因此我们有分别加入工具变量IV1和IV2的两个方程3和方程4：

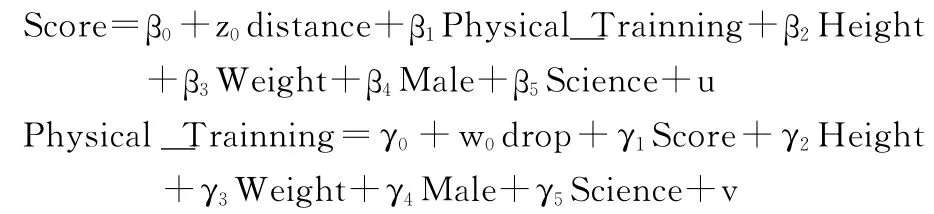
其中distance和drop分别代表宿舍到体育场的距离，和最近一次选修体育课时逃课的次数，接下来两阶段最小二乘法估计对β1和γ1的结果就回答了前面提到的两个问题：课外体育活动是否对体育课教学有促进作用？体育课教学是否又对课外体育活动产生了积极的影响？同时也可以证明假说1以及假说2是否成立。

2.3 回归结果

回归结果如表1和表2所示。第一列代表的是变量名称，第二列代表的是回归系数，第三列代表的是t统计量，第四列代表的是相应的P值。回归结果表的系数代表了自变量对因变量的影响程度。其中回归系数衡量了，给定其它条件不变，当某个自变量变动一个单位（身高增加1 cm、体重增加1 kg、宿舍到体育场的距离增加1 000 m、体育课逃课次数增加1次、从女性到男性、从文科到理科）时，对因变量产生多大的影响，即体育课分数增加多少分，课外体育活动每周多参加几次；t统计量则反映了这个影响在统计上是不是显著的；P值与t统计量相对应，较大的t统计量意味着较小的P值，一般而言，P值至少要小于0.1时才被接受为是显著的，此时称之为在10%的显著性水平上显著，而小于0.05、0.01则称之为在5%、1%的显著性水平上显著。

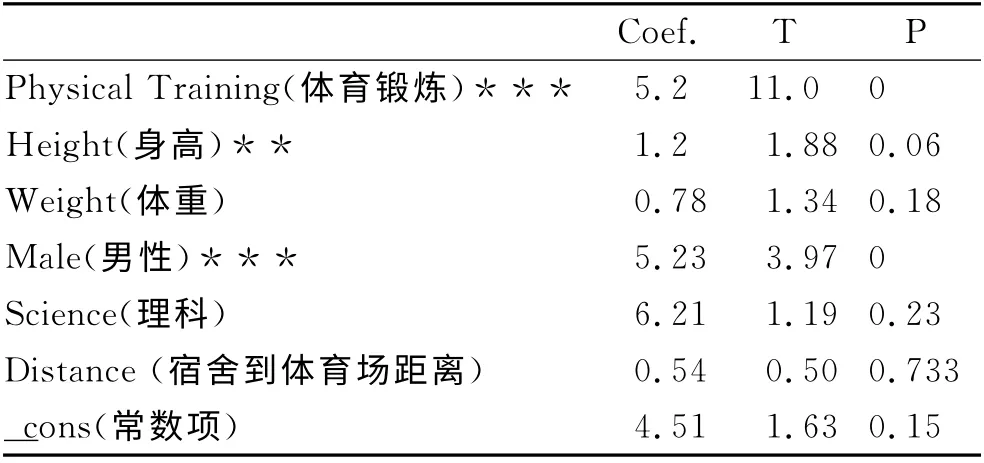
表1 最终的估计结果1

表2 最终的估计结果2

例如考虑表2，Height（身高）的系数是1.2，代表身高每增加1cm，从平均的意义上而言，这个学生的体育课成绩会提高1.2分，并且在5%的显著性水平上显著，即此假设被拒绝的可能性低于5%。

又例如考虑表3，Male（男性）＊＊＊的系数是1.02，代表男性相对于女性，从平均的意义上而言，男生相对于女生每周参加课外体育活动的次数会增加1.02次，并且在1%的显著性水平上显著，即此假设被拒绝的可能性低于1%。

当然，本文讨论的主要内容并不是身高是否会促进学生的体育课成绩，或者男生是否更愿意参加课外体育活动。体育课成绩是受很多因素影响的，其中包括参与课外体育活动的积极程度，同时参与课外体育活动的积极程度也受很多因素影响，其中也包括体育课程成绩。如同回归分析可以告诉我们，控制住其它因素，或者说假定其它条件不变，更好家庭经济条件是不是使得孩子们拥有更高的身高、或者更多的教育是不是使得这个人拥有更高的收入，我们也可以利用回归分析讨论，更高的体育课成绩是不是使得学生参与课外体育活动更加积极，以及学生参与课外体育活动更加积极，会不会使得他们的体育课成绩更高。当然，我们也必须控制住其它因素的影响。之所以将这些变量考虑进来，是我要用多元回归的方法控制住其它变量的影响。

现在回到体育课与课外活动的关系上来。

表2显示，Physical Training（体育锻炼）的系数是5.2，代表每周多参加1次课外体育活动，从平均的意义上而言，这个学生的体育课成绩会提高5.2分，并且在1%的显著性水平上显著，即此假设被拒绝的可能性低于1%。

同时表3也显示，Score（体育课分数）的系数是0.19，代表体育课成绩每提高1分，从平均的意义上而言，这个学生的每周会多参加0.19次课外体育活动，并且在1%的显著性水平上显著，即此假设被拒绝的可能性低于1%。

因此我们的假说1：给定其它条件不变，每周参加更多的课外体育活动会有利于体育课成绩的提高，以及假说2：给定其它条件不变，体育成绩更好的同学更倾向于参加课外体育活动，都得到了问卷调查和回归分析的证实。

3 结论与建议

3.1 结论

1）Physical Training（体育锻炼）的系数是5.2，代表每周多参加1次课外体育活动，从平均的意义上而言，这个学生的体育课成绩会提高5.2分，并且在1%的显著性水平上显著，即此假设被拒绝的可能性低于1%。同时Score（体育课分数）的系数是0.19，代表体育课成绩每提高1分，从平均的意义上而言，这个学生的每周会多参加0.19次课外体育活动，并且在1%的显著性水平上显著，即此假设被拒绝的可能性低于1%。2）因此我们的假说1：给定其它条件不变，每周参加更多的课外体育活动会有利于体育课成绩的提高，以及假说2：给定其它条件不变，体育成绩更好的同学更倾向于参加课外体育活动，都得到了问卷调查和回归分析的证实。也就是说课外体育活动的确对体育课教学有促进作用；体育课教学从分数的角度上也对课外体育活动产生了积极的影响。

3.2 建议

1）各级教育管理部门、学校，要更加重视体育课教学活动的开展。有了规范保证的体育课教学，才会有蓬勃发展的各项课外体育活动。2）各级教育管理部门、学校，也要更加重视课外体育活动的开展。有了蓬勃发展的各项课外体育活动，体育课教学才不会成为无源之水、无本之木。3）各级教育管理部门、学校，也要更加重视针对体育课教学和课外体育活动的理论研究工作。有了相应的理论作为指导，实际工作将会有更大的突破，整个体育事业也会有更大的发展。

［1］ 张 勇.普通高校体育课程课内外一体化的研究［J］.安徽体育科技，2009，12（6）：56－58.

［2］ ［美］古扎拉蒂.计量经济学［M］.北京：中国人民大学出版社，2000.

［3］ ［美］J.M.伍德里奇.计量经济学导论：现代观点［M］.北京：中国人民大学出版社，2003.

［4］ 王丹红.清华大学百年体育之路回眸［J］.科学时报，2008，25（1）：32－35.

［5］ 陈德芳.浅谈课外体育活动的意义［J］.现代教育教研杂志，2007，26（6）：18－21.

［6］ 陈玉萍.浅谈体育课与课外体育活动的关系［J］.中国体育教育，2006，37（5）：32－35.