土石围堰边坡稳定的多因素综合风险分析

罗立哲，胡志根，刘 全，皮凌华

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 湖北省汉江河道管理局，潜江 433100)

土石围堰边坡稳定的多因素综合风险分析

罗立哲1，胡志根1，刘 全1，皮凌华2

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 湖北省汉江河道管理局，潜江 433100)

土石围堰边坡稳定受堰体土石料力学性质、施工洪水及导流建筑物泄流能力等多种不确定性因素影响，为进行更全面、准确的风险估计，综合考虑水文、水力和土石料力学参数的随机性，在分析相关参数的分布形式和统计特征值的基础上，通过Monte-Carlo方法耦合仿真分析堰前水位分布和围堰边坡稳定性，建立土石围堰边坡稳定多因素综合风险计算模型，统计分析度汛期间土石围堰边坡稳定综合风险．实例分析表明，该模型计算的围堰边坡稳定综合风险率小于仅考虑单个随机因素的边坡稳定风险率，更准确地反映了实际工程土石围堰边坡稳定状态．

边坡稳定；多因素风险分析；Monte-Carlo方法；土石围堰

水利水电工程土石围堰导流系统中，边坡失稳是出现最频繁、带来损失最大且最难弥补的破坏形式，围堰边坡失稳风险率常作为工程设计和施工的重要参考指标．以往研究集中讨论土石料力学参数为随机变量情况下的边坡失稳风险，如Cambou等[1]根据线性理论，采用随机有限元方法对土坡进行了可靠度分析；张继周等[2]在试验的基础上获得了主要岩土力学参数的概率分布模型及选择标准；徐卫亚等[3]对岩土材料力学参数的模糊统计特征进行了研究；刘春原等[4]对岩土参数随机场特性和线性预测做了分析和研究；李典庆等[5]将随机响应面法运用于边坡可靠度分析；傅旭东等[6]提出了基于Monte-Carlo法的岩土工程失效概率和可靠度计算指标等．但土石围堰边坡稳定不仅受土石料力学性质不确定性影响，还与施工洪水和导流建筑物泄流能力的随机性密切相关；仅考虑单一随机因素的风险分析方法难以准确描述土石围堰边坡稳定状态，需建立综合多随机因素的风险计算模型分析土石围堰边坡稳定．

笔者分析并确定水文、水力和土石料力学性质等随机因素相关参数的分布类型和统计特征值，通过仿真拟合堰前水位分布曲线，在此基础上建立土石围堰边坡稳定综合风险计算模型，并率定模型的计算参数，评估度汛过程中的土石围堰边坡稳定多因素风险.

1 影响围堰边坡稳定的随机因素分析

土石围堰边坡失稳破坏指洪水超过某一界限时，作用于围堰的荷载大于其抗力，导致围堰边坡稳定失效．其中，荷载滑动力矩主要由堰前水位决定，抗力抗滑力矩主要由堰体材料力学性质决定．

1.1 堰前水位随机性分析

堰前水位分布根据施工洪水工况和导流建筑物泄流工况进行调洪演算得到，根据实测水文资料，按放大典型洪水过程线方法确定计算洪水过程线，最大洪峰流量为P-Ⅲ型随机抽样均值，其密度函数为

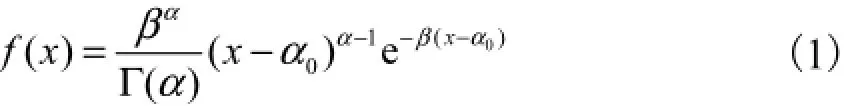
式中：α、β和α0分别为P-Ⅲ型分布的形状、刻度和位置参数；Г(α)为伽马函数．

导流建筑物规模确定时，受围堰上游水位和泄流建筑物水力参数的不确定性影响，导流系统的泄流量具有随机性，一般服从三角形分布，其分布函数为

式中：a′为泄流能力下限；b′为平均泄流能力；c′为泄流能力上限；a′、b′、c′均通过导流建筑物施工及运行的统计资料确定．

1.2 堰体土石料随机性分析

堰体土石料的随机性主要表现在凝聚力c、内摩擦角φ和容重γ等物理力学指标上．其中，c、φ的变异性影响较大，而容重γ的变异性影响很小[7-9]．因此，本文假设容重为定值，仅考虑c和φ的随机性，确定其相关参数的统计特征值和分布类型．

1) 参数统计特征值确定

本文采用随机模糊统计理论分析堰体土石料力学参数的统计特征[10]．获取容量为n的某岩土力学参数实测样本(x1，x2，…，xn)，记随机模糊均值为．取A˜为U={x1，x2，…，xn}上的模糊子集，令μ˜(xi)为元素xi对˜A的隶属度(i=1，2，…，n)．根据

A理论经验，μ˜A(xi)采用指数函数形式[11]，而模糊权重系数ωij的表达式为

式中djmax和djmin分别为的最大值和最小值，i=1，2，…，n．

为明确模糊集合中的元素对其隶属度的标准，取核点作为参照点，对式(4)求一阶导数并令其为0，可得

式中：d1,max、d1,min分别为的最大值和最小值，i=1，2，…，n．

同理，可得样本方差表达式为

式中d2,max、d2,min分别为的最大值和最小值，i=1，2，…，n．

2) 参数分布拟合

土石料力学参数分布的确定常采用拟合检验方法，假设参数服从某一种或几种经典的理论分布，在χ2检验法和K-S检验法基础上，根据经验函数和假设理论分布函数的偏差，定义拟合优度指标，利用该指标对假设分布进行检验，确定参数的最优拟合概率分布[12]．根据实践经验，某一岩土力学参数只可能服从有限的几种分布，如凝聚力c可能服从正态分布或极值Ⅰ分布，内摩擦角函数tan,φ可能服从正态分布或对数正态分布．

正态分布概率密度函数为

极值Ⅰ型分布函数为

式中：a为分布的尺度参数；u为分布的位置参数．

对数正态分布概率密度函数为

式中：α为形状参数，α＞0；μ为比例参数．

2 土石围堰边坡稳定综合风险模型

假设堰前水位与堰体土石料力学参数为相互独立的随机变量，将围堰边坡失稳看作某定水位条件下的随机事件，则堰前水位为h且围堰边坡失稳的风险率为

式中：f(h)为堰前水位分布的概率密度函数；Fr(h，φ，c)为堰前水位为h时围堰边坡失稳的条件概率．

围堰度汛过程中围堰边坡失稳的综合风险率为

式中hmax和hmin分别为度汛期间堰前最高水位和最低水位．将堰前水位分布曲线在[hmin，hmax]区域内划分为N段区间，运用离散化数值积分方法可将式(12)转化为

由式(13)可知，计算土石围堰度汛过程边坡失稳风险率需拟合堰前水位分布曲线、建立定水位条件下围堰边坡失稳风险计算模型，并将两者耦合．假设施工洪水来流量和导流建筑物泄流能力的分布类型，利用Monte-Carlo方法模拟施工洪水过程和导流建筑物泄流过程，通过系统仿真进行调洪演算，统计分析确定围堰上游水位分布，得到堰前水位分布曲线[13].将度汛过程中堰前水位计算区域划分为N段区间，在确定土石料力学参数统计特征值和概率分布类型的基础上，利用Monte-Carlo法计算以区间两端点作为固定堰前水位的围堰边坡失稳条件概率，其中最危险滑动面和边坡安全系数的选择和计算可采用多种方法，本文根据简化Bishop法确定[14]，进而得到各段水位区间内围堰边坡失稳的条件概率均值．土石围堰边坡稳定的综合风险率模型计算流程如图1所示．

图1 土石围堰边坡稳定综合风险率计算流程Fig.1 Calculation flow chart of rock-fill cofferdam slope stability comprehensive risk

定水位条件下围堰边坡失稳风险率计算流程如下：

(1) 输入逻辑关系、围堰几何数据、材料参数统计特征值、分布类型及仿真次数M；

(2) 确定该水位下最危险滑动面；

(3) 产生随机数群，不确定量抽样c、φ；

(4) 不同分布下的变量随机数转换；

(5) 将变量随机数带入功能函数，计算边坡稳定；

(6) 依据判别准则，统计围堰边坡失稳次数n，可得Fr(h，φ，c)=n/M．

3 实例分析

3.1 工程概况

某水电站装机12,600,MW，正常蓄水位600,m，双曲拱坝最大坝高278,m，正常蓄水位以下库容115.7×108,m3．根据文献[15]，选定Ⅲ级导流建筑物，土石类围堰相应设计洪水标准为重现期20～50年．

根据电站坝址下游水文站实测的各施工时段洪水特性(见表1)，综合分析水文系列资料、导流建筑物工程量及施工工期等，拟定初期施工导流标准为50年一遇，洪水流量QP=2.0%=32,000,m3/s；根据调洪演算可得设计水位530,m，围堰高75,m．施工导流建筑物采用两岸对称布置6条导流隧洞，其断面尺寸为18,m×20,m，进口高程368,m，出口高程360,m，导流洞泄流糙率取值范围为0.014～0.017．

围堰堰体填筑材料主要来自现场开挖料，根据工程资料数据的拟合检验分析，凝聚力c服从极值Ⅰ型分布，内摩擦角函数tan φ服从对数正态分布．对3个典型开挖点的土石料抽样并进行单轴饱和抗压强度试验，土石料非随机性和随机性力学参数如表2和表3所示．运用随机模糊理论处理表3中的参数样本，可得堰体土石料力学参数随机变量c、tan,φ相关特征值如表4所示．

表1 设计洪水资料Tab.1 Flood data of design

表2 土石料非随机性力学参数Tab.2 Nonrandom mechanics parameters of earth and rock t/m3

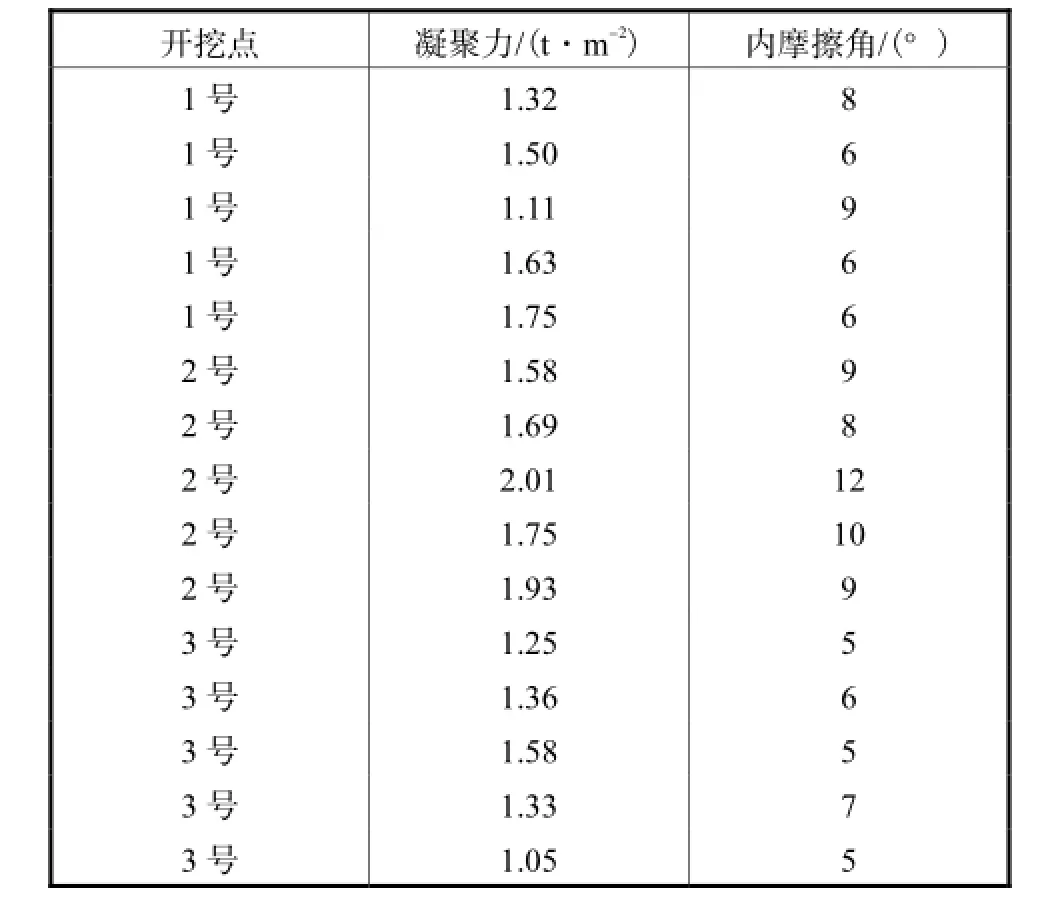
表3 土石料随机性力学参数样本试验结果Tab.3 Random mechanics parameters sample of earth and rock

表4 土石料随机性力学参数特征值Tab.4Random mechanics parameters eigenvalue of earth and rock

3.2 围堰边坡风险率计算

根据水文、水力资料，分别拟合洪水过程线、泄流过程线，仿真得到上游水位分布曲线；以20,m、15,m、10,m、5,m、3,m和1,m为堰前水位计算分区步长，根据土石围堰边坡稳定综合风险模型，计算度汛过程围堰边坡失稳综合风险率R．围堰为Ⅲ级导流建筑物，因此以g(k) =k-1.3＜0作为边坡失稳判定式，其中k为边坡安全系数．表5为计算分区步长为10,m时的围堰边坡失稳风险率计算结果，图2为计算分区步长与围堰边坡失稳风险率关系．

表5 围堰边坡失稳综合风险率计算结果(计算分区步长：10,m)Tab.5 Calculation results of cofferdam slope stability comprehensive risk(step size：10,m)

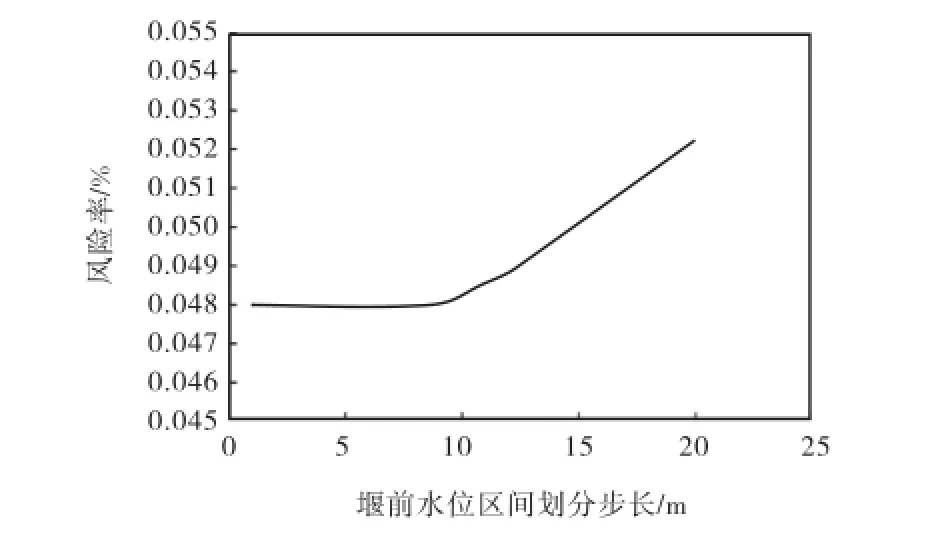
图2 堰前水位分区步长与边坡失稳风险率关系Fig.2 Relationship between step size of water-level upstream and cofferdam slope stability risk

3.3 计算结果分析

由图2可知，堰前水位计算分区步长对风险计算结果有一定程度影响，计算分区步长越小，计算结果越精确；当步长小于10,m时，计算所得风险值趋于稳定，步长影响可忽略不计．

仅考虑土石料力学性质随机性的围堰边坡失稳最大风险率为0.125%；由表5可知，考虑多因素的围堰度汛过程边坡失稳综合风险率为0.048%，远小于仅考虑土石料力学性质随机因素的边坡失稳风险率计算结果；在围堰设计过程中，以边坡稳定多因素综合风险率为参考能更好地界定导流系统风险与投资的关系，避免风险高估导致的工程量和工程成本的浪费．

4 结 论

(1) 本文实例分析表明土石围堰边坡稳定综合风险模型中堰前水位计算分区步长对计算结果有一定程度影响，但当步长小于临界值时，影响忽略不计.

(2) 考虑水文、水力和土石料力学参数随机性的土石围堰度汛过程边坡稳定综合风险率远小于仅考虑单个随机因素的边坡稳定风险率，能够更真实地反映实际工程土石围堰边坡稳定状态．

(3) 全面描述围堰边坡稳定风险还需进一步分析如洪水时程、水位壅高等其他随机因素，风险分析模型尚待在工程实践中不断完善．

［1］ Deluzarche R，Cambou B. Discrete numerical modelling of rockfill dams[J]. International Journal for Numerical and Analytical Methods in Geomechanics，2006，30(11)：1075-1096.

［2］ 张继周，缪林昌. 岩土参数概率分布类型及其选择标准[J]. 岩石力学与工程学报，2009，28(增2)：3526-3532.

Zhang Jizhou，Miao Linchang. Types and selection criteria of probability distribution of rock and soil parameters [J]. Chinese Journal of Rock Mechanics and Engineering，2009，28(Suppl 2)：3526-3532(in Chinese).

［3］ 徐卫亚，蒋中明. 岩土样本力学参数的模糊统计特征研究[J]. 岩土力学，2004，25(3)：342-346.

Xu Weiya，Jiang Zhongming. Research on fuzzy eigenvalues of samples of rock and soil[J]. Rock and Soil Mechanics，2004，25(3)：342-346(in Chinese).

［4］ 刘春原，闫澎旺. 岩土参数随机场特性及线性预测

[J]. 岩土工程学报，2002，24(5)：588-592.

Liu Chunyuan，Yan Shuwang. Characteristic of the random field of geotechnical parameters and linear prediction [J]. Chinese Journal of Geotechnical Engineering，2002，24(5)：588-592(in Chinese).

［5］ 李典庆，周创兵，陈益峰，等. 边坡可靠度分析的随机响应面法及程序实现[J]. 岩石力学与工程学报，2010，29(8)：1513-1523.

Li Dianqing，Zhou Chuangbing，Chen Yifeng，et al. Reliability analysis of slope using stochastic response surface method and code implementation [J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(8)：1513-1523(in Chinese).

［6］ 傅旭东，茜平一，刘祖德. 边坡稳定可靠性的随机有限元分析[J]. 岩土力学，2001(4)：413-418.

Fu Xudong，Qian Pingyi，Liu Zude. The reliability analysis for slope stability by perturbation stochastic finite element method[J]. Rock and Soil Mechanics，2001(4)：413-418(in Chinese).

［7］ Liu Linlin，Li Jianqiao，Fan Shichao，et al. Effects of soil compaction to its shear property [C]//2011 2nd International Conference on Advanced Measurement and Test. Nanchang，China，2011：530-533.

［8］ 孙冬梅，冯 平，张明进. 考虑气相作用的降雨入渗对非饱和土坡稳定性的影响[J]. 天津大学学报，2009，42(9)：777-783.

Sun Dongmei，Feng Ping，Zhang Mingjin. Refined analysis of stability of unsaturated soil slope due to rainfall infiltration considering the effect of gas phase [J]. Journal of Tianjin University，2009，42(9)：777-783(in Chinese).

［9］ Tan Zhuoying，Cai Meifeng. Multi-factor sensitivity analysis of shallow unsaturated clay slope stability [J]. Journal of University of Science and Technology Beijing：Mineral Metallurgy Materials(Eng Ed)，2005，12(3)：193-202.

［10］ 孙立川，张海平，周念清. 随机-模糊统计方法在岩土特征参数指标统计中的应用[J]. 岩土力学，2012，33(3)：821-826.

Sun Lichuan，Zhang Haiping，Zhou Nianqing. Application of random-fuzzy statistical method to statistics of geotechnical parameters [J]. Rock and Soil Mechanics，2012，33(3)：821-826(in Chinese).

［11］ Giasi C I，Masi P，Cherubini C. Probability and fuzzy reliability analysis of a sample slope near Aliano[J]. Engineering Geology，2003，67(1)：391-402.

［12］ 舒继森，郭兵兵，张俊阳，等. 基于拟合优度指标评价的岩土参数概率分布研究[J]. 采矿与安全工程学报， 2008，25(2)：197-201.

Shu Jisen，Guo Bingbing，Zhang Junyang，et al. Research on probability distribution of parameters of rock and soil based on fitting optimization index [J]. Journal of Mining and Safety，2008，25(2)：197-201(in Chinese).

［13］ 范锡峨，胡志根，靳 鹏. 基于Monte-Carlo方法的施工导流系统综合风险分析[J]. 水科学进展，2007，18(4)：604-608.

Fan Xi′e，Hu Zhigen，Jin Peng. Integrated risk of construction diversion system based on the Monte-Carlo method[J]. Advances in Water Science，2007，18(4)：604-608(in Chinese).

［14］ 林跃忠，王铁成，王 来，等. 三峡工程高边坡的稳定性分析[J]. 天津大学学报，2005，38(10)：936-940.

Lin Yuezhong，Wang Tiecheng，Wang Lai，et al. Stability analysis of high excavated slope in three gorges project [J]. Journal of Tianjin University，2005，38(10)：936-940(in Chinese).

［15］ 中华人民共和国水利部. SL303—2004水利水电工程施工组织设计规范[S]. 北京：中国水利水电出版社，2004.

The Ministry of Water Resources of the People’s Republic of China. SL303—2004 Specifications for Construction Planning of Water Resources and Hydropower Engineering[S]. Beijing：China Water and Power Press，2004(in Chinese).

Comprehensive Risk Analysis of Rock-Fill Cofferdam Slope Stability Considering Multiple Random Factors

Luo Lizhe1，Hu Zhigen1，Liu Quan1，Pi Linghua2
(1. State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2. River Authority of Hubei Hanjiang，Qianjiang 433100，China)

The slope stability of rock-fill cofferdam is related to many random factors，such as mechanical properties of cofferdam filling materials，flood of construction period，and flood discharge of diversion structures. In order to estimate the risk of cofferdam slope stability more precisely and roundly，the uncertainty of hydrology，hydraulics and earth-rock mechanics parameters was considered by analyzing their probability distribution forms and statistical characteristics，and then water-level upstream distribution and cofferdam slope stability were simulated synthetically by Monte-Carlo method to establish the comprehensive risk model for rock-fill cofferdam slope stability，which was used to analyze the comprehensive risk of rock-fill cofferdam slope stability during flood season. The case study shows that the comprehensive risk of rock-fill cofferdam slope stability calculated by the model is smaller than the risk with only random factor considered，and the comprehensive risk can more accurately reflect the stability condition of rock-fill cofferdam slope in practical projects.

slope stability；multi-factor risk analysis；Monte-Carlo method；rock-fill cofferdam

TV511.3

A

0493-2137(2013)07-0617-06

DOI 10.11784/tdxb20130708

2012-07-31；

2012-10-26.

国家自然科学基金资助项目(10902078，51079115)．

罗立哲（1987— ），男，博士研究生，wwtony@whu.edu.cn.

胡志根，zhigenhu@163.com.