跨阻型集成带阻滤波器设计

李 锵，轩秀巍，李 琨，滕建辅,

(1. 天津大学电子信息工程学院，天津 300072；2. 天津理工大学电子信息工程学院，天津 300384)

跨阻型集成带阻滤波器设计

李 锵1，轩秀巍2，李 琨2，滕建辅1,2

(1. 天津大学电子信息工程学院，天津 300072；2. 天津理工大学电子信息工程学院，天津 300384)

作为一种独特的滤波器形式，跨阻滤波器在集成电路中起着重要作用．基于LC原型电路，提出了一种跨阻型集成带阻滤波器的设计方法．首先用状态变量表示LC元件变量关系，然后将关系式表示成信号流图形式，用全差分放大器替换其中的积分部分，最后集成得到全差分有源跨阻带阻滤波器．为验证设计的可行性，给出了六阶Chebyshev跨阻集成带阻滤波器的设计过程及其Hspice计算机仿真结果．仿真结果表明，所设计的滤波器满足设计参数要求，滤波性能良好．

跨阻；带阻滤波器；无源梯形网络；有源滤波器；运算模拟

通信技术和多媒体技术的迅速发展对信号处理提出了越来越高的要求．而滤波器作为信号处理的关键元件，其性能优劣直接影响到整体集成电路的性能．传统的滤波器都是采用电压输入-电压输出的形式，当它和电流形式的元件相连时需要在中间接入电流-电压转换器，增加了电路的元件数量和功耗[1-3].跨阻滤波器作为一种新型滤波器，其输入为电流信号，输出为电压信号，可直接与输出为电流的传感器或D/A转换器等相连，避免了电流-电压的转换，降低了硬件的总体复杂度[4]．跨阻滤波器因其输入阻抗小，低噪声，且可线性提高混频器的电压摆幅，得到了很多研究者的关注[5-7]．文献[5]提出了一种单放大器双二阶节跨阻滤波器结构，得到的跨阻有源RC电路具有良好的噪声和线性特性．

带阻滤波器(亦称带除滤波器或陷波滤波器)是一种除了一个单独的频带之外能通过其他所有频率的滤波器．有源带阻滤波器在消除噪声干扰方面得到广泛应用，但其稳定性和可重复性有待提高．带阻电路的设计比较单一，大多都采用高通电路和低通电路相串联的方法．这样的设计不仅复杂度高，所得到的带阻滤波器的敏感度和功耗等性能都不十分理想．而传统的集成有源滤波器设计往往以传递函数为出发点，分别用双二次节和一阶环节实现，然后再对其进行级联得到[8]．众所周知，级联设计法具有设计简单、调试方便等优点，但其缺点是响应对元件变化敏感度高．反馈设计具有级联结构的模块式特点，又能提供比级联结构优越的敏感度特性，但这种电路结构比较复杂，调节困难，使其应用受到一定限制．双端接载的无源LC梯形网络具有响应对元件变化敏感度低的特点，且电路结构简单，调试方便，适用于设计对组件精度和稳定性要求苛刻的有源滤波器[9-12]．文献[11]提出了基于LC梯形原型的对数域滤波器设计方法，相对于文献[12]，2种设计方法均简单易行，得到的电路都具有电流线性特性，但文献[11]有效减少了所需元件的个数．

笔者提出了基于LC滤波网络的跨阻型带阻滤波器的设计方法．首先用数学方程表示LC元件变量关系，然后将关系式表示成信号流图形式，用全差分放大器替换其中的积分部分，最后集成得到全差分有源跨阻带阻滤波器[13-14]．文中给出了六阶Chebyshev跨阻带阻滤波器的设计实例及其HSpice仿真结果．

1 信号流图法推导

图1为六阶带阻无源LC梯形滤波原型电路，图中标出了流经各元件的电流和各节点电压．根据欧姆定律和基尔霍夫定律，对表征LC梯形内部行为的数学方程进行模拟[9]，使模拟框图仅包括积分器、加法器和尺度运算，可以得到各元件电压和电流变量之间的关系，即

根据式(1)列出的各电压变量和电流变量的运算关系，可以得到表示这种关系的信号流图(signalflow-graph，SFG)，如图2所示，其中滤波器的输出为V3．

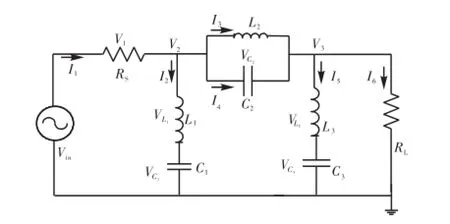
图1 六阶带阻无源LC梯形电路Fig.1 Six-order passive bandstop LC ladder filter

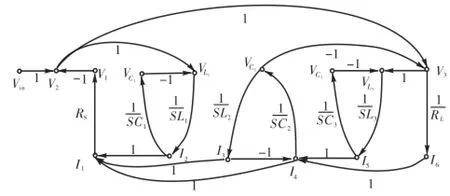
图2 六阶带阻滤波器的信号流图Fig.2SFG of six-order bandstop filter

图2 所示的信号流图中，上节点变量都为电压形式，下节点变量都为电流形式，为了用全差分运算放大器实现滤波器设计，即实现电压输入-电压输出，将所有的电流变量乘以一个比例电阻R，变成电压变量．变换后各电压变量之间的关系为

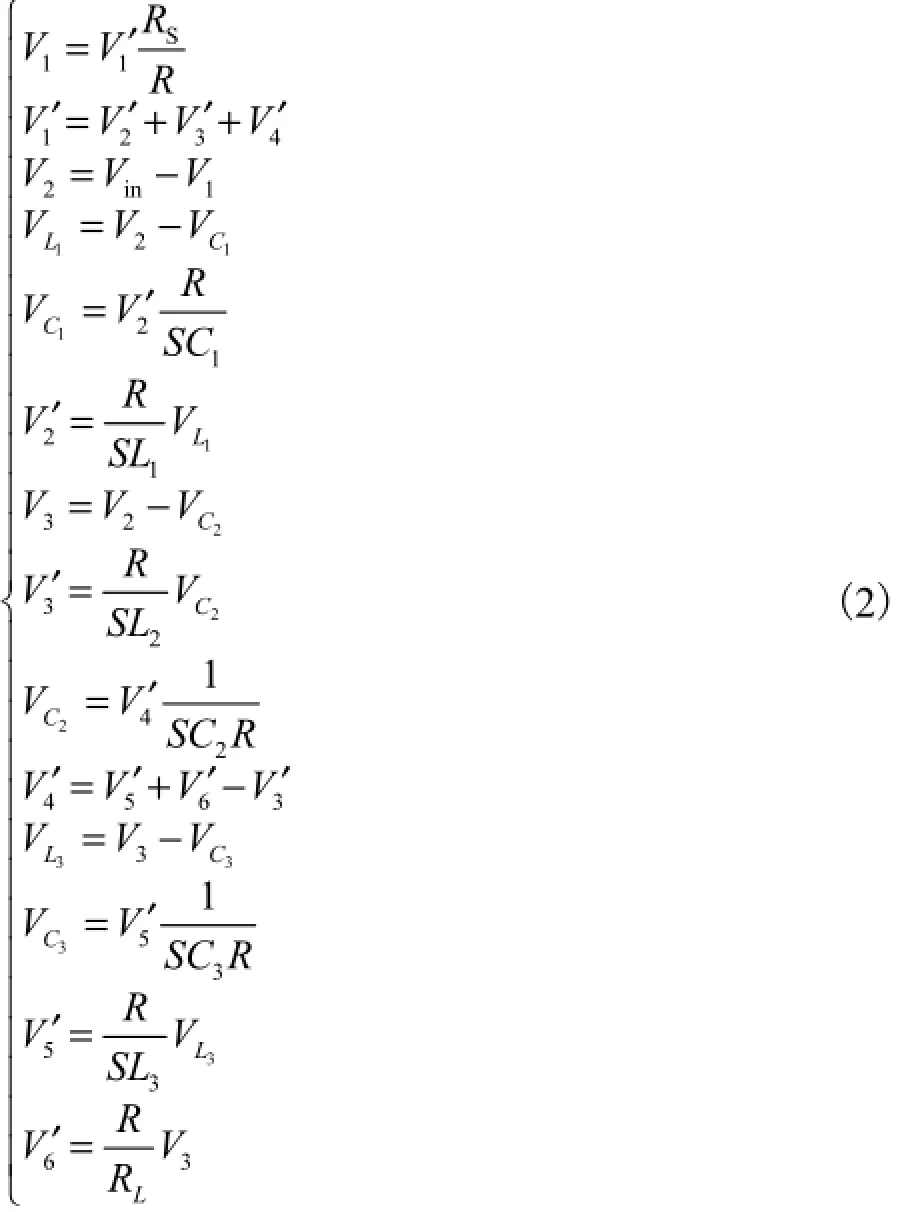
相应的信号流图如图3所示．根据图3信号流图所表示的各节点电压的运算关系式，可得到全差分运算放大器的输入输出关系，将这些运算关系利用节点关系进行综合，同时将电压源Vin与串联电阻Rs变换为等效的电流源与并联电阻Rs，就可得到集成全差分RC跨阻带阻滤波器，如图4所示．

图中所有的电阻值都取1Ω，则电容值满足关系C′1=C′2=C1，C′3=C′4=L1，C′5=C′6=C2，C′7=C′8= L2，C′9=C′10=C3，C′11=C′12=L3．

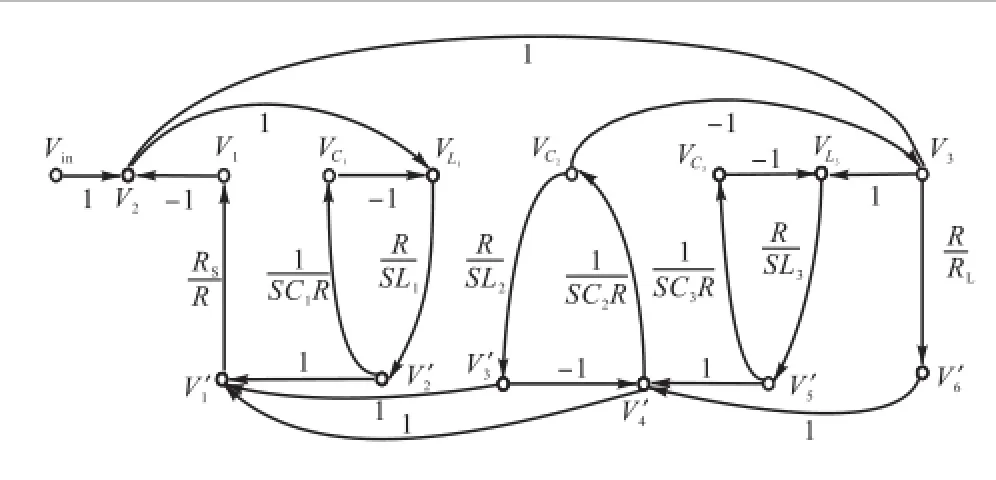
图3 变换后的信号流图Fig.3 Converted SFG

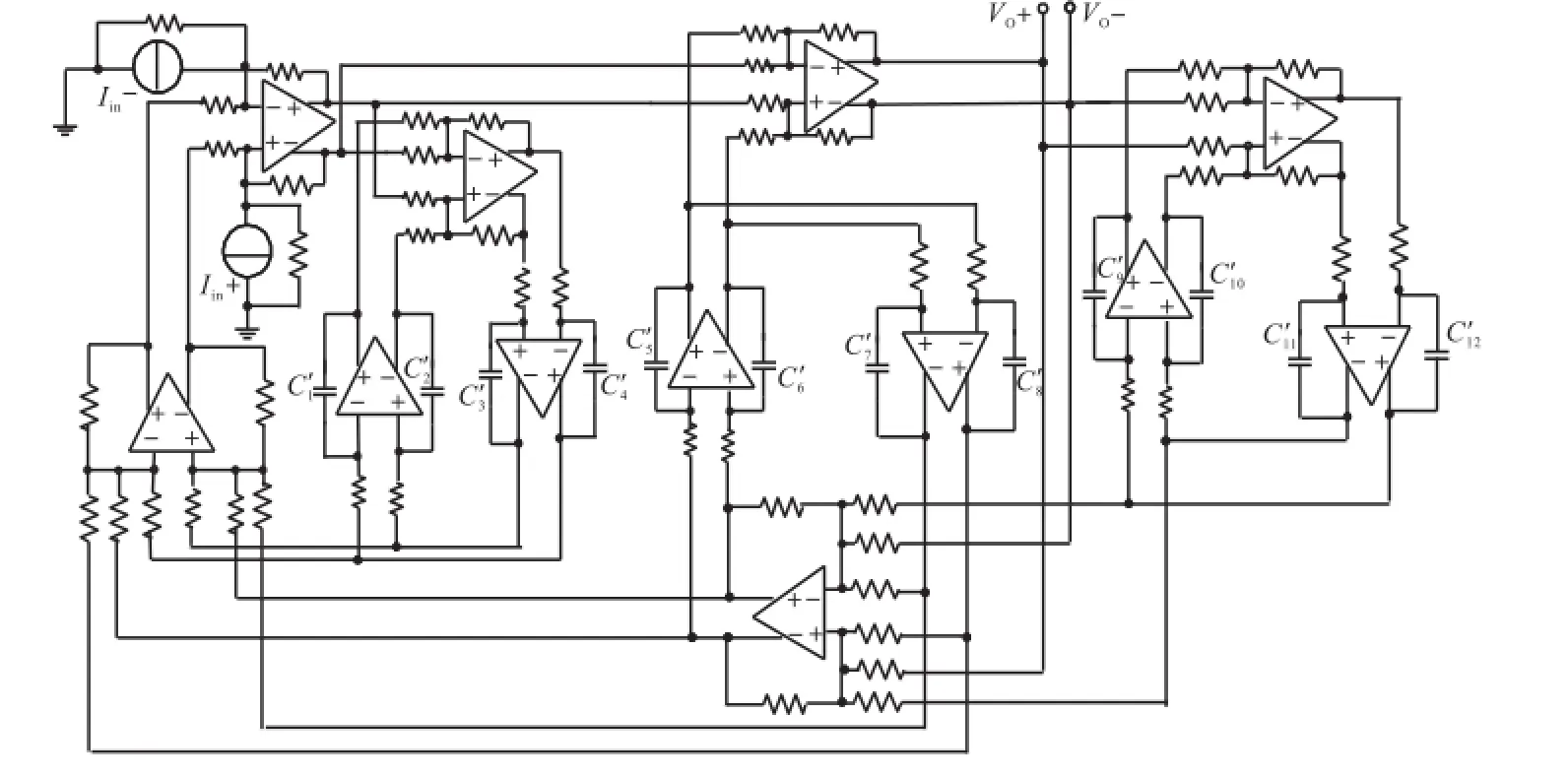
图4 六阶集成有源跨阻带阻滤波器Fig.4 Six-order integrated active transimpedance bandstop filter

2 设计实例

为了更好地阐述同时验证上述的跨阻带阻滤波器设计方法，设计1个滤波器，并对其进行仿真验证.

所设计带阻滤波器的技术指标如下：

(1)下通带截止频率lf=0.4,MHz，上通带截止频率uf=2.5,MHz；

(2)阻带下限截止频率slf=0.67,MHz，阻带上限截止频率suf=1.5,MHz；

(3)通带允许的最大衰减maxA=0.5,dB，阻带允许的最小衰减minA=20,dB；

(4)通带最大波动为0.5,dB，双端接载RS=RL= 10,kΩ．

进行频率转换，可得到低通滤波器的LC原型电路，如图5所示．

根据低通到带阻的转换关系，可得到无源带阻滤波器原型电路，如图6所示，其中各元件值已经标出．

运用前面介绍的方法进行电路综合，同时进行电路参数的反归一化，即可得到有源RC带阻滤波电路，如图7所示，图中所有电阻值都是10,kΩ，输出为OV+和OV-．

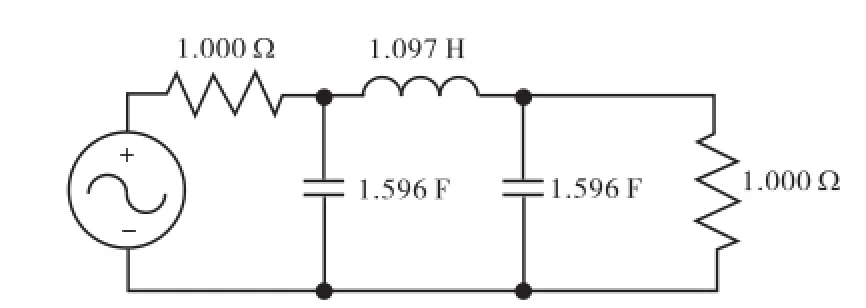
图5 无源低通滤波器原型电路Fig.5 Prototype of passive lowpass filter

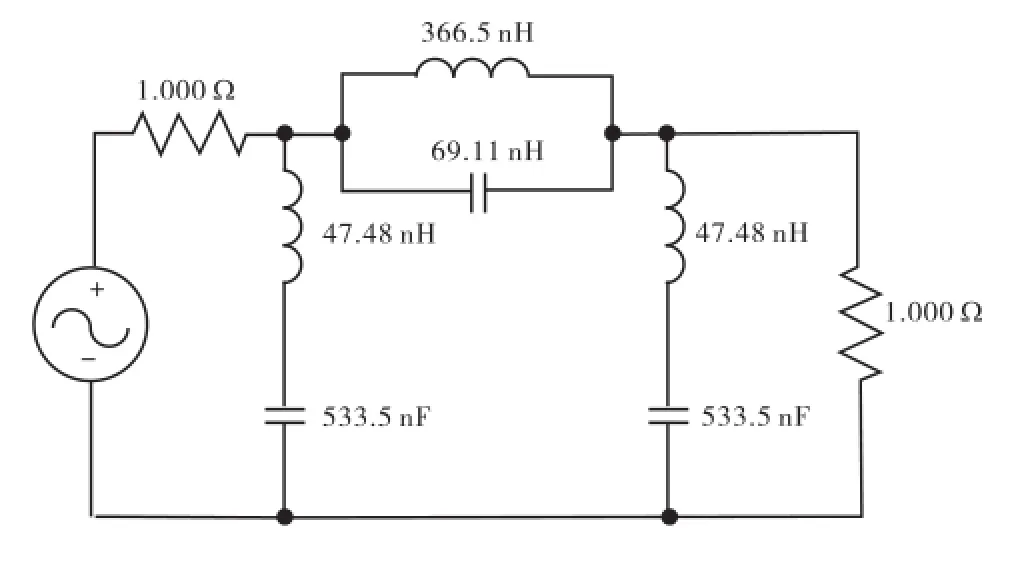
图6 无源带阻原型电路Fig.6 Prototype of passive bandstop filter

图7 六阶集成有源跨阻带阻滤波器Fig.7 Six-order integrated active transimpedance bandstop filter

3 仿真结果

本文采用的是LMH6551全差分积分器模型．接下来对图7建立网表，用Hspice进行仿真，得到滤波器的幅频特性如图8所示．图8(a)表示0～5,MHz范围内的幅频特性，图8(b)和(c)分别表示下通带和上通带内的幅频特性．

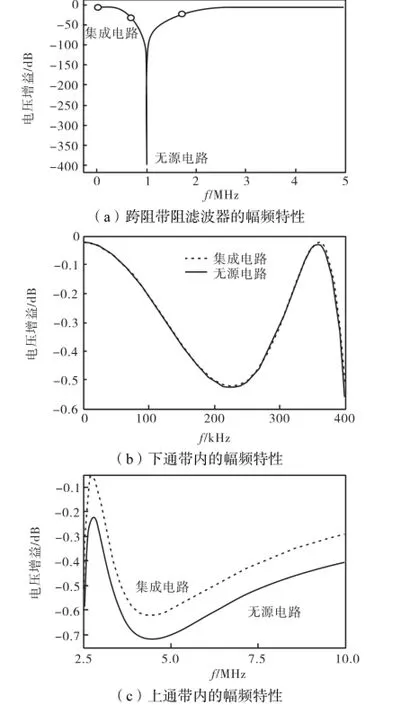
图8 仿真结果Fig.8 Simulated results

图8 (a)中，阻带的中心频率是1.0,MHz，在0.67,MHz处的衰减是35.4,dB，在1.5,MHz处的衰减是35.3,dB，满足技术指标阻带衰减最小为20,dB的要求．全集成有源RC六阶带阻滤波器的幅频特性曲线和无源LC六阶带阻滤波器的特性曲线基本重合，差别仅在于阻带中心处理想滤波器的衰减为无穷大，而设计得到的集成有源跨阻带阻滤波器在此处的衰减为160,dB左右，产生这种差别的原因主要是实际运放的增益特性不完全满足全极点模型．图8(b)和(c)分别是带阻滤波器下通带和上通带的幅频特性，可以看出下通带最大波动小于0.5,dB，上通带最大波动小范围内在0.5～0.6,dB之间，多数频段内小于0.5,dB，基本满足通带波动最小为0.5,dB的技术指标．

4 结 语

本文提出了跨阻带阻滤波器的设计方法．利用双端接载的无源LC梯形网络响应对元件变化敏感度低的特点，以无源LC梯形网络为基础，运用运算模拟法集成得到的有源跨阻带阻滤波器带阻中心频率为1.0,MHz，其设计方法简单、调节方便且保留了LC梯形网络敏感度低的特性，实验结果满足技术指标，具有很好的滤波特性，充分说明了该结构及设计方法的准确性．

［1］ Ibrahim M A. The inverting second-generation current conveyor in implementation of transimpedance-modetow-thomas filter[C]//International Conference on Communication，Computer and Power(ICCCP’09). Muscat，Oman，2009：179-182.

［2］ Minaei S. A new high performance CMOS third generation current conveyor(CCIII)and its application [J]. Electrical Engineering，2003，85(3)：147-153.

［3］ Ibrahim M A. A transimpedance type multifunction filter suitable for MOSFET-C technology[C] // 5th International Conference on Electrical and Electronics Engineering(ELECO’2007). Bursa，Turkey，2007.

［4］ Carlosena A，Cabral E. Novel transimpedance filter topology for instrumentation[J]. IEEE Transactions on Instrumentation and Measurement，1997，46(4)：862-867.

［5］ Chandra G，Tadeparthy P，Easwaran P. Single amplifier bi-quadratic filter topologies in transimpedance configuration[J]. IEEE Transactions on Circuits and SystemsⅡ：Express Briefs，2008，55(6)：502-506.

［6］ Minaei S，Topcu G，Cicekoglu O. Transimpedance type multifunction filter without using any external passive elements[C] //The 2002 45th Midwest Symposium on Circuits and Systems. Tulsa，Oklahoma，2002：633-636.

［7］ Chandra G，Tadeparthy P，Easwaran P. High Order Transimpedance Filter with a Single Operational Amplifier：US，10/711724[P]. 2004-09-30.

［8］ 杨志民，袁助国，徐守堂. 采用Q倍增结构的有源RC高Q二阶带阻滤波器[J]. 电子学报，1992，20 (9)：96-99.

Yang Zhimin，Yuan Zhuguo，Xu Shoutang. Second order high-Q active RC bandstop filter[J]. Acta Electronica Sinica，1992，20(9)：96-99(in Chinese).

［9］ Orchard H J. Inductorless filters[J]. Electronics Letters，1966，12(6)：224-225.

［10］ 滕建辅，王明国，刘宗良，等. 低敏感度大动态范围全集成滤波器的设计[J]. 电路与系统学报，2009，14(5)：122-125. Teng Jianfu，Wang Mingguo，Liu Zongliang，et al. Design of low sensitivity high dynamic range fullintegrated filters[J]. Journal of Circuits and Systems，2009，14(5)：122-125(in Chinese).

［11］ Manetti S，Piccirilli M C. Log-domain filter design based on impedance scaling of LC ladder structures[J]. Circuits Systems and Signal Processing，2011，30(2)：371-389.

［12］ Kontogiannopoulos N，Psychalinos C. Log-domain filtering by simulating the topology of passive prototypes [J]. IEEE Transactions on Circuits and Systems Ⅰ：Regular Papers，2005，52(10)：2043-2054.

［13］ Zhang B J，Yang Y T，Zhang H J. A fully balanced fifth-order low-pass chebyshev filter based on quasifloating gate transistors[C]// IEEE Conference on Electron Devices and Solid-State Circuits. Hong Kong，China，2005：537-540.

［14］ Perry D，Roberts G W. The design of log-domain filters based on the operational simulation of LC ladders [J]. IEEE Transactions on Circuits and Systems Ⅱ：Analog and Digital Signal Processing，1996，43(11)：763-377.

Design Method of Integrated Transimpedance Bandstop Filter

Li Qiang1，Xuan Xiuwei2，Li Kun2，Teng Jianfu1,2
(1. School of Electronic and Information Engineering，Tianjin University，Tianjin 300072，China；2. School of Electronic and Information Engineering，Tianjin University of Technology，Tianjin 300384，China)

As a unique form of filter, transimpedance filter plays an important role in integrated circuits. Based on a LC ladder prototype, a design method of integrated transimpedance bandstop filter was proposed. First, the variables of LC elements were presented by state variables. Then the relationship was expressed by signal flow graph (SFG). With fully differential operational amplifier as their basic elements, the structure of bandstop filter was derived by operational simulation methods. To show the design process, an example of a six-order Chebyshev transimpedance bandstop filter was presented. Its Hspice simulation results were given. The simulation results show that the designed transimpedance filter can meet the required specifications and has good filtering performance.

transimpedance；bandstop filter；passive ladder network；active filter；operational simulation

TN713

A

0493-2137(2013)07-0585-05

DOI 10.11784/tdxb20130703

2011-12-18；

2012-02-10.

国家自然科学基金资助项目(60802049).

李 锵（1974— ），男，博士，教授，liqiang@tju.edu.cn．

轩秀巍，xiuweixuan@tju.edu.cn.