基于性能的重力坝随机地震反应概率特征

张社荣，王 超，孙 博

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

基于性能的重力坝随机地震反应概率特征

张社荣，王 超，孙 博

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

基于概率分析方法，对水工重力坝动力反应参数进行了随机描述，提出了重力坝随机地震反应的概率特征分析方法，并得到了其概率分布特征和规律．首先统计分析了国内典型重力坝场区地震危险性资料，得出了场区水平地震加速度与年超越概率的近似关系式，为概率地震反应计算提供了基础；然后，以一定数量的强震波为随机动力输入，以工程中较为关注的动力特征响应量为工程反应参数，按照非线性动力响应分析、不同烈度下动力反应参数最值统计规律和概率分布特征假设检验以及工程反应参数的年超越概率这3个层次进行重力坝的概率地震反应及其概率特征分析．结果表明：在设计关心的地震强度范围内，以水平地震加速度表征的地震危险性曲线近似服从幂指数关系；经检验，选定的重力坝工程反应参数服从对数正态的概率分布特征；计算得到的年超越概率曲线可以合理评估重力坝在地震中发生各种破坏的可能性．

水工结构；重力坝；概率地震分析；地震危险性分析；性能设计

在工程结构全生命周期设计中，工程师需要了解结构在未来遭受不同强度地震作用下的破损概率．然而由于地震作用的随机性，传统的某几条“设计地震”作用下的确定性分析无法实现这一目标，难以揭示其地震反应的客观随机规律；另一方面，一个合理的分析模型应该能够反映结构在地震作用下真实的工作性态，给出在不同概率水平地震作用下结构的动力特性，于是，越来越多的学者开始从概率的角度对基于性能(performance-based)的结构抗震理论进行研究，不同强度地震下结构的动力性能及其规律也成为设计者关心的问题．

基于性能的结构抗震，最先由建筑结构领域开始发展，其基本思想是使被设计的建筑物在使用期间满足各种预定功能或性能目标要求．也可以定义为基于不同设防水准地震作用，达到不同的性能目标．Bazzurro[1]以概率方法为基础研究了建筑结构的地震需求模型；美国太平洋地震工程研究中心(PEER)提出了基于性能地震工程(performance-based earthquake engineering，PBEE)的框架[2]，其目标之一就是计算结构在给定场地条件下，结构需求超越特定水平的年平均超越概率．陈厚群等[3]在水工结构抗震领域率先运用概率分析方法探讨了水电工程抗震设防的概率水准和地震作用的概率模型，为基于性能的水工抗震提供了基础；近年来，涂劲等[4]对小湾拱坝在不同概率水平地震作用下的抗震安全进行了分析，给出其在不同水平地震作用下的抗震超载安全度；沈怀志等[5]和寇立夯等[6]也研究了基于性能的高坝抗震中的一些关键问题．

笔者在PBEE框架内对水工重力坝地震反应的概率特征进行分析研究．首先对国内8座典型重力坝工程场地危险性资料进行统计分析，得到了坝址水平地震加速度与年超越概率的近似关系式；然后采用概率分析方法，以工程中关注的坝体关键部位动应力、位移和损伤能耗为反应参数，得到了随机地震下其动力反应的概率分布特征和超越概率曲线．这对于合理评估重力坝在地震中发生各种破坏的可能性，以便选择合理的抗震设计与加固措施来提高其抗震性能具有重要意义，也可为地震条件下的重力坝安全风险率分析提供计算基础．

1 概率地震反应分析方法

为了得到重力坝的概率地震反应，需要进行两方面工作：一是分析工程场地的地震危险性曲线；二是确定不同强度地震下，重力坝工程反应参数(engineering demand parameter，EDP)的分布规律及其超过给定限值的概率．

基于场地地震危险性分析的地震作用概率模型分析是由美国Cornell[7]于1968年提出的，由于该方法比较成熟，且文献[3]中也进行了详细讨论，本文不再赘述．下面给出重力坝动力反应参数的超越概率分析方法．文献[6,8]中多是基于地震烈度变量的超越概率表达式(见式（1)），但在我国《水工建筑物抗震设计规范》(DL 5073—2000)中，抗震计算中的地震荷载都是以水平峰值加速度的函数形式给出的，因此，为了在抗震设计中更为方便地理解和使用，本文给出水平地震加速度为变量的重力坝工程反应参数超越给定值的概率表达式．

动力条件下，记重力坝的反应参数小于给定值edp的概率为P(EDP＜edp)，则有[9]

式中h()P A为水平峰值加速度为ha的地震发生的年平均概率．于是，工程反应参数超过给定值的概率为

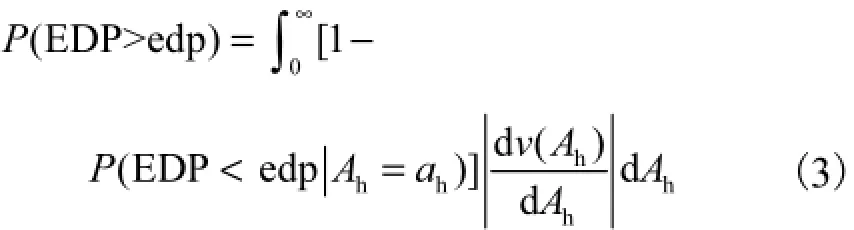
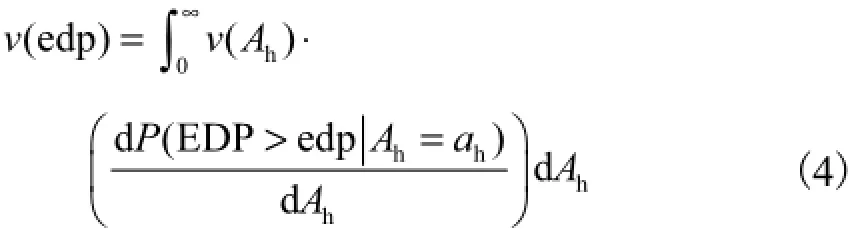
至此，便建立了重力坝动力反应参数超越概率分析的计算方法．

2 场区地震作用概率模型

重力坝场地设计地震加速度超越概率曲线是根据大坝场区的地震安全性评价得到的，这是进行场区地震动强度不确定性分析及结构概率地震反应分析的基础和依据．本文根据官地、金安桥等8座国内大型重力坝坝址区地震安全性评价的相关资料，研究工程场区地震危险性，对国内大型重力坝场区水平向地震峰值加速度与年超越概率的关系进行了简化，并给出了近似表达式．

基于一般的地震危险分析，工程地震加速度的年超越概率应是极值型曲线族，即类似图1中曲线1(丰满大坝场地水平向地震加速度的年超越概率理论曲线)所示．但对8座典型的水电站坝址区地震危险性曲线进行分析后可知，在设计关心的地震烈度范围(对应于100年基准期超越概率2%和50年基准期超越概率10%的地震)内，场地危险性曲线可以近似表达为图1坐标系下的直线段．例如，图1中丰满大坝的场地加速度年超越概率关注烈度范围的简化直线段是与其相应的理论曲线1基本吻合的．其余大坝也可以得出类似结论．

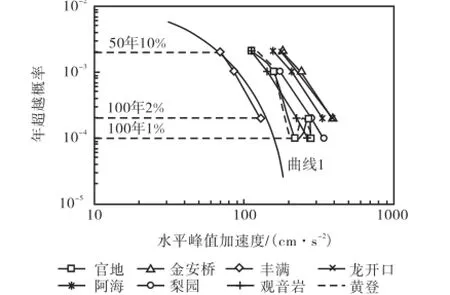
图1 典型重力坝场区水平峰值加速度的年超越概率曲线Fig.1 Annual probability of exceedance for peak ground acceleration in the dam construction area

另外，研究者也曾得到地震烈度和超越概率的简化关系式[11](该式亦为对数坐标系下的直线关系)为

式中：v(IM)为地震烈度的年超越概率；k0和k为经验常数，常取k=1～4之间的数值，与地理位置有关，可根据坝址区场地不同超越概率的地震动参数进行拟合．进一步地，本文根据地震烈度和水平地震系数的关系

给出以水平地震系数表达的水平地震加速度及其重现期的近似关系为

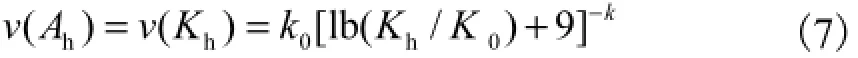
式中：0K为常数，可取为0.4；0k和k与式(5)中含义相同；hK为特定水平峰值加速度对应的水平地震系数．

3 重力坝分析模型及参数选取

3.1 结构模型及计算参数

某水电站挡水建筑物为碾压混凝土重力坝．如图2(a)所示，挡水坝段坝顶高程为1,334.00,m，建基面高程为1,192.00,m，正常蓄水位1,330.00,m，相应下游水位1,203.70,m，坝前泥沙淤积高程1,211.10,m．坝体碾压混凝土分为3个区域，各区域的材料参数见表1．坝址区50年基准期超越概率为10%、5%的基岩场地设计水平加速度峰值分别为0.114g和0.161g；100年超越概率2%的水平向地震峰值加速度为0.284g．

图2(b)为计算采用的有限元模型，地基范围为上、下游和深度方向均为2倍坝高(图中仅显示了局部范围地基的有限元模型)．计算采用四边形网格，坝体网格相对较小并向地基网格逐渐过渡．模型底部采用全约束，左右边界采用法向约束．

混凝土本构采用塑性损伤模型，碾压混凝土材料密度2,400,kg/m3，泊松比0.2，动弹性模量及抗拉、压强度见表1．地基为Ⅱ类岩基，采用无质量弹性地基模型进行模拟，弹性模量18,GPa，泊松比0.22，抗剪断参数f=1.12，c=1.40,MPa．岩体动弹性模量暂取静态值．

表1 混凝土的材料参数Tab.1 Material parameters of concrete

在动力计算中，地震动采取顺水流向和竖向同时由地基输入，动水压力采用Westergaard公式计算，Rayleigh阻尼因数根据结构前两阶频率计算．荷载组合为：上游正常蓄水位水压力+下游相应尾水位水压力+坝体自重+上游淤沙压力+坝基面扬压力+地震荷载．其中，坝前泥沙浮容重为6.0,kN/m3，淤沙内摩擦角为12°．

3.2 地震动输入的选取

用于数值分析的地震动时程包括实际强震记录和人工拟合地震时程2种，为了获取更多数据对结构地震响应做出更加合理的统计分析，研究中选用了30条地震波，包含10条实测波(中远场地震波，没有方向性)和20条采用三角级数法随机生成人工波(相位角随机)作为时程分析的激震荷载．具体的时程记录不再详细给出，图3给出了阻尼比为5%的30条地震记录的加速度反应谱与规范目标谱的对比情况．可以看出，实测波的谱值在不同的频段各有特点；随机生成人工波与规范目标谱的拟合情况良好．

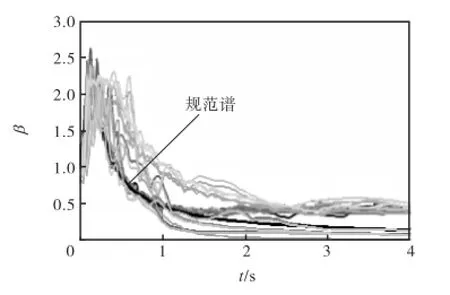
图3 地震波反应谱与规范谱对比Fig.3 Response spectra vs the normal spectrum of the waves

地面运动特征可用地震动强度指标表征，本文采用传统的峰值谱速度指标表征地震动强度特征，计算中将其峰值加速度缩放到设计关心的烈度水平，即分别调幅值为0.114g、0.161g和0.284g．另外，为了控制结构动力响应的极限状态，研究中计算了地震峰值为0.400g时的情况．

3.3 工程反应参数的选取

为了考察地震作用下的重力坝动力性态，了解结构在不同地震烈度地震下的响应分布特征，选取工程中较为关注的坝体下游折坡点主拉应力、坝踵主拉应力，坝顶顺水流向位移、坝顶沉降，坝体损伤和塑性能耗等响应量作为重力坝工程反应参数进行详细分析.

4 概率地震分析及性能评估

概率地震分析[12]可以用来计算结构需求超越特定水平的年平均超越概率以及评价结构在将来任意地震中的性能水准．针对重力坝分析实例，采用数理统计方法对计算结果进行分析．下面分3个层次对重力坝的概率地震反应统计特征和性能进行分析评估．

(1)在4个不同的地震烈度下进行多条确定性的地震波下坝体的非线性地震反应分析，得到结构的响应时程曲线，并从中分别提取重力坝结构相应动力反应量的最大值．

(2)统计所有的30组地震动激励下重力坝相应动力反应量最值参数，对这些数据的均值和对数标准差进行估计，得出其累积概率分布规律，并进行概率分布特征的假设检验．

(3)计算工程反应参数均值的年超越概率，并判断重力坝动力反应参数超过给定值的年平均超越概率，进而为工程师掌握随机地震作用下的重力坝动力性态提供依据．

4.1 不同地震水平下的确定性响应

将其峰值加速度缩放到设计关心的烈度水平，即分别研究调幅值0.114g、0.161g、0.284g以及0.400g时的情况．基于ABAQUS平台，采用塑性损伤模型来分析坝体混凝土在地震荷载作用下的非线性动力响应．以迁安地震波(计算历时15.0,s)激励下重力坝结构的响应为例进行阐述．图4～图6分别给出了迁安波下坝体动力反应参数的时程变化曲线．从图中可以看出，在一次确定性的迁安地震波激励下，重力坝非线性动响应符合一般规律．

图4 迁安波下坝体动应力反应时程曲线Fig.4 Stress vs time in dam under Qian’an earthquake wave

图5 迁安波下坝体位移反应时程曲线Fig.5 Displacement vs time in dam under Qian’an earthquake wave

图6 迁安波下坝体动力能耗反应时程曲线Fig.6 Energy dissipation vs time in dam under Qian’an earthquake wave

应力方面，随着地震动峰值的增大，坝体关键位置的动应力峰值均有所增大．坝体下游折坡处的主拉峰值应力由0.284g地震激励下的2.84,MPa增大到0.400g激励下的2.96,MPa，且峰值过后，由于应力重分布，单元应力维持在较低的水平．位移方面，随着地震动峰值的增大，坝顶位移峰值也随之增大．能耗方面，坝体动力能耗在地震过程中表现为不可逆的增大过程，损伤累积不断发展．

4.2 结构反应参数的概率分布特征

与迁安波分析类似，得到其他地震波作用下重力坝响应以后，统计不同烈度所有地震动激励(30条× 4组)下重力坝相应动力反应量最值参数，得出其累积概率分布曲线，进行概率分布的假设检验，确定其较优分布类型．表2给出了不同烈度下重力坝动力反应参数的统计值．为了确定样本统计数据的分布类型，常用的做法是：根据样本数据的概率密度分布(probability density function，PDF)特征以及累积概率分布(cumulative distribution function，CDF)特征，以一定的典型特征分布作为假设，然后进行假设检验，确定其是否符合良好．以下游折坡主拉应力的响应统计量为例，首先给出不同烈度下该反应参数的样本分布PDF和CDF特征，如图7和图8所示．

从图8中可以看出，在0.114g和0.161g地震作用下，坝体下游折坡的主拉应力超过相应区域动态抗拉强度2.3,MPa的概率基本在5%范围以内，即该区域破损的概率很小；而在0.284g和0.400g作用下，该区域超拉应力的概率分别可以达到80%和90%，即说明该区域基本上都会出现动力破损．

表2 不同烈度下重力坝动力反应参数的统计值Tab.2 Analysis results of the EDPs at different intensity levels

图7 坝体下游折坡主拉应力反应量统计直方图Fig.7 Histograms from statistics of the stress in the dam sloping at downstream

根据图8显示的分布特征，样本的累积分布显然是一个指数型分布．常见的指数型分布有很多种[13]，这里选取典型的正态(Normal)分布、对数正态(Log-Normal)分布、伽马(Gamma)分布以及威布尔(Weibull)分布作为假设分布进行检验．表3给出了其概率密度函数式及数字特征．

接着进行假设检验．根据数理统计理论，通过PP图(根据变量的累积比例与指定分布的累积比例之间的关系所绘制的图形)和Q-Q图(变量数据分布的分位数与所指定分布的分位数之间的关系曲线)可以检验数据是否符合指定的分布．本文根据Q-Q图的思想，对样本数据进行对数正态检验，如图9所示，对数正态分布与结构反应的样本值拟合良好．

图8 不同烈度下结构反应参数的条件概率累积分布特征Fig.8 Cumulative distribution functions of the EDPs at different intensity levels

表3 假设分布的概率密度函数式及其数字特征Tab.3 Probability density function and associated parameters of certain probability distributions

类似地，得到不同烈度下重力坝坝踵主拉应力、动位移和动能耗反应的概率分布特征．这里不再详细列出．统计检验的结果表明，结构动位移和动能耗的反应样本的累积概率分布也近似服从对数正态特征．

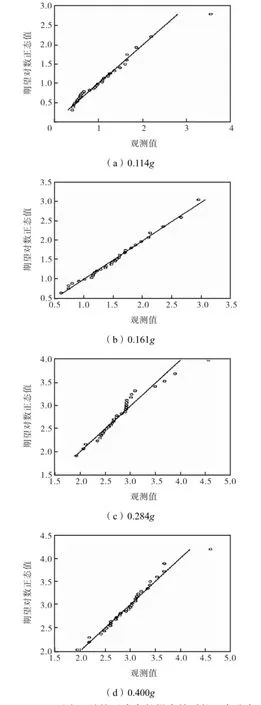
图9 不同烈度下结构反应参数样本的对数正态分布假设检验Fig.9 Probability plot of fitted Log-Normal PDF for the EDPs at different intensity

4.3 基于概率地震的重力坝动力性能评估

对本文算例，由场地地震危险性分析得到算例工程坝址地震烈度(IM)和超越概率的近似关系为

即有k0=0.005 2,k=2.981．将该参数代入式(7)，可得水平地震加速度的年超越概率为

将式(9)代入工程反应参数的超越概率的计算式(4)中，参照文献[6]中的做法进行简化计算，可以得到相应反应参数的年超越概率．以算例重力坝地震反应参数中的下游折坡主拉应力和坝顶顺水流向位移参数为例，求解相应的工程反应参数年超越概率曲线，如图10所示．计算中标准差取为不同地震水平下反应参数标准差的对数均值．

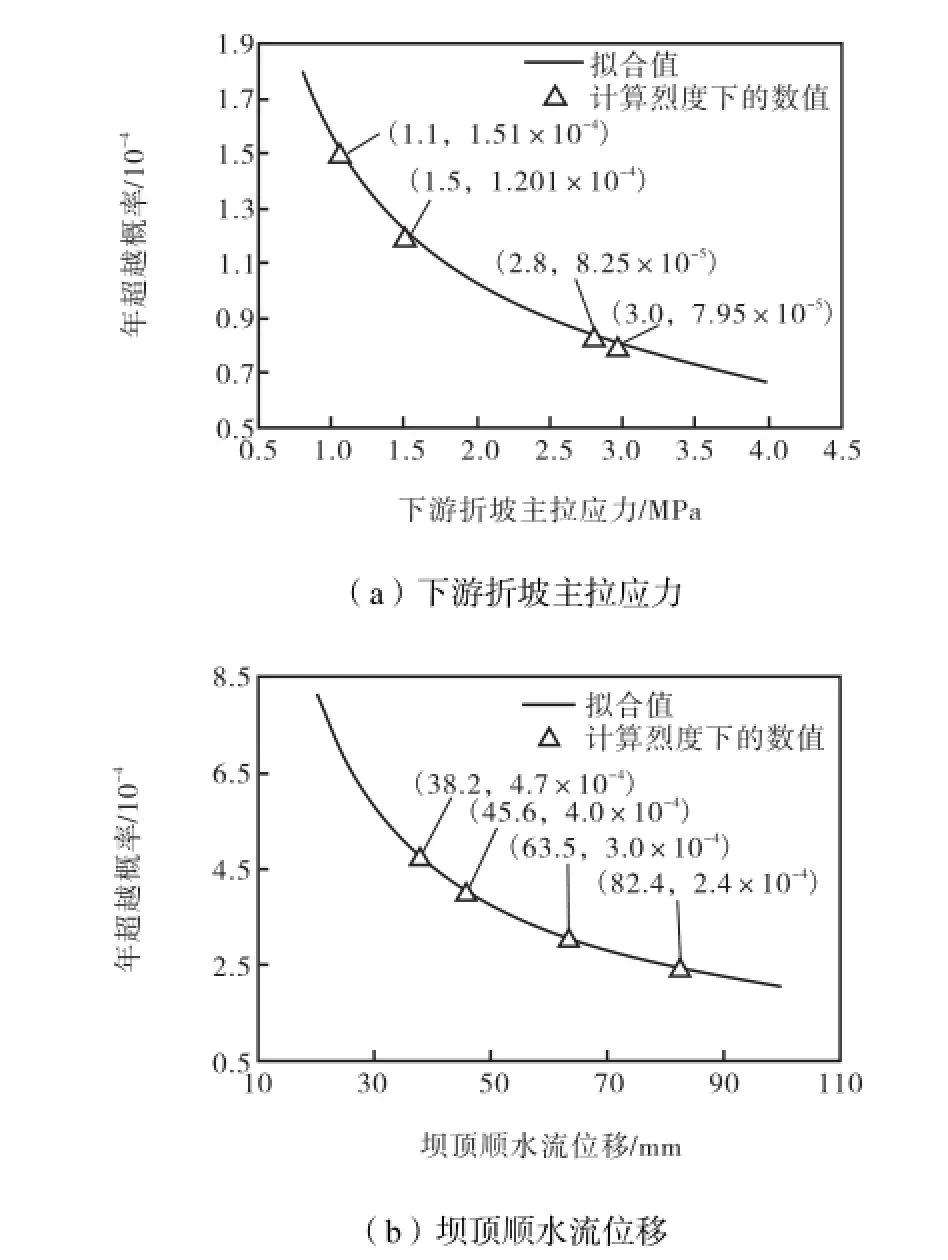
图10 重力坝反应参数的年超越概率曲线Fig.10 Mean annual probability of exceedance for the EDPs of the dam

由图10可知工程反应参数超过给定值的年平均超越概率．如：坝体下游折坡处的主拉应力超过动态抗拉强度2.30,MPa的年超越概率约为9.45×10-5；其坝顶位移峰值超过100,mm的年超越概率约为2.05×10-4．

5 结 论

(1) 经过统计分析，在工程关注的地震水平范围，以水平地震加速度表征的重力坝场地地震危险性曲线也近似服从幂指数关系，即表现为双对数坐标系下的直线段．

(2) 按照本文提出的3个层次的重力坝地震反应的概率特征分析方法，在不同地震水平下，本文选取的重力坝动力反应参数的累积概率分布均近似服从对数正态分布特征．

(3) 通过分析基于概率意义的地震反应超越概率曲线可以定量了解重力坝在不同地震烈度情况下超越一定工程限值的概率，这对合理评估重力坝在地震中发生各种破坏的可能性具有重要作用．

［1］ Bazzurro P. Probabilistic Seismic Demand Analysis[D]. California：Stanford University，1998.

［2］ Porter K A. An overview of PEER’s performance-based earthquake engineering methodology[C]// 9th International Conference on Application of Statistics and Probability in Civil Engineering(ICASP9). San Francisco，California，USA，2003：973-980.

［3］ 陈厚群，侯顺载，梁爱虎. 水电工程抗震设防概率水准和地震作用概率模型[J]. 自然灾害学报，1993，2(2)：91-98.

Chen Houqun，Hou Shunzai，Liang Aihu. Probabilistic level fortification against earthquake and probabilistic models of seismic actions for hydraulic projects[J]. Journal of Natural Disasters，1993，2(2)：91-98(in Chinese).

［4］ 涂 劲，陈厚群，张伯艳. 小湾拱坝在不同概率水平地震作用下的抗震安全性研究[J]. 水利学报，2006，37(3)：278-285.

Tu Jin，Chen Houqun，Zhang Boyan. Seismic safety of high arch dam in Xiaowan Project under the action of earthquakes with different exceeding probabilities[J]. Journal of Hydraulic Engineering，2006，37(3)：278-285(in Chinese).

［5］ 沈怀至，金 峰，张楚汉. 基于功能的混凝土重力坝抗震风险模型研究[J]. 岩土力学，2008，29(12)：3323-3328.

Shen Huaizhi，Jin Feng，Zhang Chuhan. Performancebased seismic risk analysis model of concrete gravity dams[J]. Rock and Soil Mechanics，2008，29(12)：3323-3328(in Chinese).

［6］ 寇立夯，金 峰，王进廷. 基于概率的混凝土重力坝地震反应分析[J]. 水力发电学报，2009，28(5)：23-28.

Kou Lihang，Jin Feng，Wang Jinting. Probability-based seismic response analysis of concrete gravity dams[J]. Journal of Hydroelectric Engineering，2009，28(5)：23-28(in Chinese).

［7］ Cornell C A. Engineering seismic risk analysis [J]. Bulleting of the Seismological Society of America，1968，58(5)：1583-1606.

［8］ 曾志和，樊 剑，余倩倩 基于性能的桥梁结构概率地震需求分析[J]. 工程力学，2009，29(3)：156-162.

Zeng Zhihe，Fan Jian，Yu Qianqian. Performancebased probabilistic seismic demand analysis of bridge structures[J]. Engineering Mechanics，2009，29(3)：156-162(in Chinese).

［9］ Tothong P，Cornell C A. Probabilistic Seismic Demand Analysis Using Advanced Ground Motion Intensity Measure，Attenuation Relationships，and Near-Fault Effects[R]. Berkeley，USA：Pacific Earthquake Engineering Research Center(PEER)，University of California，2006-11.

［10］ 李振富，张社荣，郭怀志. 水平地震系数的概率特性估计及应用[J]. 天津大学学报，1993，26(l)：105-109.

Li Zhenfu，Zhang Sherong，Guo Huaizhi. The probabilistic evaluation of the horizontal earthquake coefficient and its application[J]. Journal of Tianjin University，1993，26(l)：105-109(in Chinese).

［11］ Cornell C A，Jalayer F，Hamburger R，et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering，2002，128(4)：526-532.

［12］ Shome N，Cornell C A，Bazzurro P. Earthquakes，records，and nonlinear responses [J]. Earthquake Spectra，1998，14(3)：467-500.

［13］ Kelliher D，Sutton-Swaby K. Stochastic representation of blast load damage in a reinforced concrete building [J]. Structure Safety，2012，34(1)：407-417.

Probabilistic Characteristics of the Performance-Based Seismic Response of Concrete Gravity Dams

Zhang Sherong，Wang Chao，Sun Bo
(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

Based on the probabilistic seismic analysis method, the stochastic description of seismic response parameters was presented, the probabilistic analysis method of gravity dam was put forward, and the probability distribution laws were obtained. Firstly, the statistical data for seismic hazard was analyzed, based on which the approximate relationship between horizontal earthquake coefficient and exceeding probabilities was obtained, which served as a basis for probability seismic response calculation. Then，three levels of procedure were presented for seismic response and its probability characteristic analysis，including the following respects：nonlinear dynamic response was computed from a series of deterministic response analysis with three loading intensity levels；probability distribution of engineering demand parameter was assumed and regression analyses were conducted；the annual probability caves were estimated to be the exceedance of various engineering demand parameters. The results show that seismic risk curve approximately obeys the power exponent relationship in our concern area，and that the log-normal probability distribution characteristics for the selected parameters of gravity dam are acceptable. The possibility of each failure of the gravity dam can be reasonably evaluated from the exceeding probability curves in the earthquake.

hydraulic structure；gravity dam；probabilistic seismic analysis；seismic hazard analysis；performancebased design

TV312

A

0493-2137(2013)07-0603-08

DOI 10.11784/tdxb20130706

2012-11-27；

2012-12-28.

国家自然科学基金创新研究群体科学基金资助项目(51021004)；天津市应用基础与前沿技术研究计划资助项目(13JCYBJC19400)．

张社荣（1960— ），男，博士，教授，tjuzsr@126.com.

王 超，tjudam@126.com.