考虑土体软化的隧道盾构掘进界面稳定性分析

张义同，朱 龙，宁加星

(1. 天津大学机械工程学院，天津 300072；2. 天津市地下铁道集团有限公司，天津 300240)

考虑土体软化的隧道盾构掘进界面稳定性分析

张义同1，朱 龙1，宁加星2

(1. 天津大学机械工程学院，天津 300072；2. 天津市地下铁道集团有限公司，天津 300240)

岩土工程中的许多土体有应变软化行为，这种软化行为能导致应变局部化，进而对土体的稳定性有重要影响．首先研究饱和砂土的排水平面应变压缩试验的剪切带的形成，进行数值分析，预测了实验现象．然后，考虑土体应变软化盾构掘进面失稳的影响，对深埋隧道的盾构掘进进行三维数值分析，对比分析渗流条件下应变硬化模型和应变软化模型以及应变软化条件下考虑渗流与未考虑渗流模型之间的区别．分析表明，土体应变软化更容易导致盾构掘进界面失稳，使得开挖面的极限支护压力和地表沉降增大、塑性区扩展比没有应变软化的土体更大．探讨了诸如内摩擦角、黏聚力等土质应变软化参数的变化对盾构掘进界面稳定性的影响，发现内摩擦角软化的影响较大，黏聚力次之．最后，对天津地铁9号线的一段盾构掘进进行了模拟，其结果与工程实测数据相吻合．

砂土；应变软化；应变局部化；剪切带；盾构；掘进界面失稳

随着国内盾构施工市场的扩大，盾构施工的土层条件及掘进环境等更为复杂多样，国内的盾构施工中出现了许多问题，其中较为突出且城市隧道施工最为关心的是施工对周围地基造成的过大影响[1-3]，而首当其冲的研究就是开挖面的稳定性．以往对盾构掘进面稳定性都是按传统的弹塑性理论来分析的，还没有考虑应变软化对盾构掘进面稳定性的影响．应变局部化是应变软化土体破坏时其应变或变形集中于某局部狭窄区域内的一种现象(如剪切带)，而传统的弹塑性理论由于峰值后区的负斜率，导致增量应力-应变矩阵出现奇异或负定，从而使得数值解变得不稳定或者不可解[4-6]，因而应变局部化扩展理论与传统的塑形区扩展理论有很大的区别[7]，在岩土力学与工程中，应变局部化和剪切带等问题已成为研究的热点问题之一[8]．

对于应变软化问题，国内外许多学者进行过研究．Brown等[9]较早对Hock-Brown介质中的应变软化行为进行分析，但因忽略了塑形区弹性应变的变化，得到的圆形洞室位移量值存在较大误差；Alonso等[10]采用传统弹塑形理论，通过求自相似解的方法，分析了圆形洞室问题在应变软化介质中的底层反应曲线以及软化区与参与强度区的范围．Alshibli等[11]制作了聚碳酸脂组合模具，在平面应变状态下对不同粒径的砂土进行实验，研究砂土试样的密度、围压以及砂土类型对其应力-应变关系曲线的影响．哥伦比亚大学2006年用Nevada砂土做了平面应变压缩实验[12]，清楚记录了砂土试件在轴向压缩和围压作用下剪切带出现和扩展的整个过程．

尽管国内外对应变软化进行了很多的研究分析，但考虑土体应变软化对盾构隧道掘进面的稳定性的分析还没有．笔者探讨考虑土体应变软化和地下水渗流对盾构隧道掘进面稳定性的影响，为了考察其数值方法关于土质应变软化行为模拟的可靠性，首先模拟了平面应变条件下砂土试件中的应变局部化的形成与扩展，并与实验结果进行对照；然后考虑应变软化和渗流对隧道掘进面稳定性的影响，并分别与未考虑软化和未考虑渗流的情况对比；最后分析土质应变软化参数对盾构掘进界面稳定性的影响，为今后国内地铁盾构施工对周围土体扰动影响程度的预测提供工程依据．

1 平面应变条件下砂土应变局部化

应变局部化可以看成一个分岔问题，但是对这类分岔问题而言，只有两相解才是其稳定的分岔解[13]，Papamichos等[14]和Vardoulakis[15]曾分别进行应变局部化判别准则的分析，但均未对分叉后的力学性状进行探讨．图1为哥伦比亚大学2006年用Nevada砂土所做的平面应变压缩实验的局部化照片．

图1 砂土试件的应变局部化照片Fig.1 Photos of strain localization in sand

图2 为砂土试件应变局部化模型．图中：Tc为围压；“+”标识的区域为应变局部化带，即剪切带．

图2 砂土试件的应变局部化模型Fig.2 Strain localization model of sand specimen

多相平衡要求在各自域内满足如下平衡方程(不考虑体积力情况下)，即

式中：Div为初始构形下的散度算子；π为第1 Piola-Kirchhoff应力张量．

跨越相变界面的跳跃条件[13]为

式中：N为初始模型中垂直于相变界面的单位向量，N=[N, N,N]T；W为应力功函数，满足

123

TAB和EAB分别是第2 Piola-Kirchhoff应力张量T和Green应变张量E的分量；f的定义为

跨越相变界面的位移必须是连续的，这意味着跳跃函数[]F可写为

式中⊗表示张量积．

跳跃条件式(3)也称为Maxwell关系，它表示Eshelby力在跨越两相界面处的连续性．

Zhang等[13]对这种实验进行了解析分析，求出了应变局部化的两相解，准确预测出了这种现象．以下对同一问题进行数值模拟．

砂土的材料取文献[13]中的F-75中的第4组砂F4砂为模型材料，在弹性阶段，材料的本构关系为线弹性，应变软化模型参数如表1所示．其中内摩擦角从48.2°软化到35°，剪胀角从18°软化到10°．

表1 砂土材料参数Tab.1 Parameters of sand materials

网格划分如图3所示，共划分900个单元．边界条件如下：在试样两端施加常速率1.5×10-8,m/s以给定位移，为了模拟砂土的平面应变状态，在模型前后两侧(即y=0,m和Y=0.02,m 2个面)约束y向位移．同时为了剪切带得以启动，在试样上设置一个缺陷．

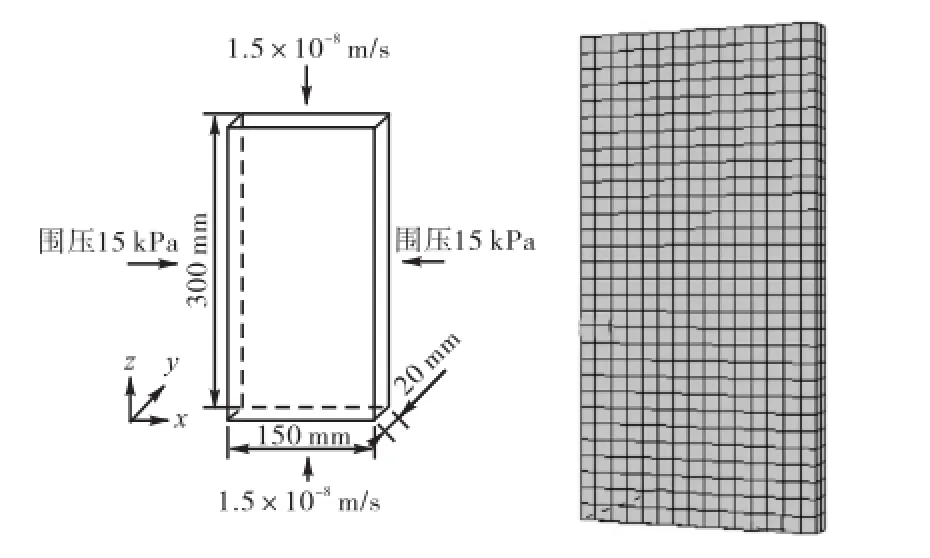
图3 数值模拟的砂土试样Fig.3 Sand specimen for numerical simulation

数值计算得到剪切带出现时的网格变形如图4所示，图中可以观测到一条明显的剪切带．在试样应变软化的过程中，剪切带逐渐得到了充分的发展．图4也给出了一个缺陷在不同位置时剪切带的成型现象.

对图4中的剪切带倾角进行测量，通过网格法进行边长计算，可得剪切带的切向与水平方向的夹角大致为58°．与图1比较，发现2个图基本吻合．

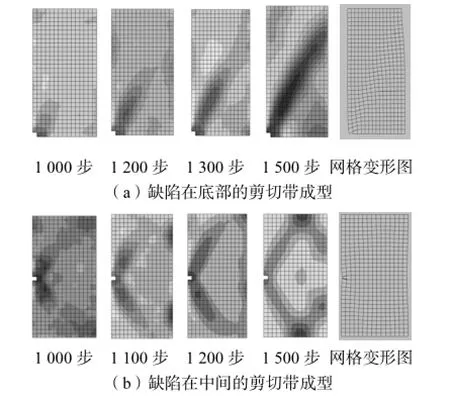
图4 试样网格Fig.4 Mesh of the specimen

2 盾构隧道掘进界面土体应变局部化的扩展

2.1 计算模型

考虑到目前我国相继出现很多大直径的隧道，计算土体模型如图5所示．取土体总长100,m，宽50,m，总高65,m，隧道直径为10,m，隧道埋深20,m，隧道下方取35,m，掘进面位于土体中部．水位面在地表下10,m处．模型的坐标如下：y轴沿隧道轴线，z轴垂直于地面．考虑土体模型对称性，对其1/2进行网格剖分，如图5所示．其边界约束如下：①在对称面上(即x=0面)约束x向位移；②在边界x=50,m面上约束x向位移，在y=0,m及y=100,m面上约束y向位移，z=0,m面上约束z向位移；管片为C50的钢筋混凝土弹性材料，厚度35,cm，采用shell单元模拟[16]．

图5 隧道计算模型Fig.5 Calculation model of tunnel

本文中衬砌与土体之间采用无间隙连接，衬砌瞬时支护．当衬砌刚度较小时，其洞壁周围会出现不同程度的塑性区．这些塑性区和土体塑性区连在一起，不便于观察．为了更好地观察开挖面前方塑性区扩展情况，本文在模拟中，对衬砌的刚度设置较大，同时不考虑土体的流变特性的影响．本构模型采用软件中自带的应变硬化-软化模型．

2.2 渗流条件下砂土硬化与软化对比分析

2.2.1 隧道模型材料参数

土体材料为砂土，其材料参数如表1所示．硬化段采用库伦-摩尔模型．

2.2.2 计算结果与分析

图6为渗流、砂土硬化和软化条件下，不同支护力比的开挖面中心点位移．支护力比是盾构界面支护力与盾构界面处土体静止侧向上压力的比值．

图6 支护力比和开挖面中心点的水平位移关系曲线Fig.6 Relationship between support pressure ratio and horizontal displacement of face

从图中可以看出，当支护力比大于0.6时，砂土的掘进面的开挖面中心点位移基本相同，当支护力比小于0.6后，两者的差别越来越大，这时砂土软化带来的影响愈来愈显著．考虑砂土软化的掘进面的临界支护力比，比硬化情况下要小，前者为0.5，后者为0.525．可见土体在软化条件下极限支护力降低．支护力比同为0.5时两者的塑性区发展如图7所示．

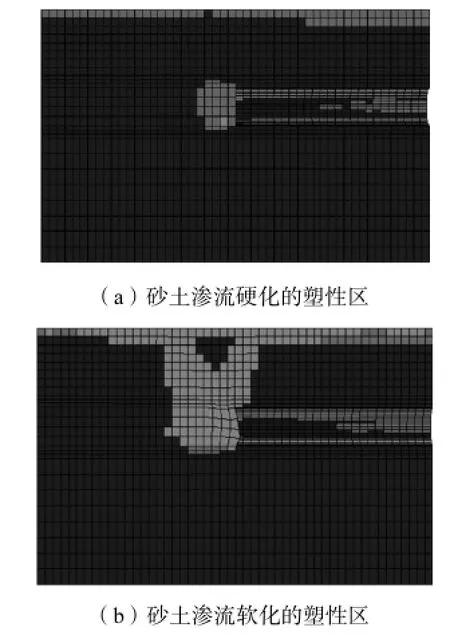
图7 塑性区发展云图Fig.7 Nephogram of plastic zone

从图7可以看出，没有应变软化的土体中塑性区虽然得以扩展，但扩展范围较小，还没有和地面贯通．但在软化的土体中，塑性区已大范围扩展，并与地面贯通，地表沉降很大，掘进面前方已形成楔形体，开挖面失稳，两者的差别是很明显的．

3 土体应变软化参数变化的影响

软件中的应变软化模型是通过定义软化参数的分段线性函数来实现．对内摩擦角、黏聚力2个软化参数，在只改变其中一个参数的情况下，比较分析不同参数时的极限支护力比、塑性区扩展等来说明这2个参数对盾构掘进界面稳定性的影响．

3.1 内摩擦角对应变软化的影响分析

3.1.1 计算模型、材料参数及方案选择

计算模型、材料参数除内摩擦角外与图5完全一致，共取3种方案，每个方案下的内摩擦角取值如图8所示．

图8 3种方案的内摩擦角Fig.8 Friction angles of three programs

3.1.2 数值计算结果分析

图9所示为方案1至方案3下的支护力比和开挖面水平位移关系曲线，从图中可以得出每个方案的极限支护力，见表2．

图9 不同内摩擦角下支护力比和开挖面水平位移关系曲线Fig.9 Relationship between support pressure ratio and horizontal displacement of face under different friction

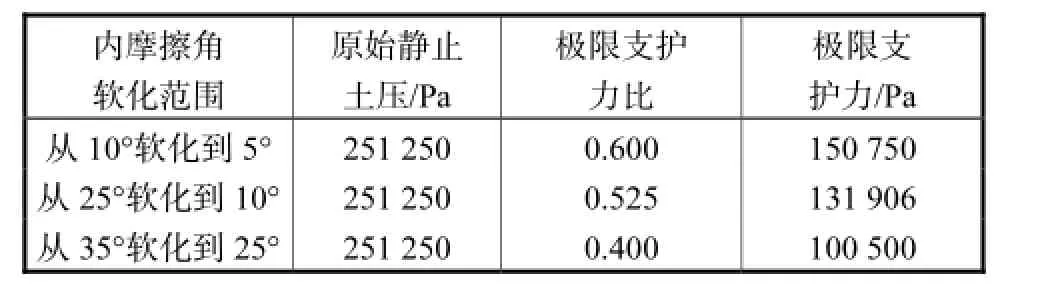
表2 不同内摩擦角软化下开挖面极限支护力Tab.2 Limit support pressure under different internal friction angle

从图9中可以看出内摩擦角取值不同时极限支护力比相差较大，说明内摩擦角对应变软化的影响非常明显．

为了进一步说明摩擦角对软化条件下的开挖面稳定性影响，这里取各个方案下支护力比为0.525时的塑性区扩展图进行比较，如图10所示．

图10 内摩擦角软化塑性区发展云图Fig.10 Nephogram of plastic zone for internal friction angle softening

3.2 黏聚力对应变软化的影响分析

3.2.1 计算模型、材料参数及方案选择

计算模型、材料参数除黏聚力外都与图5完全一致，共取3个方案，3个方案下的黏聚力取值见图11所示．

3.2.2 数值计算结果分析

图12所示为3个方案下的支护力比和开挖面水平位移关系曲线，从图中可以得出每个方案的极限支护力，见表3．

图12 不同黏聚力下支护力比和开挖面水平位移关系曲线Fig.12 Relationship between support pressure ratio and horizontal displacement of face under different cohesion

表3 不同黏聚力软化下开挖面极限支护力Tab.3 Limit support pressure under different cohesion

图13为支护力比为0.475时模型的塑性区发展图，在黏聚力3,kPa软化到2,kPa时，塑性区完全扩充到地表；当黏聚力从6,kPa软化到4,kPa时，塑性区刚刚发展为楔形体状，且没有扩展到地表；当黏聚力10,kPa软化到7,kPa时，塑性区很小．

图13 黏聚力软化塑形区发展云图Fig.13 Nephogram of plastic zone for cohesion-softening

通过对应变软化参数内摩擦角和黏聚力进行对比分析，可以看出内摩擦角对应变软化产生的影响较大，黏聚力次之．

4 工程实例分析

4.1 工程概况

天津地铁9号线十一经路站到大直沽西路站区间，隧道内径为6.32,m，采用小松公司的TM634PMX 土压平衡盾构机．隧道衬砌采用35,cm厚的C50混凝土管片，管片环宽1.2,m，总共掘进1,000多环，其中300～400环区间隧道埋深相差不大，平均埋深14.3,m．考虑到地层条件的复杂及开挖面位置土层的不确定性，对分析底层进行简化，地下水位距地表1,m．

4.2 计算模型

为解决FLAC3D软件建模的不足，利用其系统的开放性，通过专业建模工具AutoCAD精确建立三维模型，然后将模型导入ANSYS，利用其强大的网格划分功能对模型进行网格划分；最后通过转换程序将数据转化成FLAC3D的数据，即实现模型的导入．通过此方法实现在 FLAC3D软件中快速建立复杂三维地质模型(见图14)．在建模过程中，考虑简化模拟计算需要，将地质情况进行了以下简化：①同类相接地层合并；②地层尖角简化成方角；③隧道水平绘制，埋深取平均值．

4.3 数值计算

分析开挖30,m、50,m和90,m时的地表沉降，开挖50,m时的计算模型尺寸如图14所示．边界条件为：模型侧面和底面为位移边界，侧面限制水平位移；底部为固定边界，限制水平移动和垂直位移；模型上面为地表面，为自由边界．

图14 计算模型Fig.14 Numerical calculation model

在盾构推进过程中，由于土体的开挖，改变了天然土体的原始平衡状态．掘进面支护力的大小与掘进面前方地表沉降密切相关．

在地铁隧道施工中，隧道要穿越城市中心地带，地面建筑物密集、地下管网密布，因而对地表的控制要求较为严格．要求盾构掘进时开挖面前方地表沉降不超过3,mm，以及隆起量控制在2～3,mm．根据计算得到的盾构掘进时地表的隆降曲线可以得出掘进面合理支护力比范围，开挖30,m时为0.4～1.4，开挖50,m时为0.5～1.5，开挖90,m时为0.4～1.5，而开挖面土层原始侧向土压力为0.27,MPa，所以，预测的合理的支护压力范围则是开挖30,m时为0.108～0.378,MPa，开挖50,m时为0.135～0.405,MPa，开挖90,m时为0.108,MPa～0.405,MPa．图15为数值计算结果与工程实测数据的对比分析．

图15 土压监测值Fig.15 Monitoring values of soil pressure

实测支护力数据都是在土体掘进过程中瞬时测得的，数值是瞬态的，虽然有的实测瞬态峰值超出了模拟的上下极限值，但由于这种超出只是瞬时的、短暂的，并很快回落到模拟的上下限范围之内，所以塑性区来不及扩展，掘进面依然是安全的．如果极限支护力长时间处于实测曲线中的峰值状态，则掘进面就会失稳．

从图中还可以看到，工程中测得的绝大部分支护力数据都落在本文预测的上下限支护力范围之内．

5 结 论

(1) 数值模拟得到的砂土中的剪切带与实验结果基本吻合，在峰值状态附近出现应变局部化现象，峰值过后应变局部化继续扩展．

(2) 砂土应变局部化的扩展对盾构掘进面的稳定性影响很大．应变软化的土体其极限支护力要大于应变硬化的土体，塑形区扩展也较大．因此，对于应变软化岩土材料，忽略其软化的行为是偏于危险的．

(3) 土质应变软化参数的分析中，内摩擦角影响最大，黏聚力次之．

(4) 以天津地铁9号线为工程实例，考虑渗流及土体应变软化时，根据开挖面前方地表的变形情况,对合理的支护力范围进行预测，得到的范围与实际监测的土仓压力波动范围基本一致．

［1］ 孙 均. 城市地下工程活动的环境土工学问题(上)[J]. 地下工程与隧道，1999，13(3)：2-6.

Sun Jun. Research on environmental soil engineering works during underground construction activities in urban area(Ⅰ)[J]. Underground Engineering and Tunnels，1999，13(3)：2-6(in Chinese).

［2］ 孙 均. 城市地下工程活动的环境土工学问题(中)[J]. 地下工程与隧道，1999，13(4)：7-9.

Sun Jun. Research on environmental soil engineering works during underground construction activities in urban area(Ⅱ)[J]. Underground Engineering and Tunnels，1999，13(4)：7-9(in Chinese).

［3］ Leca E，Dormieux L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J]. Geotechnique，1990，40(4)：581-606.

［4］ 李林福，彭芳乐. 平面应变条件下砂土局部化剪切带的有限元模拟[J]. 岩石力学与工程学报，2010，29(4)：850-857.

Li Linfu，Peng Fangle. Finite element simulation of strain localization on a shear band of sand under plane strain condition[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(4)：850-857(in Chinese).

［5］ 赵启林，牛海清，卓家寿. 应变软化材料的几个基本问题研究进展[J]. 水利水运工程学报，2001，23(3)：73-77.

Zhao Qilin，Niu Haiqing，Zhuo Jiashou. Basic problems of strain-softening material[J]. Hydro-Science and Engineering，2001，23(3)：73-77(in Chinese).

［6］

Zheng H，Liu D F，Lee C F，et al. Principle of analysis of brittle-plastic rock mass[J]. International Journal of Solids and Structures，2005，42(1)：139-158.

［7］ 周家文，徐卫亚，李明卫，等. 岩石应变软化模型在深埋隧洞数值分析中的应用[J]. 岩石力学与工程学报，2009，28(6)：1116-1127.

Zhou Jiawen，Xu Weiya，Li Mingwei，et al. Application of rock strain softening model to numerical analysis of deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering，2009，28(6)：1116-1127(in Chinese).

［8］ 王学滨. 材料缺陷对岩样变形局部化影响的数值模拟[J]. 岩土力学，2006，27(8)：1241-1247.

Wang Xuebin. Numerical simulation of influence of material imperfection on strain localization[J]. Rock and Soil Mechanics，2006，27(8)：1241-1247(in Chinese).

［9］ Brown E T，BrayJ W，Ladanyi B，et al. Ground response curves for rock tunnels[J]. Journal of Geotechnical Engineering，1983，109(1)：15-39.

［10］ Alonso E，Alejano L R，Varas F，et al. Ground response curves for rock masses exhibiting strain-softening behavior[J]. International Journal for Numerical and Analytical Menthods in Geomechanics，2003，27(6)：1153-1185.

［11］ Alshibli K A，Sture S. Shear band formation in plane strain experiments of sand[J]. Journal of Geotechnical and Geoenvironmental Engineering，2000，126(6)：495-503.

［12］ Desrues J，Viggiani G. Strain localization in sand：An overview of the experimental results obtained in Grenoble using stereophotogrammetry[J]. Int J Numer Anal Meth Geomech，2004，28(2)：279-321.

［13］ Zhang Y T，Qi D X，Gao J，et al. Analysis of kinking in elastoplastic materials with strain-softening behavior[J]. Inter J Eng Sci，2008(46)：1077-1086.

［14］ Papamichos E，Vardoulakis I. Shear band formation in sand according to non-coaxial plasticity model[J]. Geotechnique，1995，45(4)：649-661.

［15］ Vardoulakis I. Deformation of water-saturated sand：In uniform undrained deformation and shear banding[J]. Geotechnique，1996，46(3)：441-456.

［16］ 宁加星. 砂土应变局部化的数值分析[D]. 天津：天津大学机械工程学院，2010.

Ning Jiaxing. The Numerical Analysis of Strain Localization in Soil[D]. Tianjin：School of Mechanical Engineering，Tianjin University，2010(in Chinese).

Analysis on Stability of Shield Tunneling Face in Soil with Strain-Softening Behavior

Zhang Yitong1，Zhu Long1，Ning Jiaxing2
(1. School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Metro Group Company Limited，Tianjin 300240，China)

Many kinds of soil in geotechnical engineering display strain-softening behavior ,which can result in strain localization and, furthermore, the instability of soil. On the basis of the local strain fields in the specimen obtained from the drained plane strain compression test on saturated sand, the paper first makes a numerical analysis to predict the experimental phenomenon. Then, the strain-softening influence of shield excavation surface instability is considered, three-dimensional numerical simulation for deep shield tunneling is performed, and the strain hardening and softening models in the condition of seepage are compared, so are the seepage and non-seepage models in the condition of strain softening. The analysis shows that, compared with soil without strain-softening behavior, the strain-softening of soil more easily causes the instability of shield tunneling face, increases the limits of face pressure and the settlement of the ground, and leads to more expansion of plastic regime. How the change of the values of strain-softening parameters, such as internal friction angle and cohesion, affects the instability of shield tunneling face is discussed, and it is found that internal friction angle has a great influence, followed by cohesion. Finally, the shield tunneling in a section of Tianjin Metro Line 9 is simulated, and the results are consistent with the measured data.

sand；strain-softening；strain localization；shear band；shield；instability of tunneling face

U455.43

A

0493-2137(2013)07-0596-07

DOI 10.11784/tdxb20130705

2011-03-09；

2011-09-12.

国家重点基础研究发展计划(973计划)资助项目(2013CB035402).

张义同（1945— ），男，教授.

张义同，ytzhang@tju.edu.cn．