复数三阶累积量在液压阀故障诊断中的应用

吴文兵，杨淑群，周桃庚

(1. 厦门大学信息科技学院，厦门 361000；2. 福州外语外贸学院公共教学部，福州 350201；3. 福建师范大学软件学院，福州 350007；4. 北京理工大学光电学院 北京 100081)

复数三阶累积量在液压阀故障诊断中的应用

吴文兵1,2，杨淑群3，周桃庚4

(1. 厦门大学信息科技学院，厦门 361000；2. 福州外语外贸学院公共教学部，福州 350201；3. 福建师范大学软件学院，福州 350007；4. 北京理工大学光电学院 北京 100081)

为了提高故障诊断正确率，提出了一种基于复数三阶累积量的机械故障诊断方法．三阶累积量的不同定义的复数形式包含了信号间不同的耦合信息，利用这些信息进行了故障诊断．在溢流阀故障诊断实验中,利用这些不同的耦合信息，通过二维小波在不同的方向上对故障信号和正常信号进行特征提取，然后将这些特征值输入支持向量机进行故障判别．实验结果表明，上述方法可以提高故障诊断正确率．同时还对实数三阶累积量也进行了相同的实验，这些实验所取得的诊断效果证明了采用本文方法的有效性．

三阶累积量；耦合；溢流阀；故障诊断

高阶累积量可以自动地抑制高斯背景噪声(有色或白色)的影响，建立高斯噪声下的非高斯信号模型，提取高斯噪声中的非高斯信号(包括谐波信号)[1]．正因为这样，高阶累积量这一统计量已日益受到人们的重视并已成为信号处理中一种非常有用的工具．由三阶累积量得出的双谱包含了信号的非对称、非线性信息，可以用来描述非线性相位耦合，尤其是二次相位耦合，已经在故障诊断中得到了广泛应用[2-4]．

Stronach和Kocur等[5-6]对高阶谱进行了深入研究，并将其应用到各种机械故障诊断中；Raughveer和国内学者王树勋等[7-9]对高阶累积量的耦合性质进行了深入研究，明确指出了各种复数高阶累积量的不同定义形式的耦合特征．小波分析以其良好的时频特性，成为信号分析的有力工具，特别在对非线性、非平稳信号的分析时优点更为明显．与傅里叶变换相比，小波分析能够在足够的时间分辨率的前提下，对信号的短时高频成分进行分析，又能在很好的频率分辨率下，对信号的低频进行估计．人工神经网络是一个自适应非线性动态信息处理系统，可以通过样本学习训练改变网络权值，使实际输出和期望输出满足规定的误差要求．因此，神经网络模型可以作为故障分类器进行故障诊断．

由于实际的机械振动信号具有非线性、非平稳的特点，而小波变换能有效地处理这类信号，因此笔者根据溢流阀振动信号的不同耦合特性，利用二维小波进行特征提取，再将提取的特征值输入最小二乘支持向量机(least square support vector machine，LSSVM)进行故障诊断．

1 基于复数三阶累积量的故障诊断方法

1.1 三阶累积量耦合性质

令{x(n)}为零均值k阶平稳随机过程，则其三阶累积量为

根据文献[10]，令x(n)为复数信号，并进行如下定义．

定义1

定义2

定义3

式中()x n∗为x(n)的共轭复数，本文的复数信号由采集的原始信号进行Hilbert变换得到．文献[10]指出，按定义1的方式，可以用复数谐波形式表示的发生了2次相位耦合的信号其三阶累积量为0，以定义2的方式其三阶累积量仅包含参加耦合的谐波信号，而按定义3的方式其三阶累积量则既包含参加耦合的谐波信号，也包含耦合后的信号．

1.2 二维小波多尺度分解

二维小波函数是通过一维小波函数经过张量积变换得到的，二维小波函数分解是把尺度j的低频部分分解成4部分：尺度j+1的低频部分和3个方向(水平、垂直、斜线)的高频部分．

设原始二维数组共有N×N个元素，尺度参数j= 0，由原始二维数组开始进行递推分解，在第j级分解，小波系数矩阵降低到(2j-N)2个元素(分辨率降低了2j-)，由于因子j既表示分解级数，又与二维数组的分辨率相关，因此常将j称作分辨率或分解尺度[10-11]．

1.3 数据采集

当内部主阀弹簧损坏，阻尼孔受阻，先导阀弹簧损坏，或进油口有异物、出现漏油现象，都会使得溢流阀产生故障，无法正常起作用．为了获取溢流阀在故障状态下的运行信号，本文进行的实验人为设置了如下故障，即使先导阀弹簧变形．通过实验可以近似模拟溢流阀工作故障状况．

本文利用LabVIEW软件及PCI-6,014的数据采集卡和一个加速度传感器，依次采集减压阀在正常和故障状态下的振动信号．在每种测量中，将油路压力从1～5,MPa分5个压力等级．采样频率250,Hz，读取频率125,Hz，采样过程时间约2,min．本次实验在溢流阀正常工作状态和故障状态分别采集了18组共36组数据．本文实验使用的数据个数为1,536个.

1.4 复数三阶累积量

本实验首先将正常状态和故障状态的36组数据，按前述3种定义方式得出每组数据的三阶累积量．本文选取正常状态和故障状态数据的复数三阶累积量进行图示，令-127≤(12,τ τ)≤127，再在油压分别为1,MPa、2,MPa和4,MPa时，在定义3方式下，将2种状态的三阶累积量取绝对值后各选取1组，见图1和图2．图中x、y轴表示滞后量，纵轴表示归一化后的幅值大小，均无量纲．由图1和图2可以看出，故障状态的三阶累积量与正常状态相比，其峰值分布更稀疏些．

1.5 特征提取

本文在故障识别时，如果直接采用将所获得的三阶累积量数据输入神经网络，一是运算量太大，二是通过实验所获得的诊断结果也不理想．由于原始信号中所包含的各种频率信息必然反映到其三阶累积量中，而小波分解又能有效提取这些频率信息，故本文采用二维小波分解对测量到的每组数据的不同耦合方式的三阶累积量进行特征提取，本文使用的是db1小波[8-9]．通过实验对比分析，在对原始数据进行二维小波函数分解后，并提取尺度为6时的6级压缩系数作为LSSVM输入向量时取得了最佳识别效果，压缩后的系数为4×4的二维数组．本文在低频部分和3个方向(水平、垂直、斜线)的高频部分分别进行了特征提取，图3和图4中表示的是按斜线的高频部分压缩并取模后的特征值，其中x、y轴分别表示压缩后的二维矩阵的维数，z轴表示提取归一化后的特征值，均无量纲．表1给出了在定义3方式下，正常状态和故障状态各3组数据按照高频斜线方向进行压缩所获得的特征向量．

图1 定义3方式下正常下状态复数三阶累积量Fig.1 Complex three-order cumulants of definition 3 in normal state

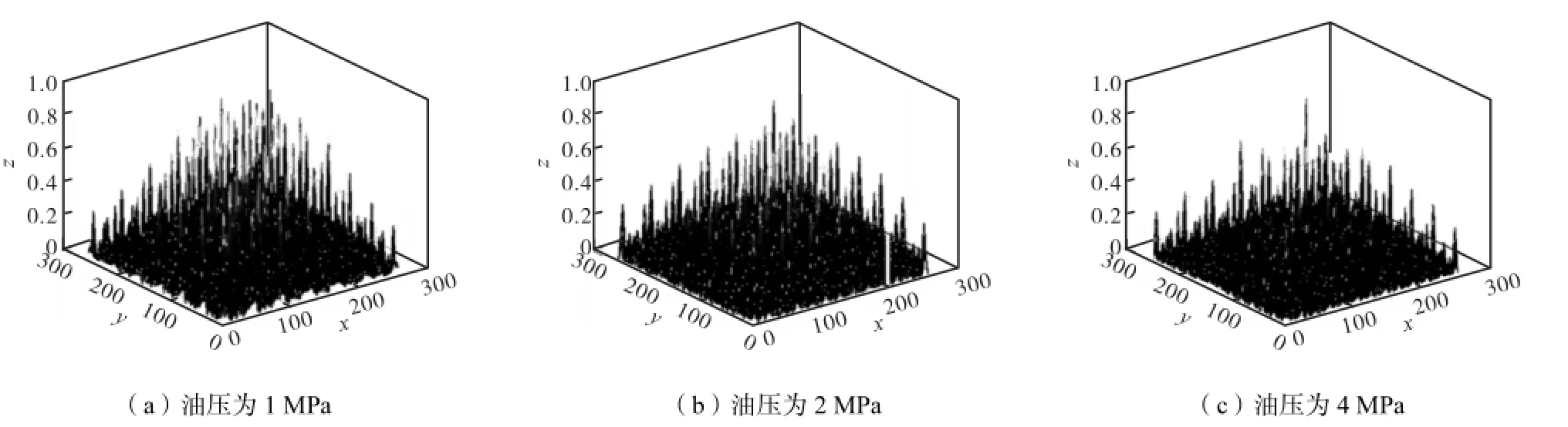
图2 定义3方式下故障状态复数三阶累积量Fig.2 Complex three-order cumulants of definition 3 in fault state

图3 定义3方式下正常状态复数三阶累积量按斜线方向提取特征值Fig.3 Diagonal wavelet coefficients of complex three-order cumulants of definition 3 in normal state

图4 定义3方式下故障状态复数三阶累积量按斜线方向提取特征值Fig.4 Diagonal wavelet coefficients of complex three-order cumulants of definition 3 in fault state

表1 定义3方式下复数三阶累积量按斜线方向提取的特征值Tab.1 Complex three-order cumulants’ features extracted in diagonal direction of definition 3

2 实验结果

机械故障诊断包括信号获取、信号处理和故障模式分类3个环节，其中故障模式分类是诊断的核心内容．支持向量机(support vector machine，SVM)是为解决二类分类问题而提出，并迅速发展成为一种分类问题的有力工具，已成功地应用于许多工程领域，如语音识别、图像分类等．LSSVM是基于SVM方法的一种改进算法．LSSVM方法采用最小二乘线性系统作为损失函数，与经典SVM不同，它只有等式约束，而无不等式约束，加快了计算的速度．本文根据文献[12]，建立了相同的LSSVM．在训练LSSVM时，分别将正常状态和故障状态编码为1和-1，由于正常数据和故障数据分别是在5种不同的油压下获得的，训练时分别在表1的正常数据和故障数据中取出相对应的5组数据共10组，对所建立的最小二乘支持向量机进行训练，训练结束后再利用该支持向量机进行故障识别，利用训练后的网络对所剩下的26组数据进行模拟识别，如图5所示，其中图例的含义与文献[12]相同．图5显示，在定义3方式下，按照斜线的高频部分所获得的特征向量进行识别，正常状态和故障状态各有2组、共4组识别错误，正确率达到80%以上．为了便于对比，将按3种不同的定义方式、4个不同方向进行特征提取后所得到的模拟结果列于表2，表2中的数字表示模拟识别时的错误数．为了进行进一步的分析，将实数三阶累积量也进行上述相同的实验，结果见表2．同时按照前述方式，在油压分别为1,MPa、2,MPa和4,MPa时，将2种状态的实数三阶累积量取绝对值后各选取1组示于图6和图7，其量纲与图1和图2类同．由图6和图7可以看出，与复数三阶累积量相比，实数三阶累积量的故障状态图与正常状态图之间，在谱峰分布的疏密程度上要更为相似些．

图5 定义3方式下按斜线方向特征提取故障诊断模拟结果Fig.5 Simulating result of fault diagnosis in diagonal direction of definition 3

表2 各种定义方式下模拟结果错误数Tab.2 Simulating error numbers in all kinds of definition

图6 正常状态实数三阶累积量Fig.6 Real three-order cumulants in normal state

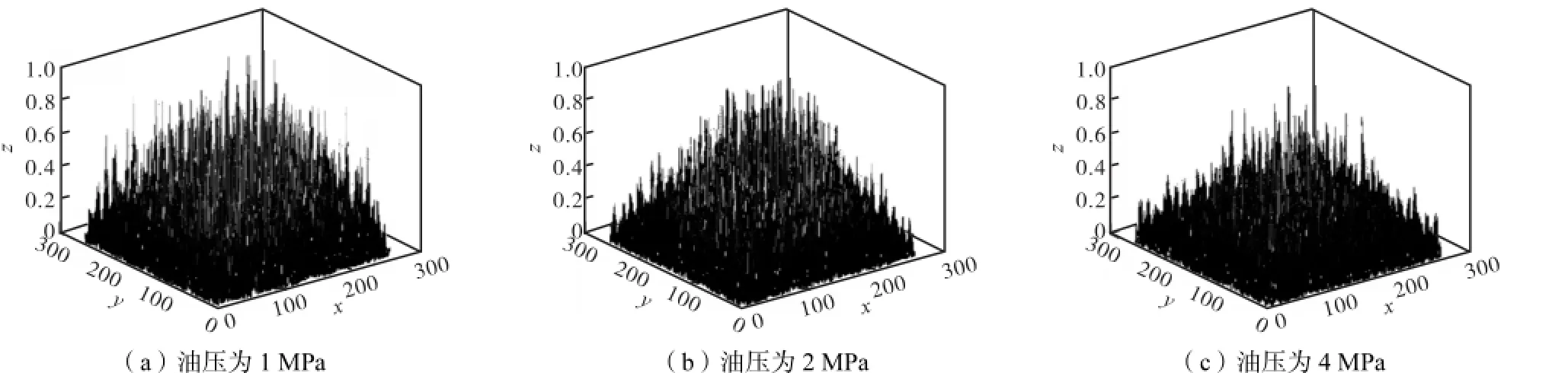
图7 故障状态实数三阶累积量Fig.7 Real three-order cumulants in fault state

3 实验结果分析

如前所述，高阶累积量可以自动地抑制高斯背景噪声(有色或白色)的影响，二维小波函数分解可以把尺度j的低频部分分解成4部分．本文采用二维小波的方法，在3种不同的耦合方式下，同时对正常信号和故障信号在低频部分和3个方向(水平、垂直、斜线)的高频部分进行了特征提取，并利用提取的这些信息进行故障诊断，结果表明，由于三阶累积量在不同的耦合方式下，包含了不同的频率信息，同时又在4个不同方向进行特征提取，利用提取的这些不同的频率信息进行故障诊断时，所得到的正确率也不一样．本文的实验结果表明，3种定义方式在不同的特征值提取方向上，所得到的诊断效果各有优劣，但在定义3方式下，即当复数三阶累积量中既包含了参加耦合的信号信息、也包含了耦合后的信号信息，并按照高频部分的斜线方向进行特征提取时，所得到的故障诊断效果最佳．同时为了证明采用本文方法的必要性，令-1≤(12,τ τ)≤2，再按式(6)求出采集的每组数据相应的三阶累积量，也是16维数组，与前述的二维小波压缩后的数据个数相同，并将这些数据作为特征值，按前述方法进行故障诊断，所得结果如图8所示，从图中可以看到，结果是很不理想的，因此，本文首先通过令-127≤(12,τ τ)≤127得出三阶累积量，再利用二维小波压缩进行特征提取，比直接计算相同个数的三阶累积量进行故障诊断，其效果是要更好的，也说明三阶累积量中1τ、2τ滞后量过小时所包含的信号信息是不完整的，随着1τ、2τ逐渐增大，诊断效果也逐渐变好，当1τ、2τ在80左右时，诊断效果渐趋稳定．而本文通过计算较大滞后量，再通过小波进行特征提取的方法所获得的数据，则包含了较为完整的信号信息，从而取得了较为满意的故障诊断效果．实验最后还用同组数据的AR参数按照文献[12]、AR功率谱和实数双谱对角切片按照文献[13]的方法进行了故障诊断，其正确率均在70%以下，这也进一步说明了本文方法的有效性．

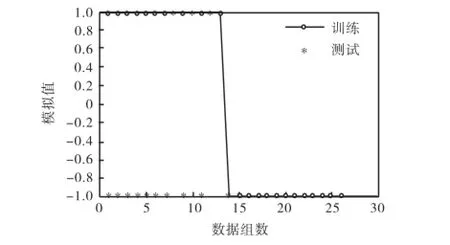
图8 定义3方式下16维三阶累积量值作为特征值向量的故障诊断模拟结果Fig.8Simulating result of fault diagnosis of definition 3 when three-order cumulants with 16-D used as features vectors

4 结 语

尽管各种机械故障产生的机制不一样，但每种故障均存在和正常状态最本质的区别，如本文中的故障就是因为在正常状态的溢流阀弹簧变形而引起的，这种本质上的区别就使得故障状态下的信号与正常状态下的信号相比，有可能在某种信号特征上两者区别最大．本文通过复数三阶累积量的不同定义方式，二维小波在不同的方向上提取特征值寻找最佳诊断效果，取得了一定程度的成功．

［1］ 张贤达. 现代信号处理[M]. 北京：清华大学出版社，2002. Zhang Xianda. Modern Signal Processing[M]. Beijing：Tsinghua University Press，2002(in Chinese)．

［2］ 蔡奇志，黄宜坚. 自回归三谱切片研究[J]. 仪器仪表学报，2009，30(2)：345-350.

Cai Qizhi，Huang Yijian. Study on autoregressive trispectrum slices[J]. Chinese Jouma1 of Scientific Instrument，2009，30(2)：345-350(in Chinese)．

［3］ 邵忍平，黄欣娜，刘宏昱. 基于高阶累积量的齿轮系统故障检测与诊断[J]. 机械工程学报，2008，44(6)：161-168.

Shao Renping，Huang Xinna，Liu Hongyu. Fault detection and diagnosis of gear system based on higher order cumulants[J]. Journal of Mechanical Engineering，2008，44(6)：161-168(in Chinese)．

［4］ 段向阳，王永生，苏永生. 切片双谱分析在离心泵故障诊断中的应用[J]. 振动、测试与诊断，2010，30 (5)：581-584．

Duan Xiangyang，Wang Yongsheng，Su Yongsheng. Application of slice bispectrum analysis to fault diagnosis[J]. Journal of Vibration，Measurement & Diagnosis，2010，30(5)：581-584(in Chinese)．

［5］ Yang D M，Stronach A F，Macconnell P，et al. Thirdorder spectral techniques for the diagnosis of motor bearing condition using artificial neural networks[J]. Mechanical Systems and Signal Processing，2002，16(2/3)：391-411.

［6］ Kocur D，Stanko R. Order bispectrum：A new tool for reciprocated machine condition monitoring[J]. Mechanical Systems and Signal Processing，2000，14(6)：871-890.

［7］ Raughveer M R. Time-domain approaches to quadratic phase coupling estimation[J]. IEEE Trans on Automatic Control，1990，35(1)：48-56．

［8］ 张 严，王树勋. 非线性相位耦合的切片谱分析方法[J]. 电子学报，1998，26(10)：104-109.

Zhang Yan，Wang Shuxun. The slice spectra approach to nonlinear phase coupling analysis[J]. Acta Electronic Sinica，1998，26(10)：104-109(in Chinese).

［9］ 李允公，刘 杰，朱启兵，等. 基于复值过程高阶累积量谱的轴心轨迹分析的研究[J]. 机械工程学报，2005，41(1)：157-161.

Li Yungong，Liu Jie，Zhu Qibing，et al. Study of orbit analysis based on complex process high order cumulant spectrum[J]. Journal of Mechanical Engineering，2005，41(1)：157-161(in Chinese)．

［10］ 吴文兵，黄宜坚，陈文芗. 复双谱耦合性质在故障诊断中的应用[J]. 北京工业大学学报，2012，38(9)：1287-1292.

Wu Wenbing，Huang Yijian，Chen Wenxiang. Application of complex bispectral coupling properties in fault diagnosis[J]. Journal of Beijing University of Technology，2012，38(9)：1287-1292(in Chinese)．

［11］ 宫伟力，李 晨. 煤岩结构多尺度各向异性特征的SEM图像分析[J]. 岩土力学与工程学报，2010，29(增1)：2681-2689．

Gong Weili，Li Chen. Multi-scale and anisotropic characterization of coal structure based on sem image analysis[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(Suppl 1)：2681-2689(in Chinese).

［12］ 吴文兵，黄宜坚. 基于双相干谱的减压阀故障诊断[J]. 计算机测量与控制，2011，19(10)：2413-2416.

Wu Wenbing，Huang Yijian. Fault diagnosis of reducing valve based on bispectra slices[J]. Computer Measurement and Control，2011，19(10)：2413-2416(in Chinese).

［13］ 吴文兵，黄宜坚. 功率谱在调速阀故障诊断中的性能分析[J]. 制造技术与机床，2011(12)：198-201.

Wu Wenbing，Huang Yijian. The performance analysis of power spectrum in a regulating valve′s fault diagnosis[J]. Manufacturing Technology and Machine Tool，2011(12)：198-201(in Chinese).

Application of Complex Three-Order Cumulants to Fault Diagnosis of Hydraulic Valve

Wu Wenbing1,2，Yang Shuqun3，Zhou Taogeng4
(1. School of Information Science and Engineering，Xiamen University，Xiamen 361000，China；2. Department of Basic Courses，Fuzhou College of Foreign Studies and Trade，Fuzhou 350201，China；3. Faculty of Software，Fujian Normal University，Fuzhou 350007，China；4. School of Optoelectronics，Beijing Institute of Technology，Beijing 100081，China)

In order to improve the correction rate of fault diagnosis, one method of mechanical fault diagnosis based on complex three-order cumulants was proposed. The complex forms with different definitions of three-order cumulants included different coupling information of signals，which was used to diagnose fault. In the experiment on the fault diagnosis of overflow valve，using the different coupling information, the features of fault signals and normal signals were extracted by 2-D wavelet in different directions，and then they were input into support vector machine to diagnose the fault. The experiment results show that this method can improve the correction rate of diagnosis. Furthermore，the same experiment was performed on the real three-order cumulants，and the results verify the effectiveness of the method proposed in this paper.

three-order cumulants；coupling；overflow valve；fault diagnosis

TG156

A

0493-2137(2013)07-0590-06

DOI 10.11784/tdxb20130704

2012-02-02；

2012-06-03.

国家自然科学基金资助项目(50975098)．

吴文兵（1968— ），男，博士，副教授，wwbysq@fjnu.edu.cn．

周桃庚，bitzhtg@bit.edu.cn.