基于QUAKE/W均质土坝地震响应静力学分析计算
2021-01-06程琦
程 琦
(塔城地区水利水电勘察设计院,新疆 塔城 834700)
0 引 言
土石坝的抗震分析与计算,其目的在于通过使用各种可靠的计算方法,来得出土石坝在其设计地震动力作用的情况下,所发生的各种大坝动力响应,如坝体的位移变形、动应力、动应变和加速度等;并能够预测大坝可能产生的种种形式的破坏,如坝基失稳、裂缝、滑坡、渗漏、滑裂以及沉降等,从而来改进工程设计的缺陷,采取相应的地震加固措施,用以保证该土石坝的抗震稳定[1-3]。就目前来说,土石坝的抗震稳定性研究工作主要集中在大坝的动力分析、稳定性分析、坝基和坝体的液化分析和整体稳定性分析以及坝体永久变形等计算方面,但对于坝体渗漏或是裂缝等地震破坏形式目前仍缺乏相对可靠的计算分析方法[4]。
静力场分析程序基于有限元技术,可以计算坝体-坝基体系在自重、渗透力和其它外荷载约束下每一单元的初始应力分量[5]。同时,该程序可以模拟坝体施工过程和水库蓄水过程,进行分级加载,以便合理地计算坝体-坝基体系内各点的应力情况。程序中,采用邓肯-张模型来考虑静力非线性特性[6]。
1 工程概况
某水库位于Y市西北部的Z县,该水库大坝为均质土坝,坝型比较具有一般性。该水库以灌溉农田为主,大坝为均质土坝,坝轴线呈南北方向,两岸坡较陡,坝高52 m,坝顶宽6 m,长272 m,迎水坡坡比为1∶2.75,背水坡坡比为1∶2.5,背水坡设有宽2.5 m的马道,高为10 m的排水棱体,大坝坝顶高程1 369.00 m,正常蓄水位1 366.00 m。
2 静力学计算参数
本次计算围绕以下两种计算工况展开,即竣工期和稳定渗流期。其中,竣工期工况为坝前坝后均无水的情况;稳定渗流期工况是上游为正常蓄水位、下游为相应水位时坝坡的稳定情况。模型划分为330个单元与460个节点。坝体与地基横断面的单元剖分图见图1。

图1 模型单元剖分图
其中,对于该坝体静力计算参数的邓肯-张参数见表1。

表1 模型参数表
3 计算结果
3.1 计算原理
为了了解坝体的渗透力、自重,对土石坝的静力进行有限元深入分析,并对其余坝体-坝基(载荷作用)的静应力的分布情况进行研究。检验一个土石坝静力稳定与否,只需要检查坝体-坝基中单元应力的分布状况,即提供动力分析的初始条件,从而确定坝体内部各单元初始的静围压。静应力在地震发生作用下的强度特性和变形特性均影响较深,是在地震之前土单元所受到的初始应力。土体本构用的是非线性的静力本构关系,目的是提升静力的计算精度。邓肯-张模型可以很好的说明正常固结的黏性土、中密砂以及松砂的应变应力关系。此外,在土坝的静力有限元的分析中,通常采用是邓肯-张模型其中静力非线性本构关系邓肯-张模型,由邓肯-张模型应力应变关系,可以得到土切线量Es的表达式为[7]:
(1)
3.2 静力学分析结果
土石坝在水库的水压力和自身重力的作用下将会产生很多形变,其中水平横向位移(坝轴线垂直方向)、竖直位移(沉降)和水平纵向位移(坝轴线平行)的一部分(竖直位移)会从施工期中产生,另外一部分由运行期产生。若形变数值不是很大,坝体正常的运用不受影响,但是如果形变到一定程度,就会影响坝体的安全运用,如沉降过大会降低坝体高度,从而造成洪水来袭时坝体顶端漫溢;不均匀的水平位移和沉降会使坝体破坏和产生裂缝。位移符号通常是单位为m,水平位移时上游方向是正,竖向位移时向上是正。
坝体竣工期土自重是竣工期引起坝体形变和应力的主要因素。坝体在自身重力荷载时会产生水平位移和垂直沉降。坝体最大数值沉降为0.91 m,大约是坝体高度的1.77%,一般在坝顶端的中间部位出现。当方向指向上游时,上游坝体的水平位移最大是0.475 m;当方向指向下游时,下游坝体的水平位移最大是0.257 cm,上下游水平位移的最大值主要出现在上下游坝体坡面接近坝体基底部的附近,在上下游大约1/4坝体高度处。水平位移的等值线一般沿着坝体轴线两侧,并且对称分布。竣工期坝体的X、Y向位移计算结果见图2和图3。

图2 竣工期坝体的X向位移图
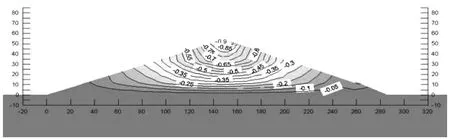
图3 竣工期坝体的Y向位移图
引起大坝在蓄水期形变的主要因素有:浸水以后坝体内部所形成的湿化变形,作用在坝体的上下游水压力以及水对于上游坝体面的浮托力。蓄水之后在上游的水压力和自重荷载的共同作用下,坝体会产生水平位移和垂直沉降。坝体最大的垂直沉降等值线的分布规律和竣工时比较接近。蓄水以后,上游的坝面在正常蓄水位之下时,容重就会变成浮容重,而且会受到浮托力的影响,上游那面的坝体会有向上抬起的趋势;相同地,水压力作用在坝体内部,使得下游侧的坝体会有向坝基、向下游滑动的趋势,导致上游侧的坝体产生同等的位移变化趋势。总的来说,蓄水之后的大坝垂直方向位移会较竣工期有所增大,最大的沉降变形值是1.45 cm,一般在坝体顶端的中部出现,约是坝体高度的1/10处。因为受到上游的坡面水压力作用,水平位移有朝着坝体下游滑动的倾向,最大值一般在下游的坝坡处。其他值从0.475 cm(指向下游方向)变成0.515 cm(指向下游方向),一般在坝体下游接近排水棱处出现。见图4和图5。

图4 稳定渗流期坝体X向位移图(单位:m)
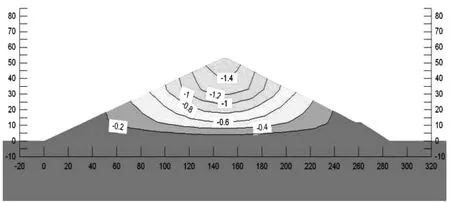
图5 稳定渗流期坝体Y向位移图(单位:m)
表2为静力作用时施工期和稳定渗流期时坝体水平、竖直方向的最大位移。

表2 坝体静力学位移计算
完成坝体的填筑后,如果坚持加坝体自重荷载时,提高时间步这个条件,计算在此之后28个月坝体的沉降值变化,结果见表3。

表3 坝体填筑完成后沉降量计算
通过表3可知,大坝的竖直沉降量在竣工时最大为0.91 m,出现在坝体的河床坝段坝顶处;随着时间的变化坝体沉降也逐渐增大,但增长速率却趋于缓和,完成坝体填筑之后的28个月其沉降值基本稳定,在河床坝段坝顶处,大坝垂直方向最终的沉降值为1.45 m。沉降计算结果表明,坝体在竣工后产生的最大沉降值为0.54 m,是坝体高度的0.99%。沉降结果可以看出,若按照工程经验的1%坝高进行控制,坝顶预留沉降超高可以达到坝体最终沉降的要求。
在上下游两侧坝体的变形基本对称,坝体变形主要以沉陷为主,竖直方向上最大的沉降量是1.45 cm,水平方向上上游坝体的最大位移值是0.515 m、下游坝体的最大位移值是0.257 cm。总的来说,有限元计算的应力分布规律和坝体位移比较合乎常理,现行坝体的设计合理,在蓄水期和竣工期坝体的安全完全能很好的保证。坝体的静力应力应变的计算结果见表4。

表4 坝体静力应力应变计算结果
通过上述计算结果可知,坝体大主应力较规则,呈连续变化趋势,其主要表现在拉应力区没有出现压应力;大主应力也从坝顶至坝底渐渐增加,其应力等值线大致同上游坝坡保持一致;在坝底产生1 520 kPa最大主应力。此外,排水棱体和坝基底部处,因为棱体材料的特性和坝体填筑土的不同,一定程度上发生应力集中现象。坝体大主应力和小主应力的分布规律大体相同,在坝体自身重力荷载的作用之下,压应力成为主导;依然呈现从坝体顶端到坝体底部渐渐增加的趋势,其应力等值线大致与上下游坝坡平行,最大值是675 kPa,但因为浮托力和浸水的作用会导致坝体的上游坝坡有突变。
4 结 论
本文介绍了坝体-坝基体系静力有限元计算和动力反应分析的原理和步骤,采用土体地震反应分析的总应力法,在考虑坝体孔隙水压力的情况下,对均质土坝的算例进行计算,并从静动力位移、大小主应力应变及剪应力应变等方面对计算结果进行分析比较,最终得出坝体内部的液化反应区。主要结论如下:
1)在静力位移计算方面,大坝的竖直沉降量在竣工时最大为0.91 m,出现在坝体的河床坝段坝顶处;随着时间的变化坝体沉降也逐渐增大,但增长速率却趋于缓和,完成坝体填筑之后的28个月其沉降值基本稳定,在河床坝段坝顶处,大坝垂直方向最终的沉降值1.45 m。沉降计算结果表明,坝体在竣工后产生的最大沉降值为0.54 m,是坝体高度的0.99%,若按照工程经验的1%坝高进行控制,坝顶预留沉降超高可以达到坝体最终沉降的要求。
2)在静力应力应变计算方面,坝体大主应力较规则,呈连续变化趋势,其主要表现在拉应力区没有出现压应力;大主应力也从坝顶至坝底逐渐增加,其应力等值线大致同上游坝坡保持一致。
