全转置正交矩阵的几个性质

郭 华

（重庆工商大学数学与统计学院 400067）

1 预备知识

定义2 若实数域上的n阶方阵A，满足AAo=E，则称A为全转置正交矩阵.

由定义可知下列结论显然成立:

引理1 A为全转置正交矩阵的充分必要条件为A－1=AO.

引理2 A为n阶矩阵，则|A|=|AO|.

可得

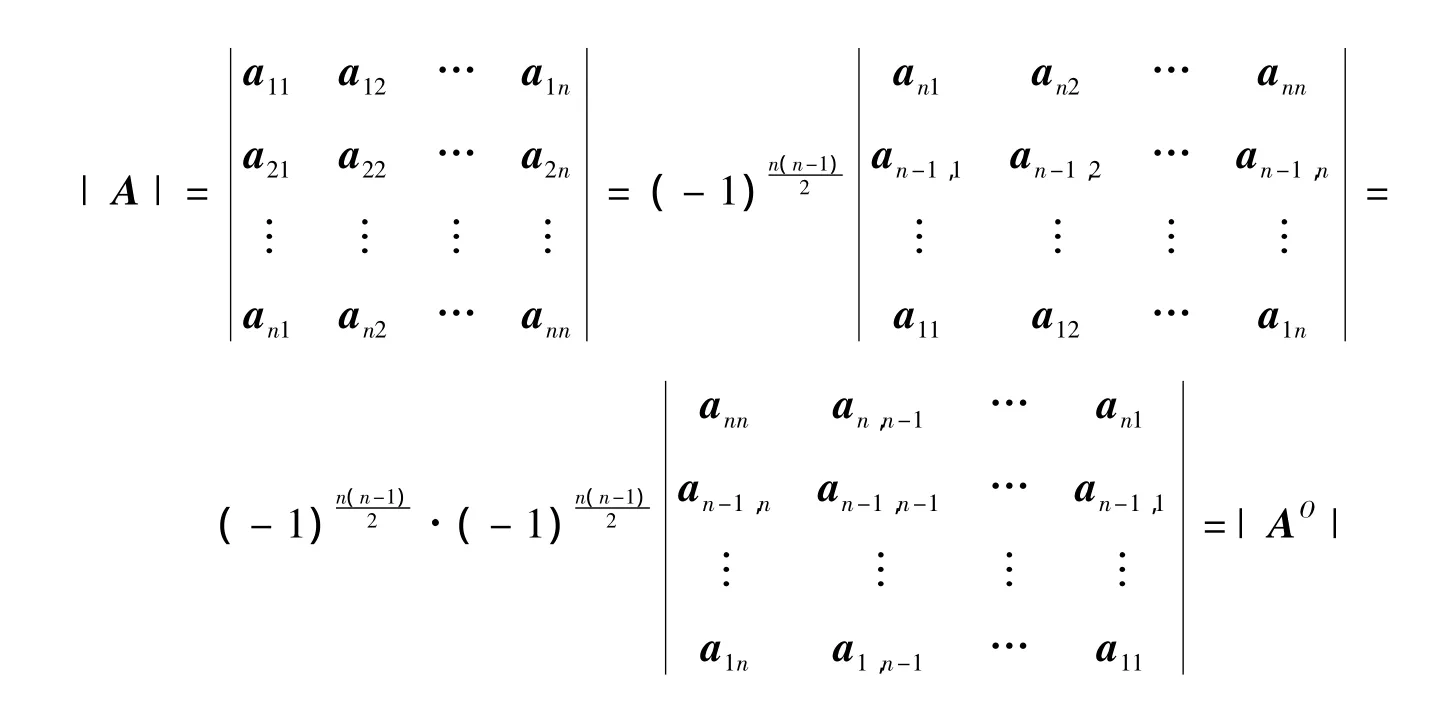
2 3个充要条件

性质1n阶实矩阵A=（aij）是全转置正交矩阵的充要条件为

证明 当A为全转置正交矩阵时，AAO=E，即

由矩阵乘法和比较两端对应元素即得:

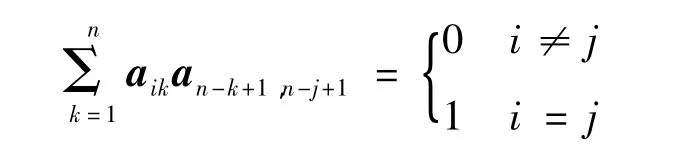
性质2 A为n阶全转置正交矩阵当且仅当|A|=±1，且当|A|=1时，有元素aij的代数余子式Aij=an－j+1，n－i+1，当|A|= －1 时，有元素 aij的代数余子式 Aij= －an－j+1，n－i+1.

证明 “⇒”:因为A为n阶全转置正交矩阵，所以AAO=E，两边取行列式得|AAO|=|E|=1，即|A||AO|=|A|2=1，故|A|= ±1.

当|A|=1时，

由 A－1=AO可得:Aij=an－j+1，n－i+1.同样当|A|= －1，易得 Aij= －an－j+1，n－i+1.

“⇐”:当|A|=1，Aij=an－j+1，n－i+1时，与当|A|= －1，Aij= －an－j+1，n－i+1时，容易得 A－1=AO，所以 A 为全转置正交矩阵.

性质3 对阶数n≥3的实矩阵，A=（aij）是全转置正交矩阵的充要条件为|A|≠0，并当|A|＞0时，有aij=An－j+1，n－i+1;|A|＜0 时，有 aij= －An－j+1，n－i+1（i，j=1，2，…，n）.

证明 “⇒”:注意到

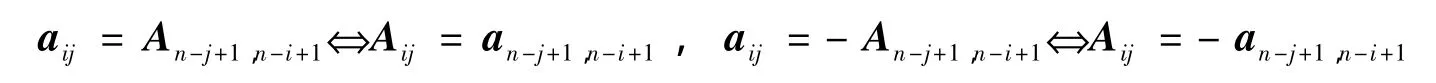
因为 A 是全转置正交矩阵，由性质 2 即知|A|= ±1，且|A|=1 ＞0 时，有 Aij=an－j+1，n－i+1，即 aij=An－j+1，n－i+1;当|A|= －1 ＜0 时，有 Aij= －an－j+1，n－i+1，即 aij= －An－j+1，n－i+1，必要性得证.

“⇐”:当|A|＞0，aij=An－j+1，n－i+1时，只需证明|A|=1 即可.因为此时即有 Aij=an－j+1，n－i+1，于是

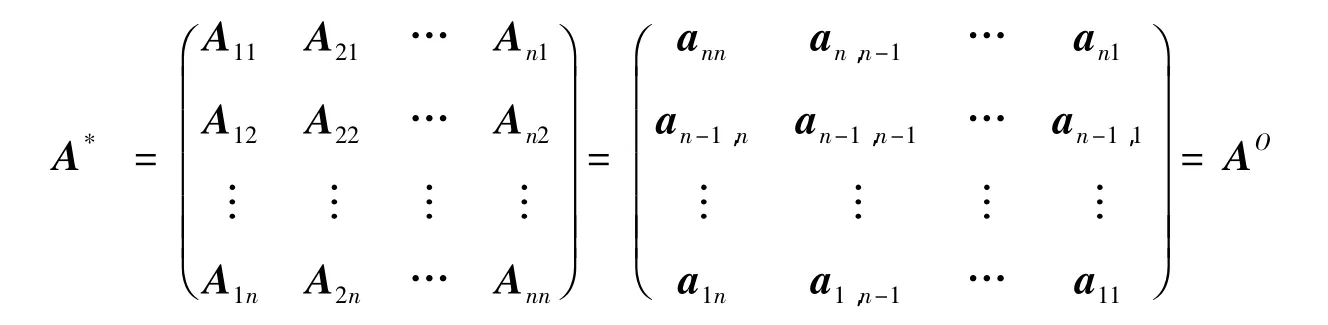
故有 AAO=AA*=|A|E，因为|A|＞0，且|A|=|AO|，所以|A|2=|AAO|=||A|E|=|A|n，于是|A|n－2=1，因n≥3，所以|A|=1，由性质2知A为全转置正交矩阵.

当|A|＜ 0，aij= －An－j+1，n－i+1，同样只需证|A|= －1 即可.此时同样可证 A* = －AO，从而 AAO=－AA*= －|A|E.因为|A|≠0，所以|A|2=|AAO|=|－|A|E|n=（－1）n|A|n，于是|A|n－2=（－1）n故|A|=－1，由性质2知A为全转置正交矩阵.

［1］许永平.旋转矩阵的一些概念与一些结论［J］.江苏广播大学学报，1997（2）:81-84

［2］许永平，石小平.正交矩阵的充要条件与O-正交矩阵的性质［J］.南京林业大学学报:自然科学版，2005（2）:2-4

［3］周素琴.2-旋转矩阵及其性质［J］.上海师范大学学报:自然科学版，2001（1）:89-91

［4］袁晖坪.次正交矩阵与次对称矩阵［J］.西南大学学报:自然科学版，1998（2）:147-150

［5］郭伟.实次规范阵与次正交阵的进一步拓广［J］.重庆工商大学学报:自然科学版，2006（3）:240-242

［6］张枚.高等代数习题选解［M］.浙江:浙江科学技术出版社，1985