一族强单调映射的公共零点的强收敛定理*

唐 艳

（重庆工商大学数学与统计学院，重庆 400067）

设E为一实Banach空间，E*为E的对偶空间，＜·，·＞表示广义对偶对，称J:E→2E*为正规对偶映像，如果:Jx={f*∈E*:＜x，f*＞=‖x‖2=‖f*‖2}，∀x∈E.若E是光滑的，则J是单值的.今后均用j表示单值赋范对偶映射.

设E为一实Banach空间，C为E的一个非空闭凸子集.称映射A:C→C具有L’ipschitz性质，若存在常数L≥0，使得

其中D（A）为A的定义域，R（A）为A的值域.当L＜1时，称A为压缩的;当L=1时，则称A为非扩张的.称A:C→C是强单调的，若存在k＞0使得

式子（1）也可等价表示为

若A是单调的，则方程Ax=0的解与某些进展系统的平衡点相对应.若A是单调的，记A=I－T，则

式子（2）也等价于

令N（A）={x∈D（A）:Ax=0}，F（T）={x∈D（T）:Tx=x}分别表示A的零空间和T的不动点集.显然，A的零点是T=I－A的不动点.

2004年，Chidume［1］在 Banach空间中讨论了迭代过程:

2007 年，Yao［2］在 Banach 空间中证明了序列

的强收敛性，其中Wn是一族非扩张映射.

2009年，Habtu［3］等在Banach空间中固定u，讨论了逆－强粘性映射的零点迭代格式:

2012年，Tang［4］等讨论了一个非扩张映射不动点的粘性迭代格式

的强收敛性.

在此基础上，将构造一个迭代序列强收敛于一族强单调映射的公共零点，相应地，在Banach空间中讨论该强单调映射的公共零点的迭代程序的强收敛性.

1 预备知识

设E为一实Banach空间，K⊂E为闭凸的，若Q（Q（x）+t（x－Q（x）））=Q（x），则称映射Q:E→K为单面的.若Q2=Q，则称Q为缩进的.

此处将在（0，1）中考虑序列{λn}{θn}满足以下条件:

若S={x∈E:‖x‖ =1}为E的单位球面，对任意的

引理1［2］设E是具有一致Gateux可微范数的严格凸的自反Banach空间，K是E的有界闭凸子集，令T:K→K为连续的伪压缩映射，F（T）≠Ø.对u∈K，映射yt∈K，t∈（0，1］满足yt=（1 －t）Tyt+tu，则yt在t→0+时强收敛于T的不动点Qu，其中Q:K→F（T）是唯一的单面非扩张缩进.

引理2［3］设E为一实Banach空间，E*为E的对偶空间，J:E→2E*为正规对偶映像，则对任意的x，y∈E，有‖x+y‖2≤‖x‖2+2 ＜y，j（x+y）＞，∀j（x+y）∈J（x+y）.

2 主要结果

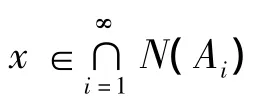
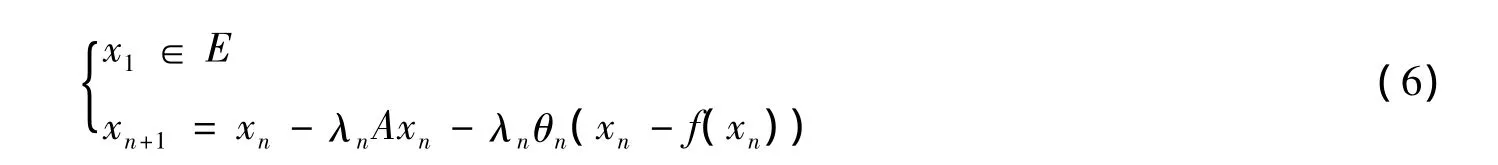
证明 首先说明{xn}的有界性.令∀p∈N（A），则Ap=0，且由A的强单调性可知，

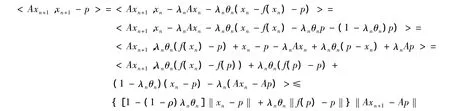
由于{yn}可以表示为

由引理2可知

因为θn（f（xn）－yn）－Ayn=0，且由A的强单调性可知＜Axn+1－Ayn，j（xn+1－yn）＞≥0，所以式（8）可以表示为

由于N（A）≠Ø，由文献［3］的性质2可知{yn}有界，因此存在M＞0，使得max{（θn+2）‖Axn+θn（xnf（xn））‖，‖xn+1－yn‖}＜M，则式（9）可以表示为

另外再由算子A的强单调性以及对偶映射的性质可知

由式（10）和式（11），以及{yn}{f（xn）}的有界性可知

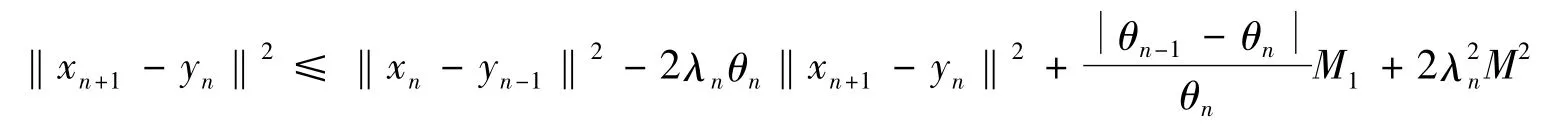
其中M1＞0为一常数.则由引理3和{λn}{θn}的条件可知，xn+1－yn→0.所以n→∞时，‖xn－yn‖→0，由引理1 可知yn→y=Qξ∈N（A），从而{xn}强收敛于{A1，A2，…}的公共零点Qξ.

［1］REICH.Strong convergence theorems for resolvents of accretive operators in Banach spaces［J］.Math Anal App，1980（75）:287－292

［2］CHIDUME C E，ZEGEYE H，ANEKE S J.Strong convergence theorems for a finite family of nonexpansive mappings in Banach spaces［J］.Comm Appl NonliearAnal，2004，11（2）:25－32

［3］YAO Y，YAO J C，ZHOU H.Approximation methods for common fixed point of infinite countable family of nonexpansive mappings［J］.Comput Math Appl，2007（53）:1380－1389

［4］ZEGEYE H，SHAHZQAD N.Strong convergence theorems for a common zero of a countably infinite family of α－inverse strongly accretive mappings［J］.Nonliear Anal，2009（71）:531－538

［5］唐艳.Banach空间中非扩张映射不动点的粘性逼近［J］.重庆工商大学学报:自然科学版，2012，29（1）:1－3

［6］闻道君.混合拟变分不等式的预测－校正算法［J］.西南师范大学学报:自然科学版，2009，34（5）:41－44