一类非线性抛物方程解的爆破时间估计*

王勤锋，周寿明

（重庆大学数学与统计学院，重庆 401331）

非线性抛物方程解的爆破现象在过去几十年内已经得到了很多人的关注，在文献［1－7］中，他们研究了一些线性抛物方程解的全局存在、局部存在、解的爆破、爆破速率、爆破集、爆破时间上界估计.然而，比较难得到爆破时间的一个下界估计.

在2008年，Payne，Philippin和Schaefer等人在文献［8］中考虑了下列一类带有齐次边界条件方程解的爆破现象

当ρ是一个C1函数，而且满足

他们得到了爆破时间的一个下界估计.

进一步，在2009年，Li，Liu和Lin在文献［10］中考虑了问题（1）的第三界边界条件

并且给出了爆破时间的一个下界估计以及非爆破条件.

在2011年，Li，Liu和Xiao在文献［11］中研究了下列带有第三界边界条件的方程

容易验证在方程（4）中，ρ（|▽u|2）=|▽u|p+1并不满足Payne等人在研究这类方程时所限制的条件（2），但作者依然得到了爆破时间的一个下界估计.受上述工作的启发，讨论下面一类非线性抛物方程的爆破时间的下界估计

其中 Ω⊂R3为带有光滑边界的有界凸区域，0≤m≤1，k＞0，函数f（x）满足0＜f（s）≤a1+a2sq，s＞0，a1＞0，a2＞0.

1 主要结果

定理2 如果u（x，t）是方程（5）的解，且q－1－p＜0，则u（x，t）不会在有限时间内爆破.

2 主要结果及证明

下面给出定理1和定理2的证明，首先给出定理1的证明，之后证明定理2.

定理1的证明

证明 对φ求导，有

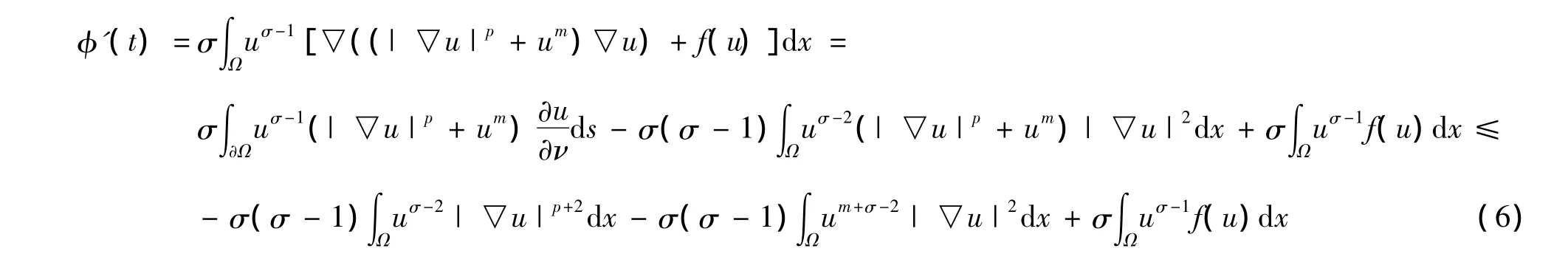
再由f的限制条件及|▽un|2=n2u2n－2|▽u|2，有

其中|Ω|是Ω的体积，设v=un，故

由Poincare不等式

其中λ1是问题（11）的第一正的特征值.

可以得到

由于Ω是凸集，可定义

则式（13）可转化为

θ＞0，联合式（12）和式（15），则有

在这里限制凸集Ω满足

其中，联合式（8）和式（18）有

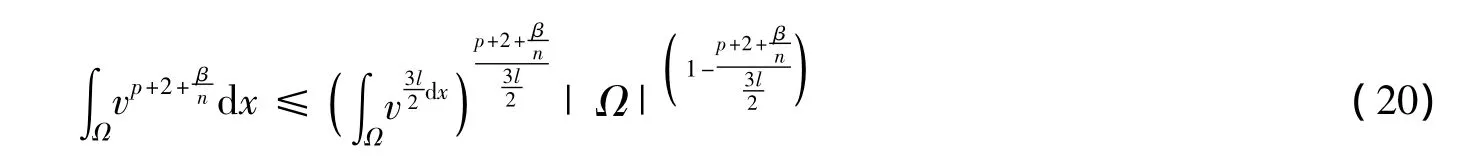
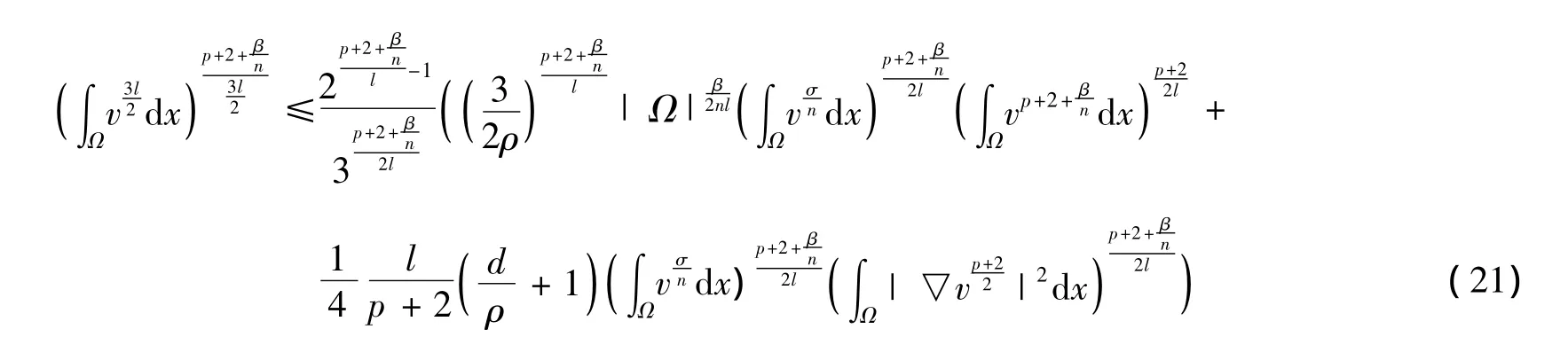
运用不等式arbs≤ra+bs，r+s=1，a，b＞0. 由式（20）和（21），得到

在这里

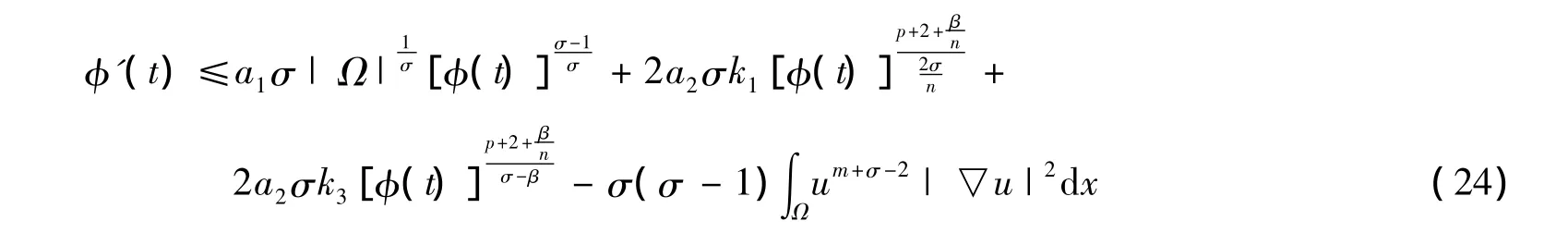
其中λ0是问题（26）的第一特征值.

把式（27）代入式（24），得到

若u（x，t）在有限时间T发生爆破，对式（29）两边积分可得

定理1证毕，下面给出定理2的证明.

定理2的证明

证明 设Φ（t）=∫Ωu2dx，对Φ（t）两边求导有

类似于前面的讨论，

因p+1＞q，所以

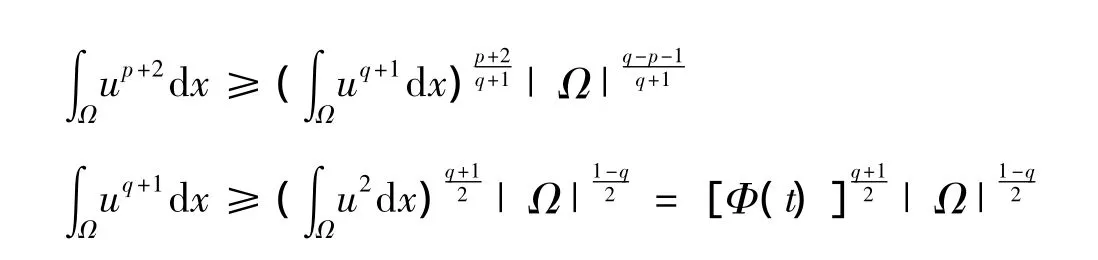
所以

容易看出，如果u（x，t）在有限时间爆破，由式（34）和式（36）可以得出Φ'（t）≤0，这是矛盾的.定理2证毕.

［1］FRIEDMAN A，MCLEOD B.Blow－up of positive solutions of semilinear heat equations［J］.Indiana Univ Math，1985（34）:425－447

［2］CAFFARRELLI A，FRIEDMAN A.Blow－up of solutions of nonlinear heat equations［J］.Math Anal Appl，1988（129）:409－419

［3］PAYNE L E，SCHAEFER P W.Lower bounds for blow－up time in parabolic problems under Dirichlet conditions［J］.Math Anal Appl，2007（328）:1196－1205

［4］GALAKTIONOV V A，VAZQUEZ J L.The problem of blow up in nonlinear parabolic equations［J］.Discrete Contin Dyn Syst，2002（8）:399－433

［5］BALL J M.Remarks on blow up and nonexistence theorems for nonlinear evolution equations［J］.Quart Math Oxford，1977（28）:473－486

［6］FRIEDMAN A.Remarks on the maximum principle for parabolic equations and its applications［J］.Pacific Math，1958（8）:201－211

［7］BANDLE C，BRUNNER H.Blow－up in diffusion equations［J］.Comput Appl Math，1998（97）:3－22

［8］PAYNE L E，PHILIPPIN G A，SCHAEFER P W.Blow－up phenomena for some nonlinear parabolic problems［J］.Nonlinear Anal，2008（69）:3495－3502

［9］PAYNE L E，PHILIPPIN G A，SCHAEFER P W.Bounds for blow－up time in nonlinear parabolic problems［J］.Math Anal Appl，2008（338）:438－447

［10］LI Y F，LIU Y，LIN C H.Blow－up phenomena for some nonlinear parabolic problems under mixed boundary conditions［J］.Nonlinear Anal RWA，2010（11）:3815－3823

［11］LI Y F，LIU Y，XIAO S Z.Blow－up phenomena for some nonlinear parabolic problems under Robin boundary conditions［J］.Math Comp Mode，2011（54）:3065－3069

［12］袁幼成，周宗福，周辉.一类分数阶微分方程共振边值问题解的存在性［J］.重庆工商大学学报:自然科学版，2012（3）:1－6