非自治常微分方程组周期解的存在性*
2013-05-28张申贵
张申贵
(西北民族大学数学与计算机科学学院,甘肃兰州 730030)
则问题
使得
则问题(1)在Sobolev空间H1T中至少有一个周期解.
注:式(2)表明非线性项▽F(t,u(t))是线性增长的.
定理1和2中要求式(3)中极限值为+∞,即Ahmad-Lazer-Paul型强制性条件成立.易见式(3)中极限值可以是下方有界的,极限值的范围从+∞放宽为
在Sobolev空间上定义泛函φ如下:
则φ弱下半连续且连续可微,u∈H1T是问题(1)的周期解当且仅当u是泛函φ的临界点.
引理1[3] (极小作用原理)若泛函φ:X→R弱下半连续,且φ在自反Banach空间X中强制,即当‖u‖→∞时,有φ(u)→+∞,则泛函φ在空间X中有极小值.
考虑非自治常微分方程组
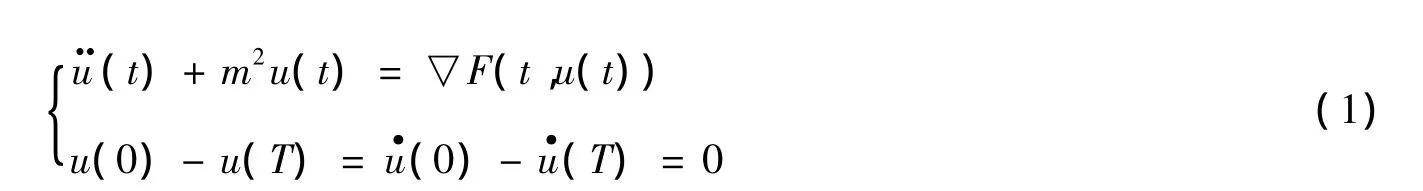
其中T>0,F:[0,T]×RN→R 满足:对∀x∈RN,F(t,x)可测,对 a·e·t∈[0,T],F(t,x)连续可微;且存在a∈C(R+,R+),b∈L1(0,T;R+),使得
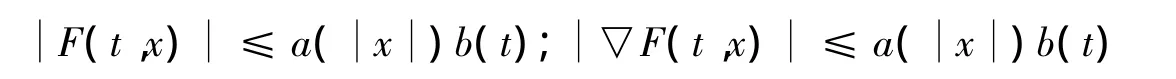
许多数学模型都可以归结为非自治常微分方程组.近年来,非自治常微分方程组周期解的存在性成为了人们研究的重要课题[1-6].
当m=0时,文献[1]得到了下面定理:
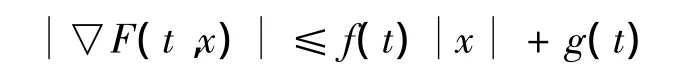
对所有x∈RN和a·e·t∈[0,T]成立,且F满足Ahmad-Lazer-Paul型强制性条件
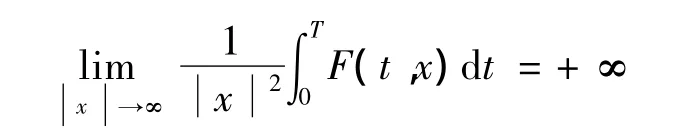
则问题
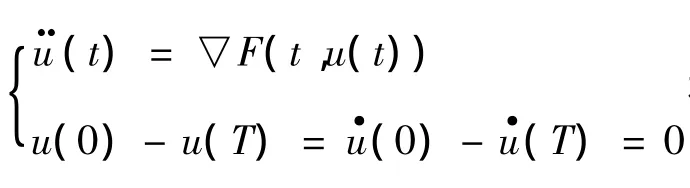
当m不恒等于0时,文献[2]得到了下面定理:
使得

对所有x∈RN和a·e·t∈[0,T]成立,且F满足Ahmad-Lazer-Paul型强制性条件
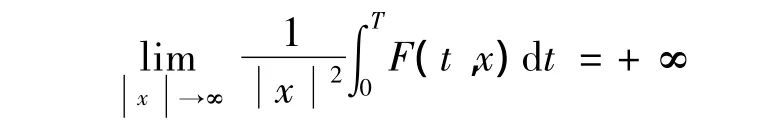
则问题(1)在Sobolev空间H1T中至少有一个周期解.
定理3 设F满足式(2)且
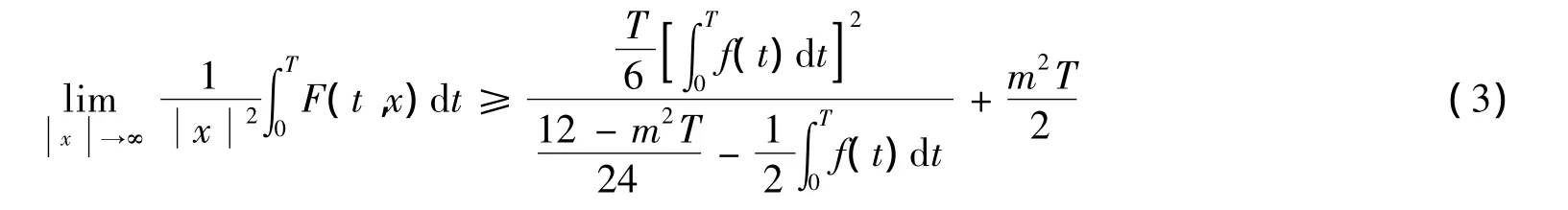
则问题(1)在Sobolev空间H1T中至少有一个周期解.
注:式(2)表明非线性项▽F(t,u(t))是线性增长的.
定理1和2中要求式(3)中极限值为+∞,即Ahmad-Lazer-Paul型强制性条件成立.易见式(3)中极限值可以是下方有界的,极限值的范围从+∞放宽为
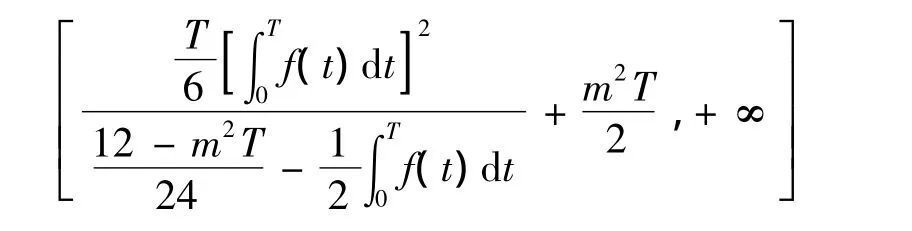
定理1对应于定理3中m=0,且式(3)中极限值为+∞的特殊情形.
定理2对应于定理3中式(3)中极限值为+∞的特殊情形.
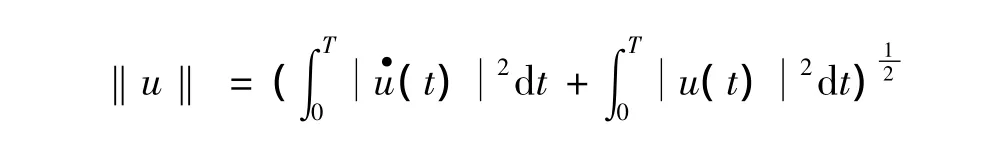
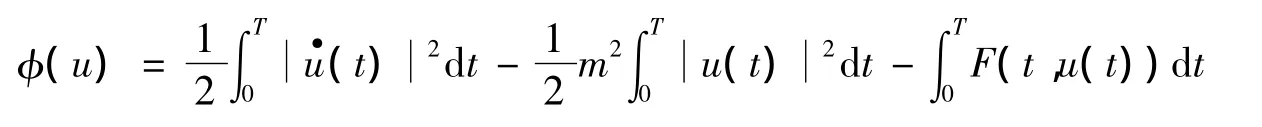
则φ弱下半连续且连续可微,u∈H1T是问题(1)的周期解当且仅当u是泛函φ的临界点.
引理1[3](极小作用原理)若泛函φ:X→R弱下半连续,且φ在自反Banach空间X中强制,即当‖u‖→∞时,有φ(u)→+∞,则泛函φ在空间X中有极小值.
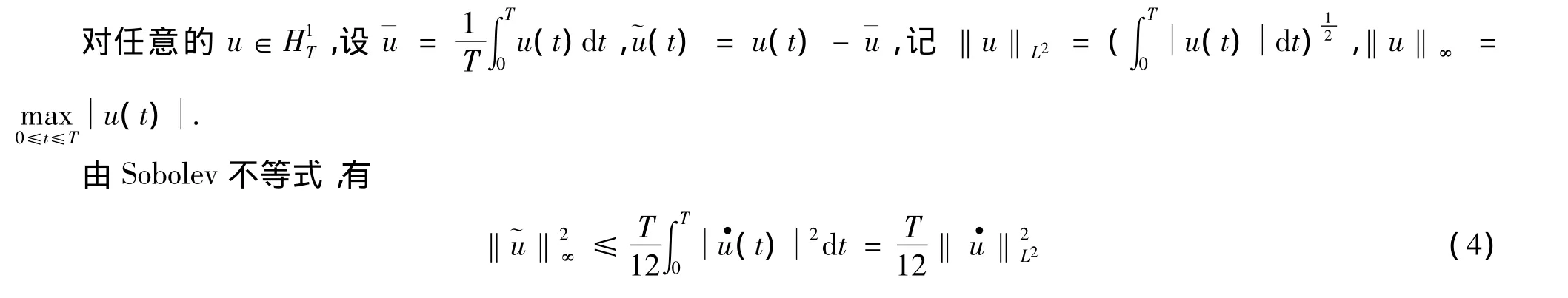
定理3的证明
由式(2)和式(4)、均值不等式,有
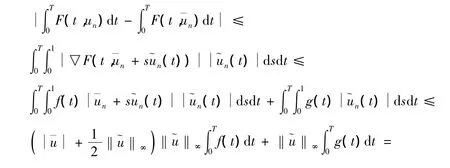
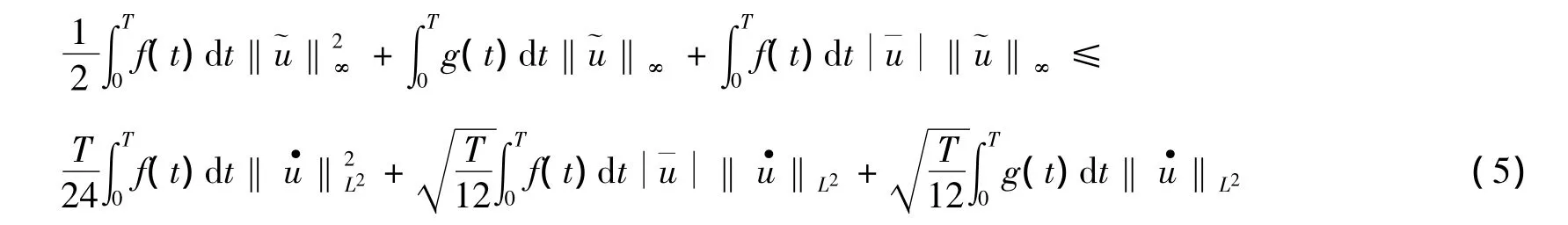
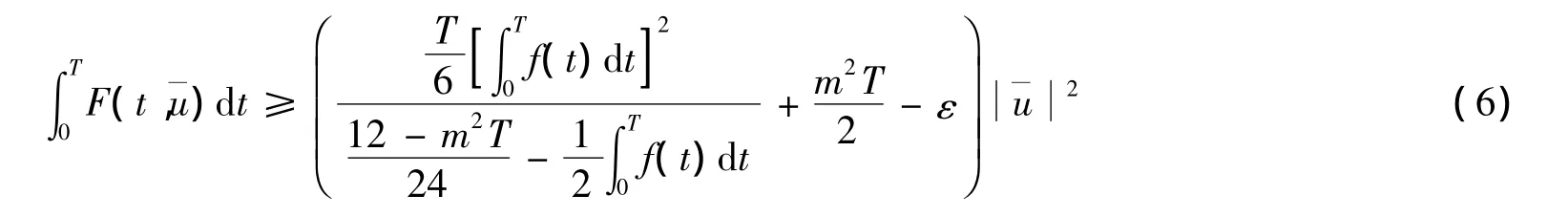
由式(5)(6),有
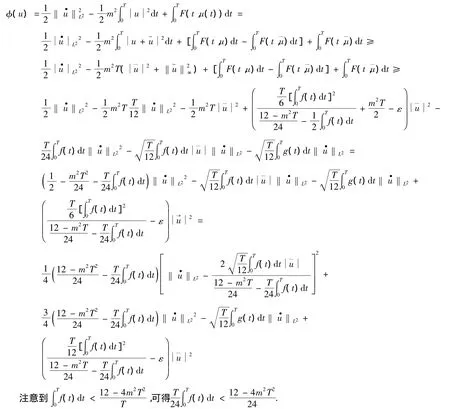
[1]ZHAO F K,WU X.Existence of periodic solutions for nonautonmous second order systems with linear nonlinearity[J].Nonlinear Anal,2005,60(7):325-335
[2]王少敏,冷天玖.关于常微分方程组周期解的存在性定理[J].重庆工商大学学报:自然科学版,2007(2):119-121
[3]MAWHIN J,WILLEM M.Critical point theory and Hamiltonian systems[M].NewYork:Springer-Verlag,1989
[4]韩志清.共振条件下的常微分方程组2π-周期解的存在性[J].数学学报,2000(4):639-644
[5]王少敏.带有阻尼项的二阶哈密顿系统的周期解[J].重庆工商大学学报:自然科学版,2011(4):6-11
[6]HAN Z Q.Existence of periodic solutions of linear Hamiltonian systems with sublinear perturb-ation[J].Boundary Value Probiems,2010(12):123-131
