不定方程y2=x3－13的初等解法

熊 军，敬 勇

（1.重庆育才中学，重庆400050;2.西南财经大学数学系，成都 610074）

利用代数数论知识［1－2］，易知不定方程

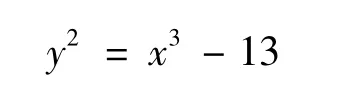
仅有解x=17，y=±70.下面避开代数数论，给出它的初等解法.

先作一些准备工作.考察不定方程

其中n∈Z+，n＞13 并且（n，13）=1.

若{x1，y1}为式（1）的解，满足（x1，y1）=1，则称{x1，y1}为式（1）的本原解.

引理1 若式（1）有本原解，则同余方程

有解.

证明 令{x1，y1}是式（1）的一组本原解，则（x1y1，n）=1，于是同余方程

有解，因此S2y21≡x21≡－13y2（modn），从而S2≡－13（modn）.引理1证毕.

引理2 令m＞1，（a，m）=1，则二元一次同余方程

必有解u0，v0，满足

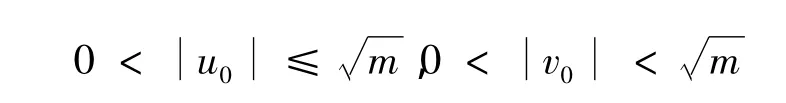
证明 考虑集合au+v，u的取值范围是

v的取值范围是

则这个集合的元素个数是

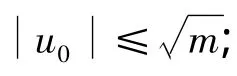
引理3 若式（2）有解S1（modn），则不定方程（1）有一组本原解{x1，y1}，满足

证明 显然有（S1，n）=1，因而由引理2知，必有u0，v0满足

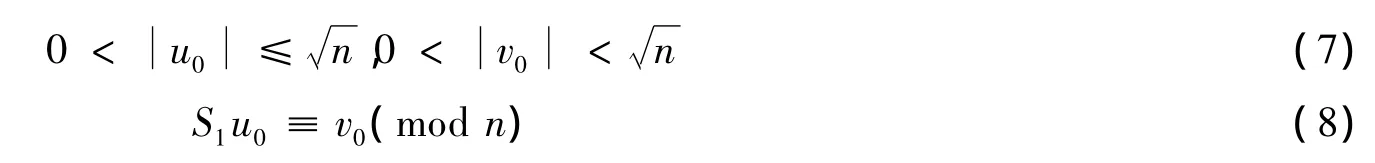
若k=2，则式（1）无解.若式（1）有解，考虑方程组

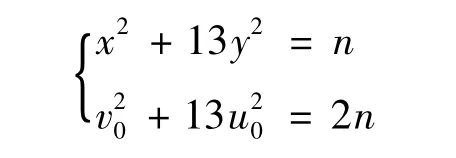
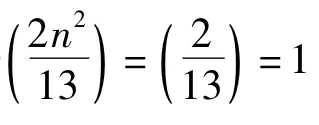
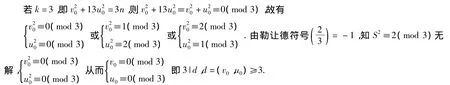
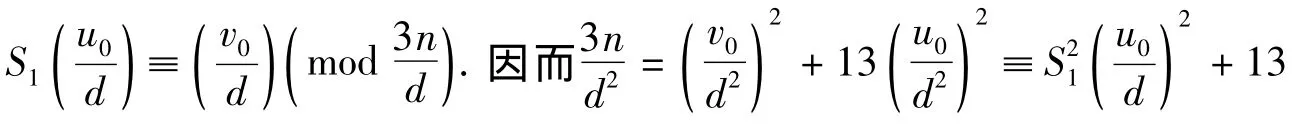
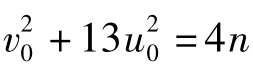
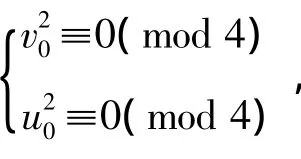
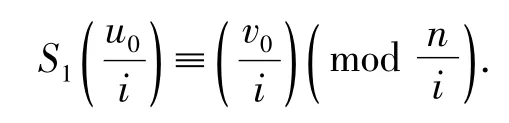
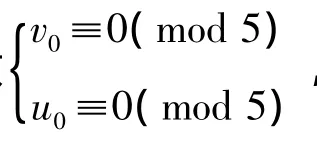
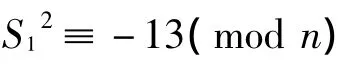
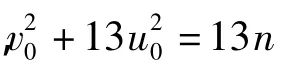
若{x1，y1}，{x2，y2}是式（1）的两组不同的非负本原解，满足

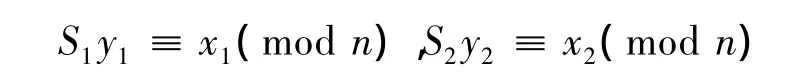
则S2±S1不同余.

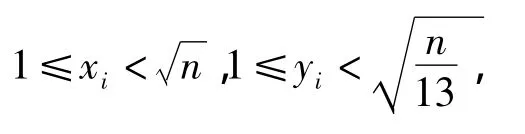
由（x1，y1）=（x2，y2）=1，即得x1=x2，y1=y2，矛盾.

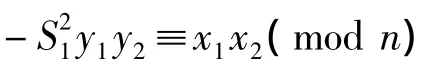
因1≤13y1y2，x1x2＜n，故13y1y2=x1x2，于是13|x1x2.但（x1，13）=1，（x2，13）=1，故（x1x2，13）=1，矛盾.

由此可得，若{x0，y0}为式（1）的一组非负本原解，则对应着式（2）的一对解±S1（modn）.反之，若±S1（modn）为式（2）的一对解，则对应着式（1）的一组非负本原解{x0，y0}.所以式（1）的非负本原解数是式（2）的解数的一半.

定理1 不定方程（1）的非负本原解数是

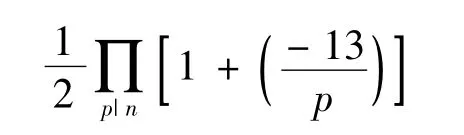
由于n∈Z+，n＞13并且（n，13）=1，因此式（1）的非负本原解必为正解，于是有推论1.

推论1 不定方程（1）的本原解数是其非负本原解数的4倍，即是

下面来考察不定方程

其中n∈Z+，（n，13）=1.

若{a，b}为式（11）的本原解，则n3=（a2+13b2）3=a6+3×13a4b2+3×132a2b4+133b6.配方得n3=（a3－39ab2）2+13（3a2b－13b3）2.

因为（a，b）=1，必有（a，2b）=1，故（a3－39ab2，3a2b－13b3）=1，于是式（10）有一组本原解{a3－39ab2，3a2b－13b3}.令式（10）和（11）的本原解之集分别为S和T，在S和T之间建立映射f如下:

则称f是单射.令

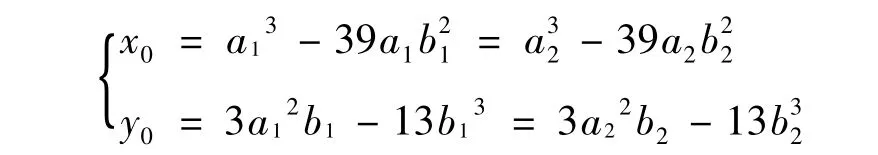
这时{a1，b1}，{a2，b2}∈S，故{x0，y0}∈T，于是方程

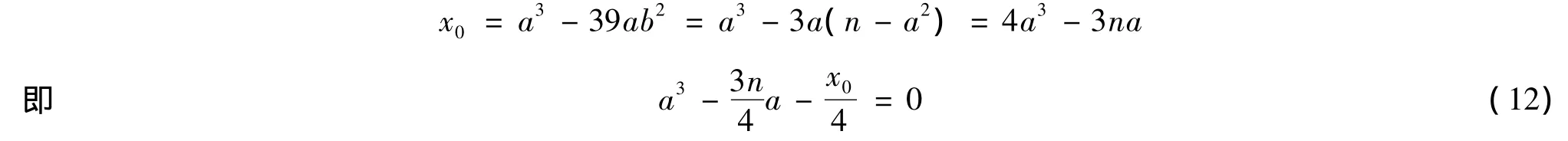
有两个有理根a1和a2.但式（12）的判别式

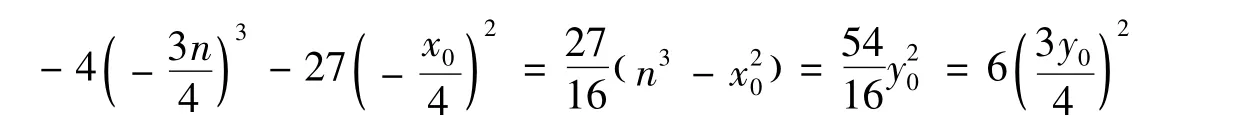
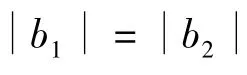
定理2 不定方程（10）的本原解为x=a3－39ab2，y=3a2b－13b3，其中{a，b}为式（11）的本原解，（a，2b）=1.

显然，n=1时，式（10）和（11）的解均为{±1，0}，仍可归结为表达式（12）.

推论2 不定方程x2+13y2=z3的本原解为

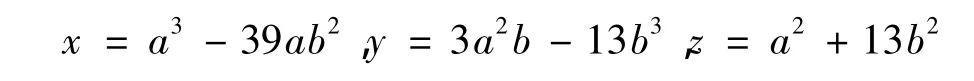
这里（a，2b）=1.

定理3 不定方程y2=x3－13仅有解x=17，y=±70.

证明 把y2=x3－13改写为y2+13×12=x3，显然（x，y）=1.由推论（2），得

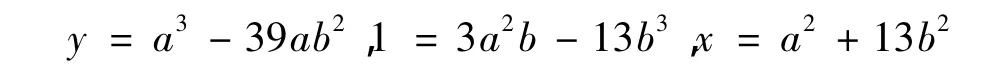
得a= ±2，b= －1，故x=17，y= ±70.

［1］李伟.不定方程y3=x2+2的初等解法［J］.四川大学学报:自然科学版，1997，34（1）:16－19

［2］潘承洞，潘承彪.初等数论［M］.北京:北京大学出版社，1992